
第5章 风刚体力学基础 APACHE
第 5 章 刚体力学基础

第5章风刚体力学基出 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.1刚体运动的描述 刚体:既考虑物体的质量,又考虑形状和大小,但忽 略其形变的物体模型。 刚体可看作是质量连续分布的且任意两质量元之间 相对距离保持不变的质点系。 一、刚体运动的基本形式 1.平动 列体内任一直线在运动过程中始终保持平行。 刚体内各质点在任一时刻具有相同的速度和加速度。 >可以用质点动力学的方法来处理刚体的平动问题
刚体:既考虑物体的质量, 又考虑形状和大小,但忽 略其形变的物体模型。 刚体可看作是质量连续分布的且任意两质量元之间 相对距离保持不变的质点系。 §5.1 刚体运动的描述 一、刚体运动的基本形式 ¾ 可以用质点动力学的方法来处理刚体的平动问题。 刚体内各质点在任一时刻具有相同的速度和加速度。 1. 平动 刚体内任一直线在运动过程中始终保持平行

2.转动 刚体上所有质点都绕同一直线(即转轴)作圆周运动。 a.定轴转动 如:门、窗的转动等。 b.定点转动 如:陀螺的转动。 3.平面运动 列体上每一质元的运动都平行于某一固定平面。 可以分解为刚体随质心的平移和绕质心垂直于运动平 面的定轴转动。如:车轮滚动。 4.刚体的一般运动 可以分解为随质心的平移和绕质心的定点转动
a. 定轴转动 b. 定点转动 如:门、 窗的转动等。 如:陀螺的转动。 3. 平面运动 可以分解为刚体随质心的平移和绕质心垂直于运动平 面的定轴转动。如:车轮滚动。 刚体上每一质元的运动都平行于某一固定平面。 可以分解为随质心的平移和绕质心的定点转动。 4. 刚体的一般运动 刚体上所有质点都绕同一直线(即转轴)作圆周运动。 2. 转动
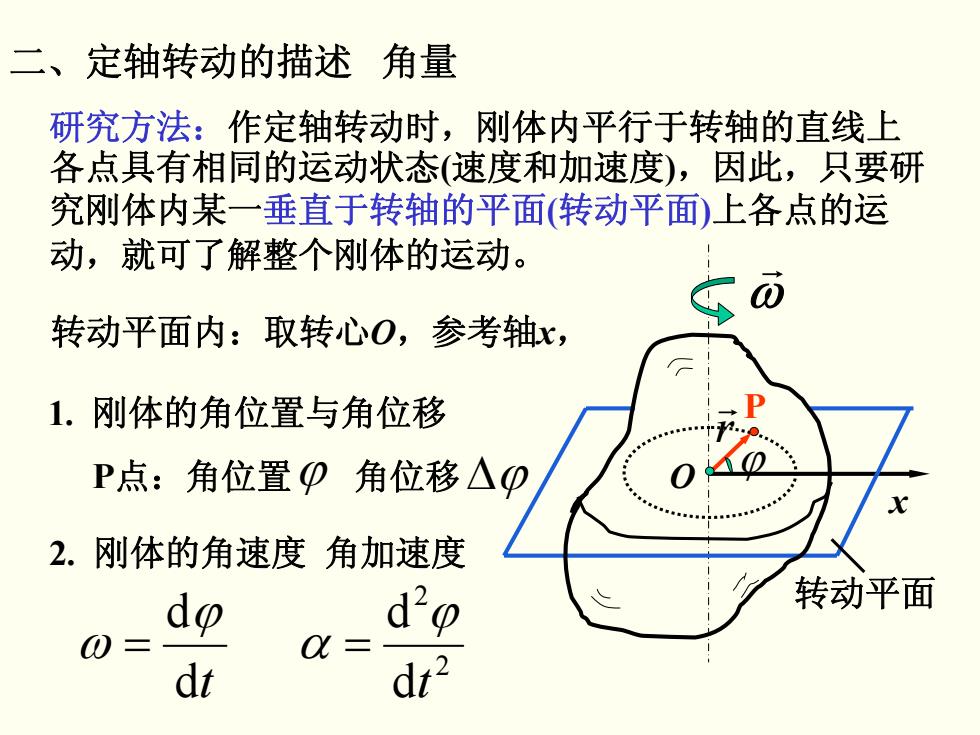
二、定轴转动的描述 角量 研究方法:作定轴转动时,刚体内平行于转轴的直线上 各点具有相同的运动状态(速度和加速度),因此,只要研 究刚体内某一垂直于转轴的平面(转动平面)上各点的运 动,就可了解整个刚体的运动。 转动平面内:取转心O,参考轴x, 1.刚体的角位置与角位移 P点:角位置p角位移△0 2.刚体的角速度角加速度 do 转动平面 0= X= dt dt2
研究方法:作定轴转动时,刚体内平行于转轴的直线上 各点具有相同的运动状态(速度和加速度),因此,只要研 究刚体内某一垂直于转轴的平面(转动平面)上各点的运 动,就可了解整个刚体的运动。 转动平面内:取转心O,参考轴x, 1. 刚体的角位置与角位移 2. 刚体的角速度 角加速度 dt dϕ ω = 二、定轴转动的描述 角量 x O P r r ϕ ω r 转动平面 2 2 d d t ϕ α = P点:角位置 角位移 ϕ Δϕ
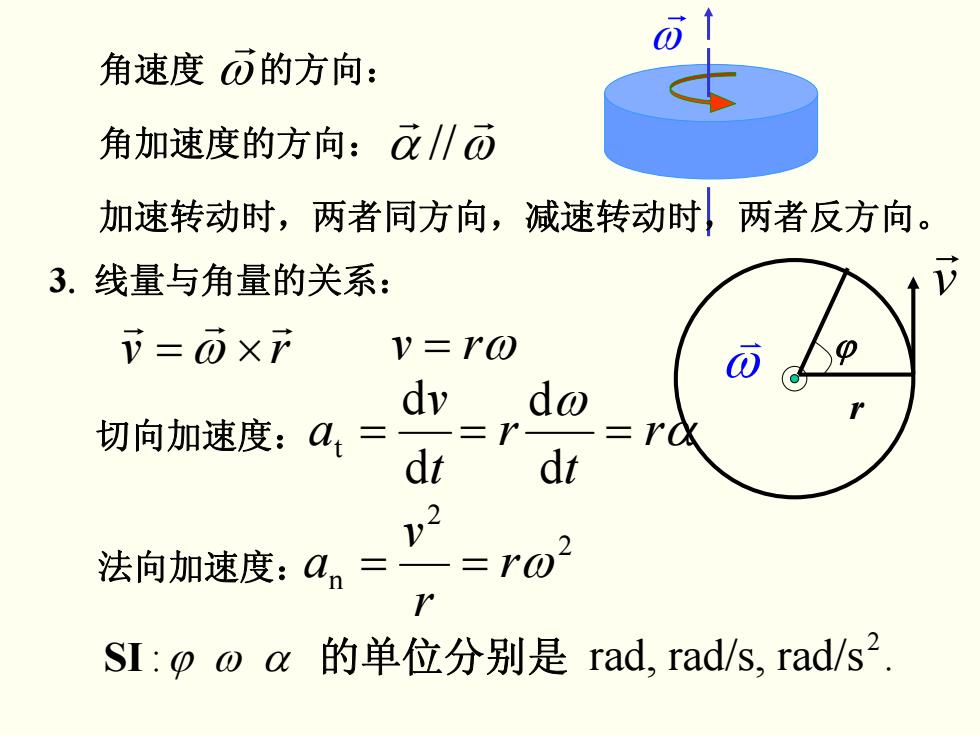
角速度ō的方向: 角加速度的方向:/ō 加速转动时,两者同方向,减速转动时两者反方向。 3.线量与角量的关系: 币=而XF v=ro dv do 切向加速度:at= dt dt 2 法向加速度:an= =r0 SI:poa的单位分别是rad,rad/s,rad/s2
3. 线量与角量的关系: :ϕ ω α SI 的单位分别是 .rad/srad/s,rad, 2 rv r r r ω ×= = rv ω 角速度 的方向: ωr ω r r ϕ v r ω v α ω r r 角加速度的方向: // 加速转动时,两者同方向,减速转动时,两者反方向。 t v a d d t = α ω r t r == d d 切向加速度: 2 2 n rω r v 法向加速度:a ==

对于匀角加速转动,则有: 匀加速直线运动: 0=00+0t v=vo +at 1 0=p0+0t+。at2 x=xo+vot+at2 2 o2-m=2a(0-p)v2-=2a(x-x) 式中:0o,p0是t=0时刻的角速度和角位置。 说明:作定轴转动时,刚体内各点具有相同的角量, 但不同位置的质点具有不同的线量。 END
对于匀角加速转动,则有: ω =ω +αt 0 2 00 2 1 ++= αωϕϕ tt )(2 0 20 2 −=− ϕϕαωω 式中: 00 ω , ϕ 是 t =0 时刻的角速度和角位置。 说明:作定轴转动时,刚体内各点具有相同的角量, 但不同位置的质点具有不同的线量。 匀加速直线运动: )(2 2 1 0 2 0 2 2 00 0 xxavv attvxx atvv −=− ++= = + END