
第5章刚体力学基出 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动
5 E §5.5 刚体定轴转动的功能原理 刚体定轴转动的转动动能 E-∑4m-∑Awm听o=2a 由平行轴定理:J=J+md1 E-北.+m-2/w2w 2 -mv >定轴转动可分解为刚体绕过质心轴的转动和随质心 (绕定轴作圆周运动)的平动
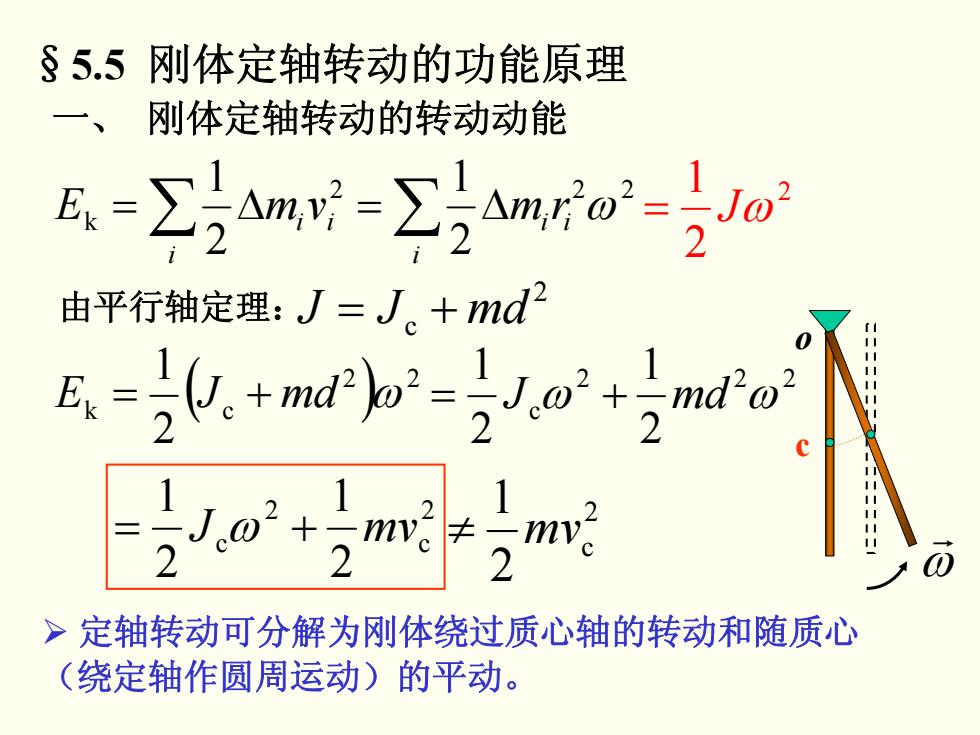
一、 刚体定轴转动的转动动能 ∑ ∑ Δ=Δ= i i ii ii E vm rm 2 22 k 2 1 2 1 ω 2 c += mdJJ ( ) 22 k c 2 1 += mdJE ω 2 c 2 c 2 1 2 1 ω += mvJ ¾ 定轴转动可分解为刚体绕过质心轴的转动和随质心 (绕定轴作圆周运动)的平动。 2 2 1 = Jω 2 c 2 1 ≠ mv §5.5 刚体定轴转动的功能原理 o c ω r 由平行轴定理: 2 22 c 2 1 2 1 ω += mdJ ω

二、力矩的功 A=∑A,A=∫(月+∑f)d近 说明 1.平行于定轴的外力对质元不做功。 2.由于刚体内两质元的相对距离不d日 变,一对内力做功之和为零。 dA,=f·d=0 “=房+dd1(f)
二、力矩的功 1. 平行于定轴的外力对质元不做功。 2. 由于刚体内两质元的相对距离不 变,一对内力做功之和为零。 ijijij rfA r r ⋅= dd = ∑ i AA i ∫ ∑ ⋅+= ≠ i ij i i ij rfFA r r r d)( ijijij rrr r r r Q += d frr ijijij )(d r r r ⊥∴ 说明 r r i j i r r d j r r d ijij rr r r + d ij r r d i j =0

设作用在质元△m,上的外力F,位于转动平面内。 d4,=F·df=F,cosO,ds, =F;sina,rdo,=M,do 合外力对刚体做的元功: 竖鬼 dM=∑d4=∑M,dp=Mdo 力矩的功: A-f"Mdo 功率: P、 dA =Mdo=Mo dt dt
iiiiii =⋅= θ dcosdd sFrFA r r = M i dϕ 合外力对刚体做的元功: ∑ == ∑i i i dd i MAA dϕ ∫ = ϕ ϕ ϕ 0 力矩的功: MA d 功率: t A P d d = z P r ri r Fi dϕ θ i s r d αi 设作用在质元 Δ m i上的外力 位于转动平面内。 Fi r iiii = α rF dsin ϕ = Mdϕ ω ϕ M t M == d d

三、刚体定轴转动的动能定理 M=Jdo =jdo do=Jo do dt do dt 2 合外力矩对刚体所作的功等于刚体转动动能的增量
三、刚体定轴转动的动能定理 t JM d d ω = 2 0 2 2 1 2 1 dd 0 0 ωωωωϕ ω ω ϕ ϕ == −= JJJMA ∫∫ 合外力矩对刚体所作的功等于刚体转动动能的增量。 ϕ ω ω ϕ ϕ ω d d d d d d J t = J =
四、刚体的重力势能 以地面为势能零点,刚体和地球 系统的重力势能: E,=∑Am8, △m,8 =s mgzc 2、为物体质心的2坐标
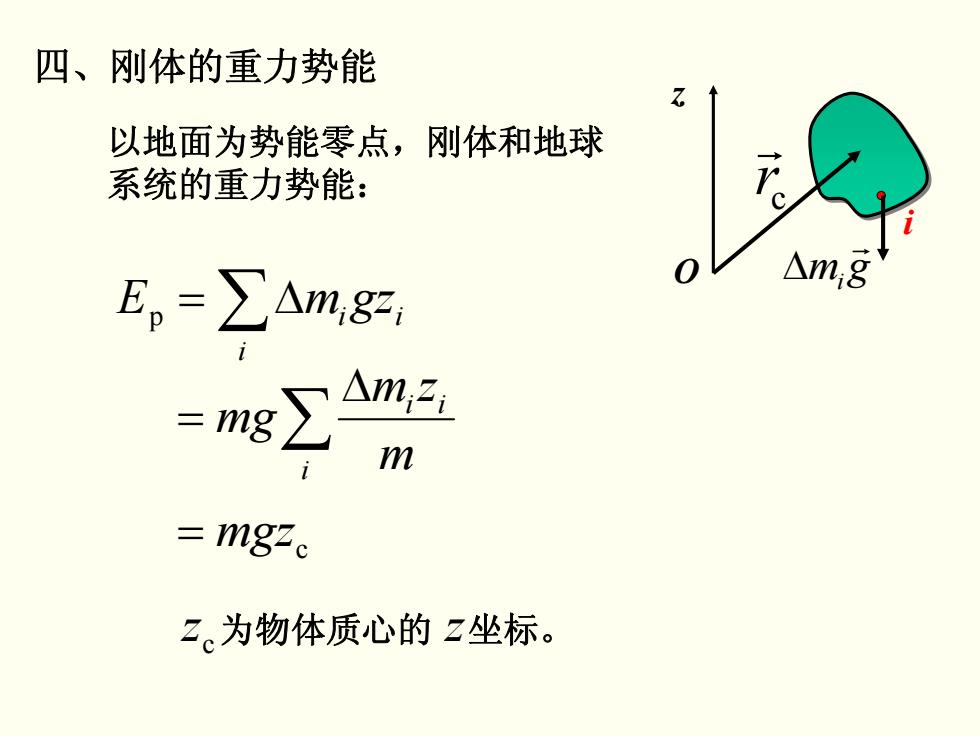
四、刚体的重力势能 以地面为势能零点,刚体和地球 系统的重力势能: ∑Δ= i ii p gzmE igm r Δ z O i cr r ∑ Δ = i ii m zm mg = mgz c c z 为物体质心的 坐标。 z

五、刚体定轴转动的功能原理 J01 J0 2 2 2 将重力矩作的功用重力势能差表示: Md-(mg.-mga) 得 Md-(mg-.+Jo)-(mgz.+J) 刚体定轴转动的功能原理 其中,M是除重力以外的其它外力的合力矩。 若M-0,则mg。+万Jo2=常量 刚体的机械能守恒定律
五、 刚体定轴转动的功能原理 将重力矩作的功用重力势能差表示: (d ) p c 0c 0 M −−= mgzmgz ∫ ϕ ϕ ϕ 得 ) 2 1 () 2 1 (d 2 0c 0 2 c 0 ϕ ω ω ϕ ϕ∫ +−+= JmgzJmgzM 其中, M是除重力以外的其它外力的合力矩。 ——刚体的机械能守恒定律 2 0 2 2 1 2 1 −= JJA ωω ——刚体定轴转动的功能原理 若 M=0,则 c 2 =+ 常量 2 1 Jmgz ω
[例5-15]均质细棒m,1,水平轴0,开始棒处于水平状 态,由静止释放,求棒摆到竖直位置时:()棒的角速度, (2)棒的转动动能,(3)质心的加速度,(4)轴对杆的支反力。 解: 二mg2= 3g (1) Jo y 2 (2) Ek 2 2=1mg2 3 3) 8 (4)Fs mdet =0 F,-mgmgmg 5 Fy-mg=mdcn
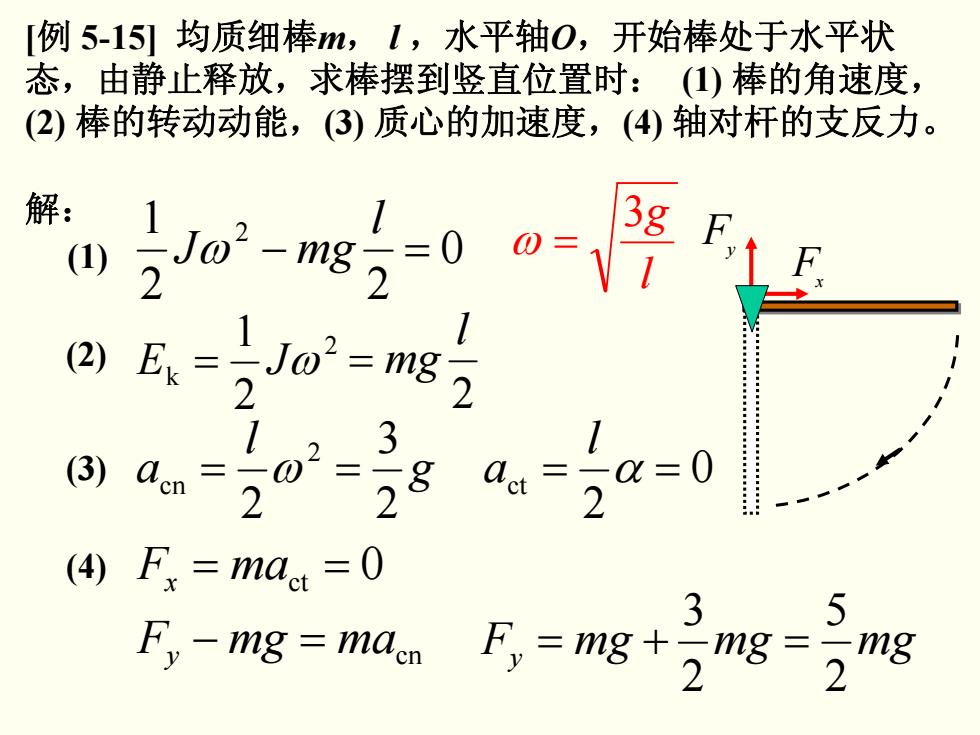
[例 5-15] 均质细棒m, l ,水平轴O,开始棒处于水平状 态,由静止释放,求棒摆到竖直位置时: (1) 棒的角速度, (2) 棒的转动动能,(3) 质心的加速度,(4) 轴对杆的支反力。 解: 0 2 2 1 2 =− l ω mgJ l 3g ω = (2) 2 k 21 = JE ω (3) 2 3 2 2 cn g l a ω == F x F y 0 x = maF ct = y mamgF cn (4) − = y mgmgmgF 25 23 =+= (1) 2 l = mg 0 2 ct α == l a

[例5-16]细杆A:(m,)可绕轴转动,水平处静止释 放,在竖直位置与静止物块B:(m发生弹性碰撞,求 碰后:(1)物块B的速度yg,(2)细杆A的角速度@2,(3) 细杆A转过的最大角度 maxo 解:mgL=Jo A 2 2 1 J=mL 3g 2.0=1 B 3 J01 J02 2 VB- 3gL.@:= 3g 碰后反方向转动
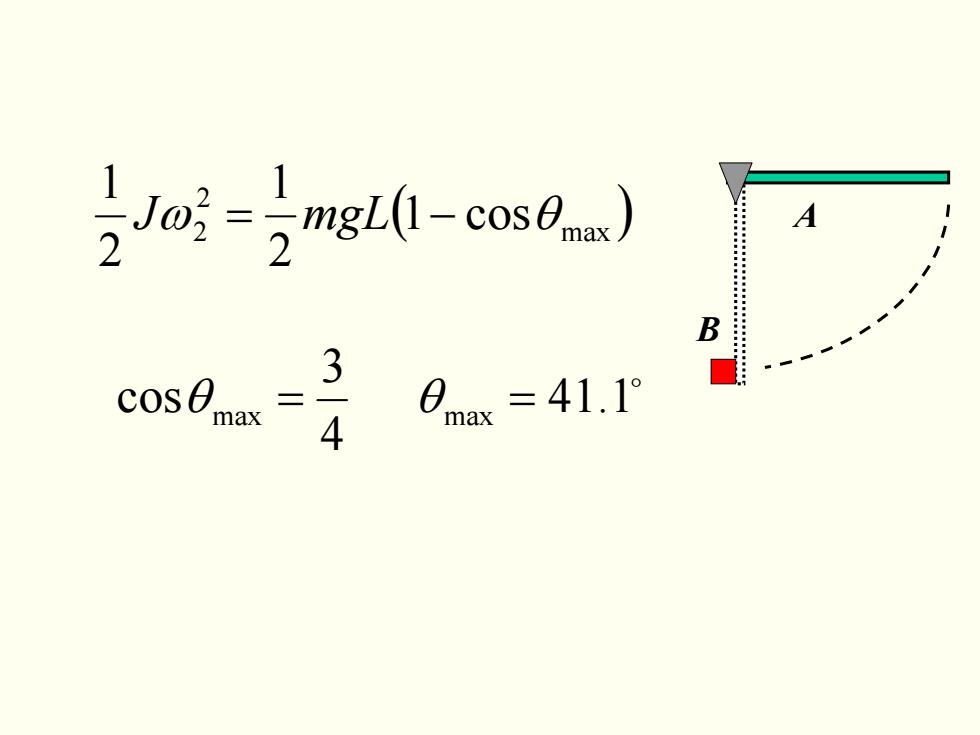
2 1 2 1 2 1 = JmgL ω L g mLJ 3 3 1 1 2 ω =∴= 解: ⎪⎩ ⎪ ⎨ ⎧ += += 2 2 2 2 1 21 2 1 2 1 2 1 B B mvJJ LmvJJ ωω ωω L g gLvB 3 2 1 3 2 1 = ω2 −= 碰后反方向转动。 B A [ 例5-16] 细杆A : (m , L )可绕轴转动,水平处静止释 放,在竖直位置与静止物块B : ( m ) 发生弹性碰撞,求 碰后: (1)物块 B的速度 v B ,(2)细杆A 的角速度 ω2 , (3) 细杆A转过的最大角度 θ max
B 4 8nmax=41.1
( ) max 22 cos1 21 21 Jω mgL −= θ o 1.41 4 3 cosθ max = θ max = B A