
第7章狭义相对论基础 §7.1经典力学的因难 §7.2狭义相对论的基本假设 §7.3洛伦兹变换 §74狭义相对论的时空观 §7.5相对论力学 §7.6狭义相对论的进一步讨论
第 7 章 狭义相对论基础 §7.1 经典力学的困难 经典力学的困难 §7.2 狭义相对论的基本假设 §7.5 相对论力学 §7.4 狭义相对论的时空观 狭义相对论的时空观 §7.3 洛伦兹变换 §7.6 狭义相对论的进一步讨论
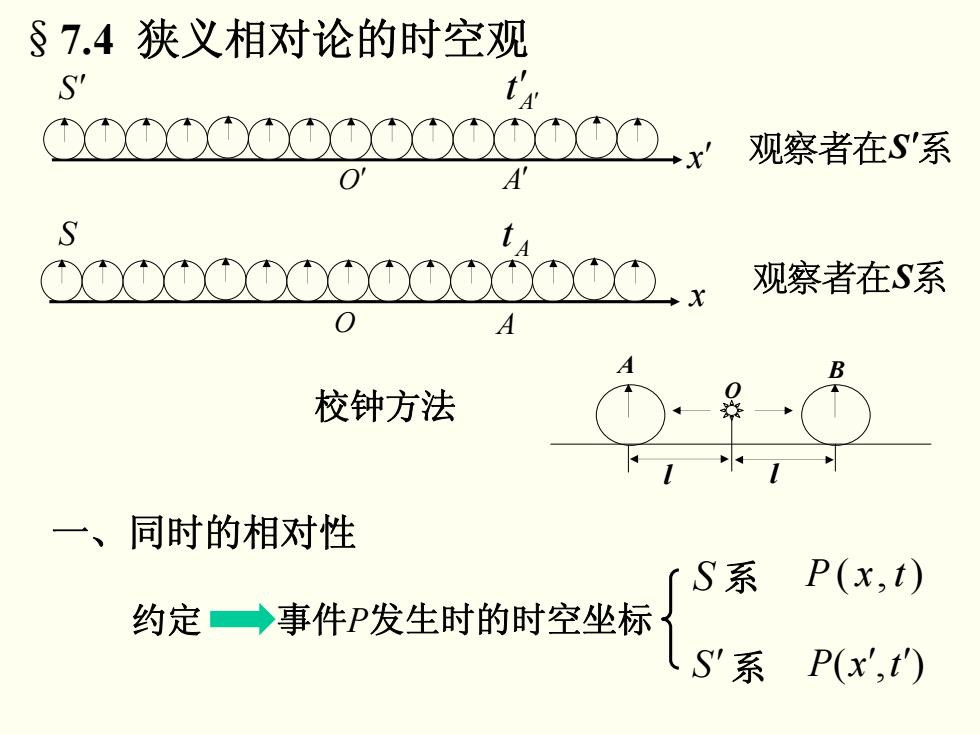
§7.4狭义相对论的时空观 t XOOXX①XXX0x 观察者在S系 A Bccxxooxdoo 观察者在S系 校钟方法 一、同时的相对性 〔S系P(x,t) 约定→事件P发生时的时空坐标 S'系P(x',t)
x O A S At x ′ O′ A′ S′ At ′ ′ 一、同时的相对性 约定 事件P发生时的时空坐标 S 系 S′系 P ( x, t) P(x′,t′) 校钟方法 §7.4 狭义相对论的时空观 O A B l l 观察者在S系 观察者在S′系

S系 事件1 (x1,t1) 事件2(x2,t2) 两事件同时发生 t1=t2 S'系 事件1(x1,) 事件2(x2,t2) 6-=? u = c2, t1- t2- 2= 111 、 /、 u2
事件 1 ),( 事件 2 11 tx ),( 22 tx 两事件同时发生 21 = tt S 系 ),( 11′ tx ′ ),( 22′ tx ′ ? ′ −tt 12 ′ = S′系 事件 1 事件 2 2 2 1 2 1 1 1 c u x c u t t − − ′ = 2 2 2 2 2 2 1 c u x c u t t − − ′ = 2 2 2 21 12 1 )( c u xx c u tt − − ′ − ′ =

S系 同地发生的两个同时事件 X1=X2 t好=t2 S系 异地发生的两个同时事件 X1>X2 t3> X1<X2 →t5< t1- c2 X1 t2 -X2 t= -C .2 u2 (x1-x2) t' 。2
2 2 1 2 1 1 1 c u x c u t t − − ′ = 2 2 2 2 2 2 1 c u x c u t t − − ′ = 2 2 2 21 12 1 )( c u xx c u tt − − ′ − ′ = S 系 同地发生的两个同时事件 21 = xx 21′ = tt ′ S 系 异地发生的两个同时事件 21 > xx 12′ > tt ′ 21 < xx 12′ < tt ′

S系 同地发生的两个同时事件 X1=X2 t1=t? S系 异地发生的两个同时事件 X1>X2 3>t1 X1<X2 b<t S系上的观察者认为自己所有的时钟都已校准了的时 侯,S”系上的各时钟是否也都校准了呢? S'系上的观察者认为自己所有的时钟都已校准了的时 侯,S系上的各时钟是否也都校准了呢?
S 系上的观察者认为自己所有的时钟都已校准了的时 侯,S′系上 的各时钟是否也 都校准了呢? S 系 上的观察者认为自己所有的时钟都已校准了的时 侯, S′系 上的各时钟是否也 都校准了呢? S 系 同地发生的两个同时事件 21 = xx 21′ = tt ′ S 系 异地发生的两个同时事件 21 > xx 12′ > tt ′ 21 < xx 12′ < tt ′
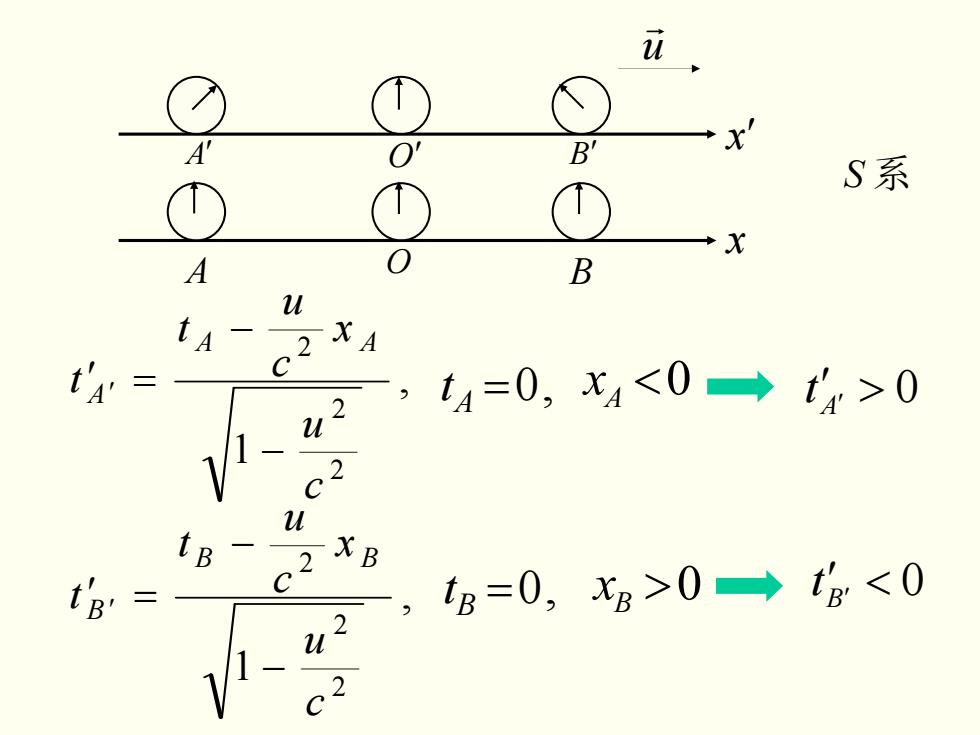
O' B 比 S系 X B u 、XA 2,=0,x0 1 2 u c ,tB=0,xg>0→tg<0 u
A O B A′ O′ B′ x x ′ u r , 1 2 2 2 c u x c u t t A A A − − ′ ′ = , 1 2 2 2 c u x c u t t B B B − − ′ ′ = ′ ′ > 0 A =0, t At 0 Bx S 系
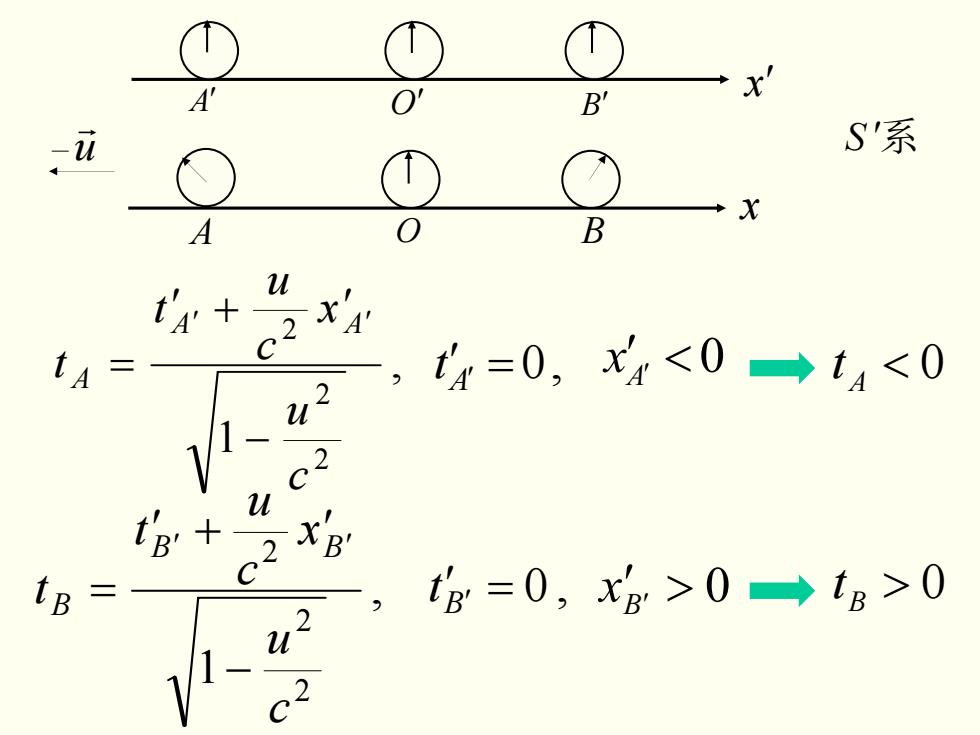
A 0' B 比 -u S系 A 0 B -x t+ u XA tr=0,x40→tg>0
, 1 2 2 2 c u x c u t t A A A − ′ + ′ = ′ ′ , 1 2 2 2 c u x c u t t B B B − ′ + ′ = ′ ′ 0 > 0 B ′ t x B′ A O B A′ O′ B′ x x′ u r S ′系

二、运动时钟的变慢 S系 P(xi,t) P(x2,2) xf =x, S系P(x,t) P2(x2,t2) t2-t1= 红总 u 2>1 →t2-t>t)-t
二、运动时钟的变慢 S ′系 ),( 111 ′ txP ′ ),( 222 ′ txP ′ S 系 ),( 111 txP ),( 222 txP ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ′ − ′ + ′ − ′ − =− )()( 1 1 12 2 12 2 2 12 xx c u tt c u tt 21′ = xx ′ 1 1 1 2 2 > − c u 1212 − > ′ − tttt ′ 2 2 12 1 c u tt − ′ − ′ =

某物体内部相继发生的两个事件P S系 P(xt) P2(xp:t2) △t'=t)-t S系 P(x1,41) P2(x2,t2) △t=t2-t1 △t △t= u 随某物体 (S系)一起运动的时钟所指示的时间 △T △t= 该物体的固有时△( △T=△t' △t>△t 运动物体上发生的自然过程比起静止物体的同样 过程延缓了 ◆运动时钟的延缓
某物体内部相继发生的两个事件 P1 P2 S ′系 ),( 11 ′ p txP ′ ),( 2 2 ′ p txP ′ 12 Δ ′ = ′ − ttt ′ S 系 ),( 111 txP ),( 222 txP 12 Δ = − ttt 2 2 1 c u t t − Δ ′ =Δ 随某物体 一起运动的时钟所指示的时间 ( ) S ′系 该物体的固有时 Δ τ 2 Δ τ = Δ t′ 2 1 c u t − Δ =Δ τ Δ t Δ> τ 运动物体上发生的自然过程比起静止物体的同样 过程延缓了 运动时钟的延缓
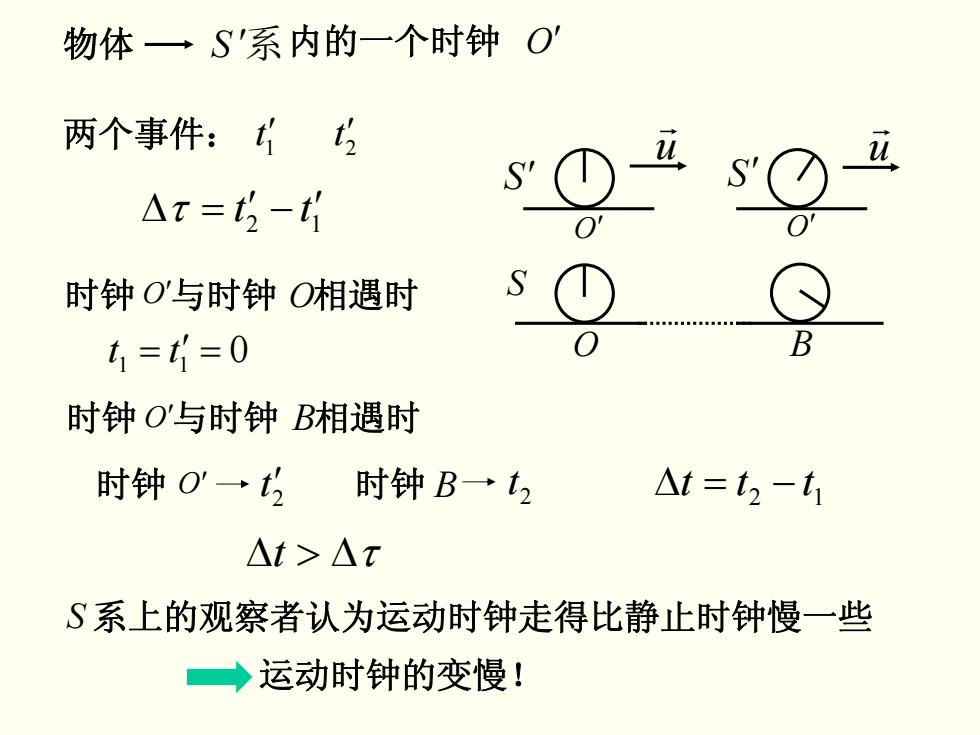
物体一S'系内的一个时钟 O 两个事件:t △t=t3-t好 时钟O'与时钟O相遇时 t1=t=0 时钟O'与时钟B相遇时 时钟O'一·t2 时钟B→t2 △t=t2-t1 △t>△t S系上的观察者认为运动时钟走得比静止时钟慢一些 ◆运动时钟的变慢!
两个事件: 21′ tt ′ 12 Δτ = ′ − tt ′ S′ S u r O′ O′ O S′ u r B 时钟 与时钟 相遇时 O′ O 0 = tt 11 ′ = 时钟 与时钟 相遇时 O′ B 时钟 O′ 2t′ 时钟 2 B t 12 Δ = − ttt t >Δ Δτ 运动时钟的变慢! S 系上的观察者认为运动时钟走得比静止时钟慢一些 物体 S ′系内的一个时钟 O′