
第门章狭义相对论基础
第 7 章 狭义相对论基础

第7章狭义相对论基础 §7.1经典力学的因难 §7.2狭义相对论的基本假设 §7.3洛伦兹变换 §7.4狭义相对论的时空观 §7.5相对论力学 §7.6狭义相对论的进一步讨论
第 7 章 狭义相对论基础 §7.1 经典力学的困难 经典力学的困难 §7.2 狭义相对论的基本假设 §7.5 相对论力学 §7.4 狭义相对论的时空观 狭义相对论的时空观 §7.3 洛伦兹变换 §7.6 狭义相对论的进一步讨论

§7.1经典力学的困难 一、力学相对性原理和伽利略变换 惯性系S 在两个惯性系中考察同一物理事件 惯性系S 在S系中空间各点放置无穷系列的时钟,这些时 钟与该惯性系保持相对静止、彼此同步。一个事件的 时空坐标(x,y,z,t)由该事件发生的地点及该处的时钟 记录下来。 伽利略变换: 惯性系S 惯性系S S'系相对于S系运动 t时刻,物体到达P点 事件P
在两个惯性系中考察同一物理事件 t 时刻,物体到达P 点 一、力学相对性原理和伽利略变换 事件 P 惯性系 惯性系 S S′ S ′ 系相对于 S 系运动 伽利略变换: §7.1 经典力学的困难 在 系中空间各点放置无穷系列的时钟,这些时 钟与该惯性系保持相对静止、彼此同步。一个事件的 时空坐标 由该事件发生的地点及该处的时钟 记录下来。 tzyx ),,,( S 惯性系 S 惯性系 S′
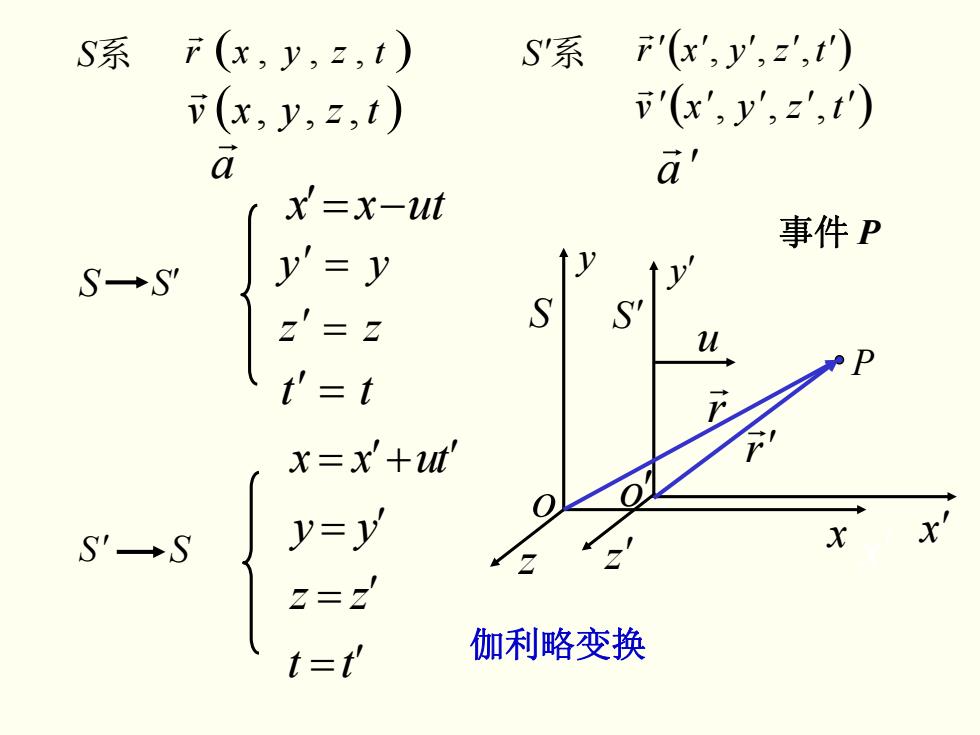
S系 F(x,y,=,1) S系 '(x',y,z,t) (x,y,,t) '(x,y,z',t) a a' X=x-ut 事件P S一S y'=y z′=z S t'=t x=x'+ut 公 y=y 2=z t=t 伽利略变换
′ = −utxx ′ = yy z ′ = z ′ = tt tt zz yy tuxx = ′ = ′ = ′ = ′+ ′ 事件 P S S′ S′ S P r r o ′ S′ u x ′ x o S y r ′ r y ′ z z ′ x ′ 伽利略变换 ′( ′ ′ ′,,, tzyxr ′) r S′系 ′( ′ ′ ′,,, tzyxv ′) r a ′ r ( ) ,,, tzyxrr S系 ( ) ,,, tzyxvr a r
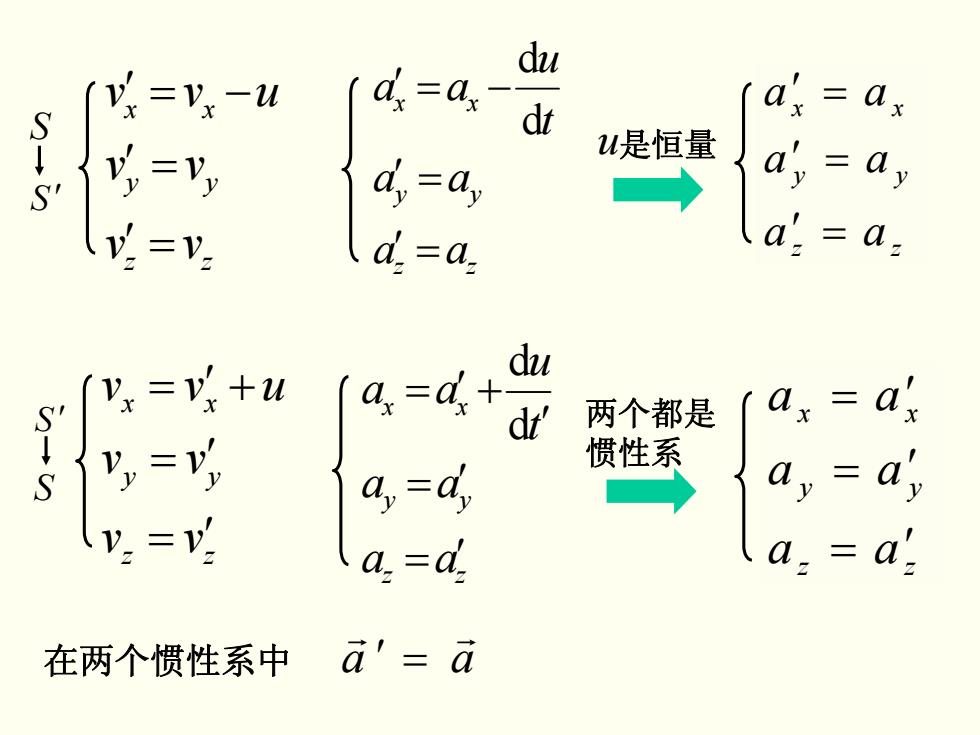
du V=Vx-u a.=ax dt :x S ↓ u是恒量 =Y d,=ay v.=V. d.=a. d (Yx=v+u du a.=d4+ dr' 两个都是 ax=a ↓ 惯性系 a,=d, v.=v. a=d a a 在两个惯性系中 a'=a
两个都是 惯性系 u是恒量 在两个惯性系中 aar r ′ = zz yy xx vv vv uvv ′ = ′ = ′ = − zz yy xx vv vv uvv = ′ = ′ = ′ + zz yy xx aa aa t u aa ′ = ′ = ′ −= d d zz yy xx aa aa t u aa = ′ = ′ ′ = ′ + d d zz yy xx aa aa aa = ′ = ′ = ′ zz yy xx aa aa aa ′ = ′ = ′ = S S ′ S S ′

二、牛顿的相对性原理 S系 m a m a S系F m' a' m'a' 在牛顿力学中 力与参考系无关 质量与运动无关 宏观低速物体的力学规律在任何惯性系中形式相同。 或:力学的基本运动规律在所有惯性系中可以表示 为相同形式。 或:所有惯性系都是等价的
二、牛顿的相对性原理 在牛顿力学中 力与参考系无关 质量与运动无关 ′ = amF ′′ r r F r m a r amF r r S 系 = F ′ r m ′ a ′ r S′系 宏观低速物体的力学规律在任何惯性系中形式相同。 或:力学的基本运动规律在所有惯性系中可以表示 为相同形式。 或:所有惯性系都是等价的

如:动量守恒定律 S系 m11+m2下2=m110+m2下20 S系 m+m22=m10+m220 伽利略变换的困难 电磁场方程组不服从伽利略变换 特定的惯性参考系 ● ● •绝对惯性系 以太
S 系 1012211 202 vmvmvmvm r r r r + = + S ′系 1012211 202 ′ ′ + ′ ′ = ′ ′ + ′ vmvmvmvm ′ r r r r 如:动量守恒定律 伽利略变换的困难 电磁场方程组不服从伽利略变换 •特定的惯性参考系 •以太 •绝对惯性系 S′ u ′ S′′ S u′′ ⋅⋅⋅
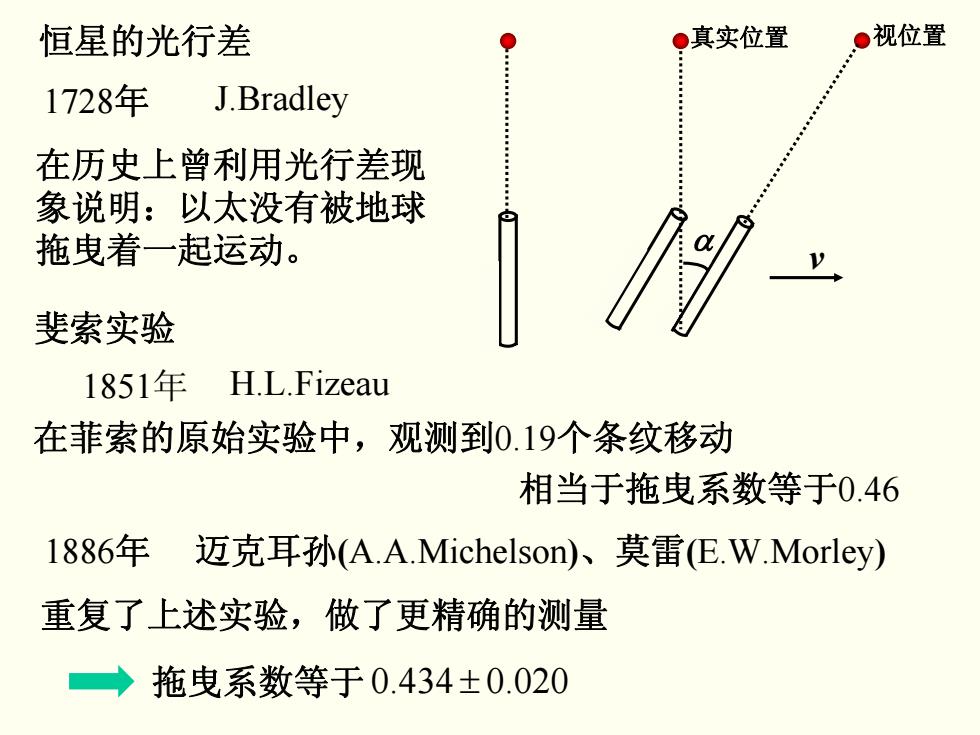
恒星的光行差 ●真实位置 ●视位置 1728年 J.Bradley 在历史上曾利用光行差现 象说明:以太没有被地球 拖曳着一起运动。 斐索实验 1851年 H.L.Fizeau 在菲索的原始实验中,观测到0.19个条纹移动 相当于拖曳系数等于0.46 1886年 迈克耳孙(A.A.Michelson)、莫雷(E.W.Morley) 重复了上述实验,做了更精确的测量 →拖曳系数等于0.434±0.020
v α 恒星的光行差 真实位置 视位置 1728年 J.Bradley 斐索实验 1851年 H.L.Fizeau 在历史上曾利用光行差现 象说明:以太没有被地球 拖曳着一起运动。 在菲索的原始实验中,观测到0.19个条纹移动 1886年 迈克耳孙(A.A.Michelson)、莫雷(E.W.Morley) 相当于拖曳系数等于0.46 拖曳系数等于 0.434 ± 0.020 重复了上述实验,做了更精确的测量

早在19世纪初,菲涅耳(A.J.Fresnel)就考虑过运动物质对 以太的拖曳作用,推导出:在运动着的物质中,当光传播方 向和物质运动方向相同或相反时,光速分别为 u=C±v1- (同向取正号,反向取负号) 其中1-正是拖曳系数 n水=1.333 ◆ =0.438 →历史上菲索实验的结果证实了上式 19世纪中叶,菲索实验曾被理解为以太存在和以太被运动物 质部分拖曳的“证据” 在大气中进行光学实验时 大气的折射率非常接近于1 大气的拖曳系数1- →0 可认为没有拖曳作用。 n 在大气中进行光学实验时,可把以太看作绝对静止的参考系 →测量地球的绝对运动仍有可能
) 1 1( 2 n v n c u −±= 早在 19世纪初,菲涅耳 (A. J. Fresnel) 就考虑过运动物质对 以太的拖曳作用,推导出:在运动着的物质中,当光传播方 向和物质运动方向相同或相反时,光速分别为 (同向取正号,反向取负号) 438.0 1 1 2 =− n水 其中 21 1 n − 正是拖曳系数 n水 = 333.1 历史上菲索实验的结果证实了上式 19世纪中叶,菲索实验曾被理解为以太存在和以太被运动物 质部分拖曳的“证据” 在大气中进行光学实验时 大气的折射率非常接近于 1 大气的拖曳系数 0 1 1− 2 → n 在大气中进行光学实验时,可把以太看作绝对静止的参考系 可认为没有拖曳作用 测量地球的绝对运动仍有可能