
第8章热力学平衡态
第 8 章 热力学平衡态

热物理学 组成物质的分子或粒子都在作永不停息的无规则 运动,称为热运动。大量分子热运动的集体效应在宏 观上表现为物体的热现象和热性质。 研究分子热运动,讨论热现象的规律、分析物体 热性质的理论称为热物理学。 热物理学包括宏观理论和微观理论。 ·宏观理论— 热力学:以观察和实验为基础,通过归 纳和推理得出有关热现象的基本规律,因而其结论普 遍而且可靠。 ·微观理论一分子动理论:从分子结构和分子运动出 发,应用力学规律和统计方法,研究大量分子热运动 的集体效应,从微观本质上解释热现象和热性质
热物理学 组成物质的分子或粒子都在作永不停息的无规则 运动,称为热运动。大量分子热运动的集体效应在宏 观上表现为物体的热现象和热性质。 研究分子热运动,讨论热现象的规律、分析物体 热性质的理论称为热物理学。 热物理学包括宏观理论和微观理论。 • 宏观理论——热力学:以观察和实验为基础,通过归 纳和推理得出有关热现象的基本规律,因而其结论普 遍而且可靠。 • 微观理论——分子动理论:从分子结构和分子运动出 发,应用力学规律和统计方法,研究大量分子热运动 的集体效应,从微观本质上解释热现象和热性质

第8章热力学平斯态 §8.1热力学系统平衡态 §8.2热力学第零定律 温度和温标 §8.3理想气体温标和状态方程 §8.4理想气体微观模型压强和温度的 统计意义 §8.5能量均分定理 §8.6麦克斯韦速率和速度分布 §8.7玻尔兹曼分布 §8.8量子统计分布简介
§8.1 热力学系统 平衡态 第 8 章 热力学平衡态 §8.2 热力学第零定律 温度和温标 §8.3 理想气体温标和状态方程 §8.4 理想气体微观模型 压强和温度的 统计意义 §8.5 能量均分定理 §8.6 麦克斯韦速率和速度分布 §8.7 玻尔兹曼分布 §8.8 量子统计分布简介

§8.1热力学系统平衡态 一、热力学系统 热力学系统:所研究的宏观物体或物体组。 孤立系统:与外界无能量、质量交换的系统。 二、系统状态的描述 宏观参量:可以直接测量的量,如压强、温度。 由宏观参量描述的系统状态称为宏观状态。 微观参量:一般无法直接测量,如分子的位置、 速度。 由微观参量描述的系统状态称为微观状态
一、热力学系统 §8.1 热力学系统 平衡态 热力学系统:所研究的宏观物体或物体组。 孤立系统:与外界无能量、质量交换的系统。 二、系统状态的描述 宏观参量:可以直接测量的量,如压强、温度。 由宏观参量描述的系统状态称为宏观状态。 微观参量:一般无法直接测量,如分子的位置、 速度。 由微观参量描述的系统状态称为微观状态
三、平衡态 热力学平衡态:孤立系统经过一段时间,其宏 观性质不再发生变化,其内部不存在宏观的质 量、能量流动。 例 P1>P2 初态 末态 讨论 (1)与稳定态不同 100°C 0°C (2)热动平衡 (3)理想状态
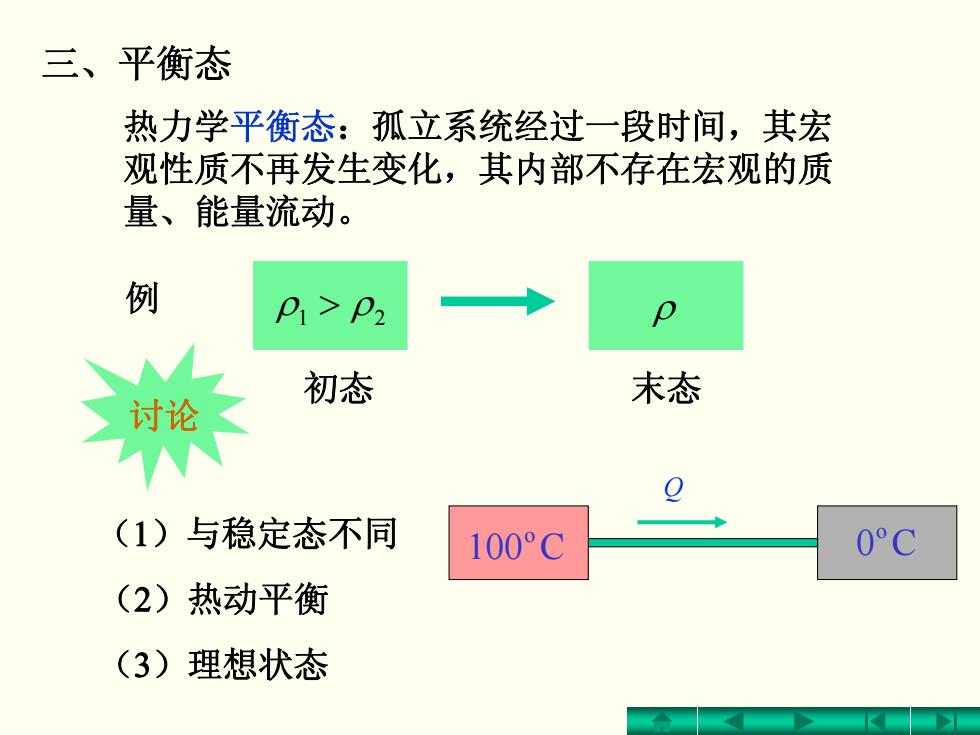
三、平衡态 热力学平衡态:孤立系统经过一段时间,其宏 观性质不再发生变化,其内部不存在宏观的质 量、能量流动。 (1)与稳定态不同 (2)热动平衡 (3)理想状态 讨论 例 ρ > ρ 21 初态 ρ 末态 Q C100o C0o

四、状态参量 当系统处于平衡态,其宏观属性可用一组独立 的宏观量来描述— 状态参量 状态参量可分为两类: (1)广延量:整个系统的参量值等于系统中各 部分相应参量值的和。 F=∑E 例:摩尔数 (2)强度量:此类参量可以在系统内逐点测量。 F=F 例:温度 END
四、状态参量 当系统处于平衡态,其宏观属性可用一组独立 的宏观量来描述——状态参量 (1)广延量:整个系统的参量值等于系统中各 部分相应参量值的和。 = ∑ i FF i (2)强度量:此类参量可以在系统内逐点测量。 = FF i 例:摩尔数 例:温度 状态参量可分为两类: END