
第5章利体力学基础 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动
§5.2刚体的定轴转动定理 刚体是一个特殊的质点系,描述质点系转动的动 力学方程: dL 一、刚体所受的力矩 dt 取惯性坐标系O'xz,z轴为固定转轴 X 说明1.对于质点系,由于所有内力对任意参考点的力矩为 零,则刚体所受相对于原点O的力矩等于合外力矩。 2.由于外力矩在垂直于转轴方向上的分量M被轴承上 支承力的力矩所抵消,只需要考虑由外力在垂直于转轴 方向的分量产生的沿转轴方向的力矩M
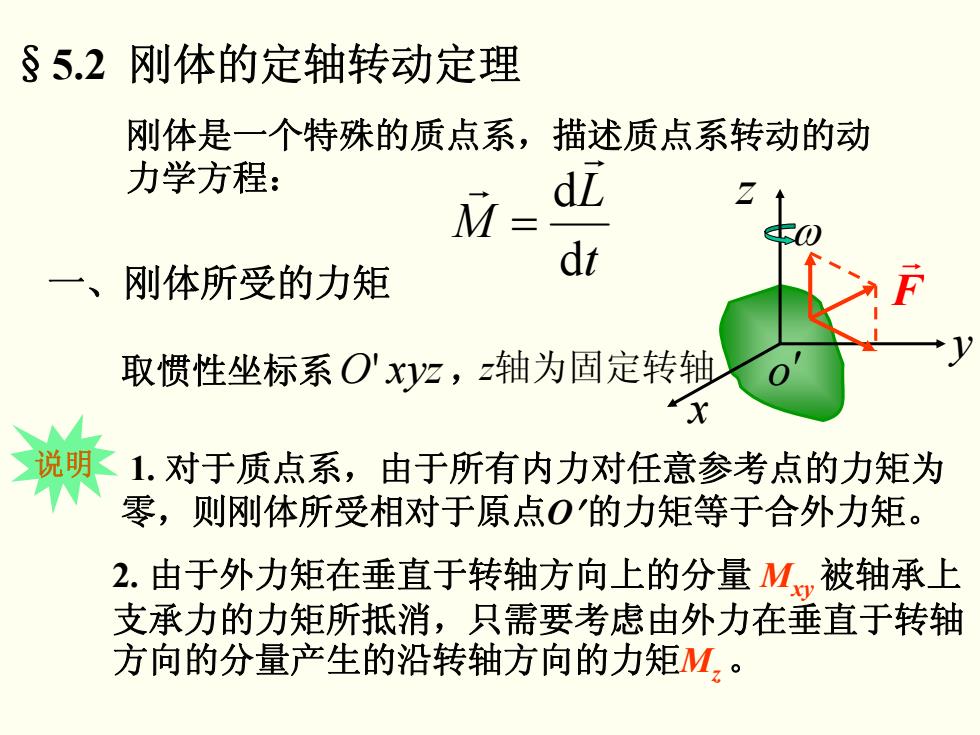
刚体是一个特殊的质点系,描述质点系转动的动 力学方程: t L M d d r r = 1. 对于质点系,由于所有内力对任意参考点的力矩为 零,则刚体所受相对于原点 O ′的力矩等于合外力矩。 一、刚体所受的力矩 2. 由于外力矩在垂直于转轴方向上的分量 Mxy被轴承上 支承力的力矩所抵消,只需要考虑由外力在垂直于转轴 方向的分量产生的沿转轴方向的力矩 Mz 。 §5.2 刚体的定轴转动定理 说明 o′ x y z ω F r 取惯性坐标系 , ' xyzO z轴为固定转轴
设第i个质元受外力至,并假定 F垂直于转轴。 所受相对于0点的外力矩为: M,=R×F:R=o0+ M,=o+动小x方 =o'0×F+E×F 也被抵消 Lz轴 ∥z轴 R Me=厅×F=rE,sine, 刚体所受的相对于轴的合力矩: M.=∑M=∑rE,sn8
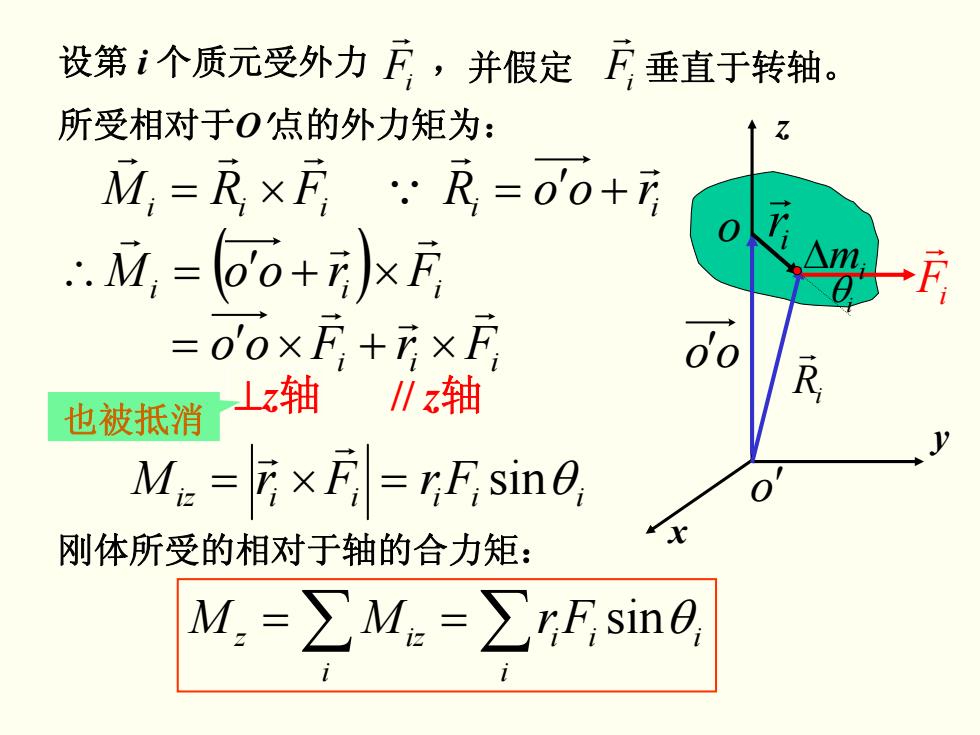
r 设第 Fi i 个质元受外力 ,rFi 并假定 垂直于转轴。 FRM iii r r r ×= // z轴 i irooR r r Q = ′ + x y z o o ′ r Ri r Fi ir r Δmi θi ′ oo ( ) i FrooM ii r r r =∴ ′ ×+ FrFoo iii r r r = ′ ×+× ⊥z轴 也被抵消 FrFrM θ iiiiiiz =×= sin r r 所受相对于O′点的外力矩为: 刚体所受的相对于轴的合力矩: ∑ == ∑ i iii i z iz FrMM sinθ
二、刚体定轴转动的角动量 刚体所受的相对于0'的角动量: i=∑i,=∑(R×△m,) ,1E,R,,)元,1 i L R 共面 L=R·△m,y y Le=L,sinp,=R·△m,y,sinp,=y△m,y
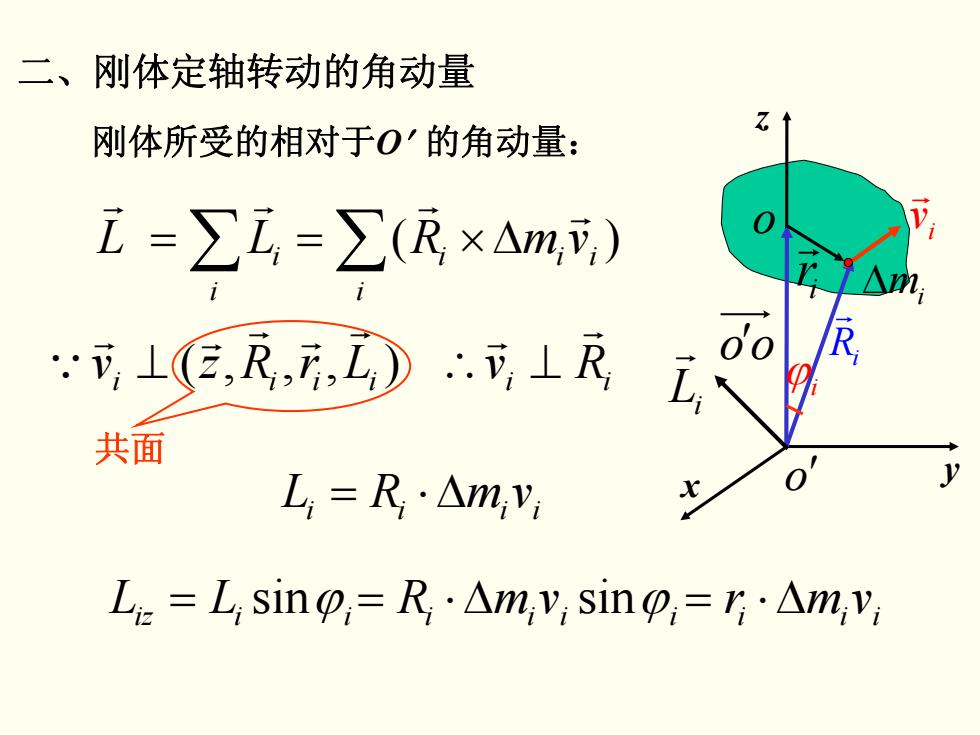
刚体所受的相对于O′ 的角动量: ∑ ∑ Δ×== )( i iii i i vmRLL r r r r i iii RvLrRzv ii r r r r r r r Q ⊥ ),,,( ⊥∴ iiii = ⋅Δ vmRL 共面 LL ϕiiiz = sin 二、刚体定轴转动的角动量 x z o o ′ Ri r ir r Δmi ′ oo i v r Li r y ϕi iiii = ⋅Δ vmR sinϕ iii = ⋅Δ vmr

对整个刚体: L=∑L.=∑Amy=(∑Amo J三∑△m,称为刚体对转轴z的转动慢量。 L=Jo 为刚体相对于转轴z的角动量
对整个刚体: =∑ i z LL iz z = JL ω 称为刚体对转轴 z 的转动惯量。 2i i i ∑Δ≡ rmJ 为刚体相对于转轴 z 的角动量。 ∑ ∑Δ=Δ= i ii i iii rmvmr )( ω2

三、刚体定轴转动定律 由质点系的角动量定理: M dL 对刚体的定轴转动,有:M dL dt dJo) 而且L.=J0 M-M. 得到:M= dt 设转动过程中不变,则有: M=J do dt 刚体定轴转动定律:刚体在作定轴转动时,刚体的角 加速度与它所受到的合外力矩成正比,与刚体的转动惯 量成反比
t L M z z dd = 得到: ( ) t J M d d ω = α ω J t JM = d d = 刚体定轴转动定律: 设转动过程中J不变, 则有: 由质点系的角动量定理: t L M d d r r = 对刚体的定轴转动,有: z = ω = MMJL z 而且 三、刚体定轴转动定律 刚体在作定轴转动时,刚体的角 加速度与它所受到的合外力矩成正比,与刚体的转动惯 量成反比

do M=J Ja dt >是关于刚体定轴转动的动力学方程。(与F=ma比较) 推广到J可变情形: Mdt=d(Jo 刚体定轴转动的角动量定理 Mdt-[d(J@)-J-Jw0 Mdt 称为在,到t时间内作用在刚体上 的角冲量
推广到 J 可变情形: = dd (JtM ω) ( ) 00 0 00 dd ωωω ω ω JJJtM J J t t = −= ∫∫ ∫tt tM0 d 称为在 t0 到 t 时间内作用在刚体上 的角冲量。 ——刚体定轴转动的角动量定理 ¾ 是关于刚体定轴转动的动力学方程。 (与 F = ma 比较) α ω J t JM = d d =
[例5-1定滑轮:m,r,J,物体:m1,m2, 轻绳不能伸 长,无相对滑动。求滑轮转动的角加速度和绳的张力。 解:由于考虑滑轮的质量,T≠T, 问题中包括平动和转动。 mg-T ma T,-m2g ma Tr-Tr=Ja m,g 轮不打滑: a=ra 联立方程,可解得T1,T2,,。 m18 >此装置称阿特伍德机一可用于测量重力加速度g
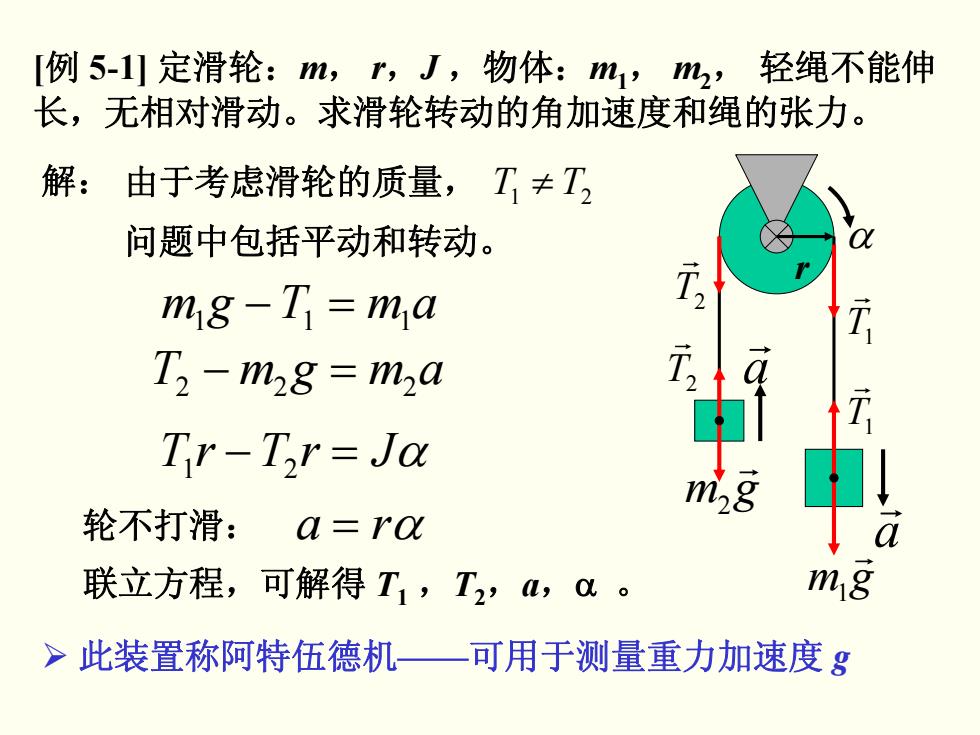
[例 5-1] 定滑轮:m, r,J ,物体:m1, m2, 轻绳不能伸 长,无相对滑动。求滑轮转动的角加速度和绳的张力。 − = 111 amTgm − 22 = 2amgmT − 21 = JrTrT α 解: 由于考虑滑轮的质量, ≠ TT 21 问题中包括平动和转动。 轮不打滑: = ra α 联立方程,可解得 T1 ,T2,a,α 。 ¾ 此装置称阿特伍德机——可用于测量重力加速度 g gm r 1 gm r 2 T1 r T1 r T2 r T2 r r a r a α r

「例5-21 均质细棒:m,1,对水平轴0:J=}ml2,铅 直位置时,一水平力F作用于距O为'处,计算0轴对棒 的作用力(称轴反力)。 解:设轴反力为Nx,N。 由转动定律:F'=JJC 由质心运动定律:F+V,=ma.mC“2 N-mg mdcy=ma=0 mg =贸-小= 讨论:当1'=(23)时,N=0,此时F的作用点称打击中心。 l'>(23)l时,N>0,I'<(23)时,N<0
[ 例5-2] 均质细棒: m , l ,对水平轴 O: ,铅 直位置时,一水平力 F 作用于距 O 为 l ′ 处,计算 O 轴对棒 的作用力(称轴反力)。 2 3 = 1 mlJ F r l ' ′ = JlF α O x maNF c x 解: + = y − = mamgN cy 得: ,1 2 3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ′ = l l x FN y = mgN 设轴反力为 Nx , Ny 。 由转动定律: 由质心运动定律: 当 l ′ =(2/3) l时, Nx =0 ,此时 F的作用点称打击中心 。 Ny l ′ > (2/3) l 时, Nx >0 , l ′ < (2/3) l时, Nx <0 。 r Nx r gm r c 讨论: 2 2 ω l = m 2 l = m α = 0
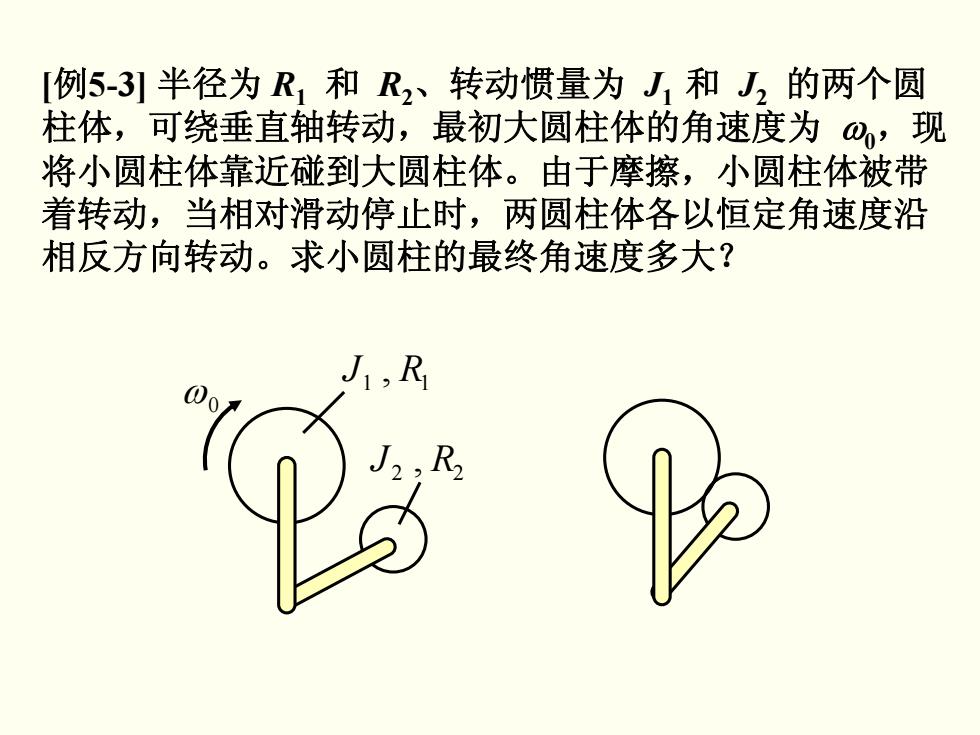
[例5-3]半径为R1和R2、转动惯量为J1和J2的两个圆 柱体,可绕垂直轴转动,最初大圆柱体的角速度为@,现 将小圆柱体靠近碰到大圆柱体。由于摩擦,小圆柱体被带 着转动,当相对滑动停止时,两圆柱体各以恒定角速度沿 相反方向转动。求小圆柱的最终角速度多大?
[例5-3] 半径为 R1 和 R2、转动惯量为 J1 和 J2 的两个圆 柱体,可绕垂直轴转动,最初大圆柱体的角速度为 ω0,现 将小圆柱体靠近碰到大圆柱体。由于摩擦,小圆柱体被带 着转动,当相对滑动停止时,两圆柱体各以恒定角速度沿 相反方向转动。求小圆柱的最终角速度多大? 11 , RJ 22 , RJ ω0