
第3章 机械能和功 §3.1功质点动能定理 §3.2保守力非保守力耗散力 §3.3质点在保守力场中的势能 §3.4质点系的势能 §3.5功能原理 能量守恒定律
第 3 章 机械能和功 §3.1 功 质点动能定理 §3.2 保守力 非保守力 耗散力 §3.3 质点在保守力场中的势能 §3.4 质点系的势能 §3.5 功能原理 能量守恒定律
§3.4质点系的势能 势能属于相互作用有保守力的各物体组成的整个 系统,称相互作用势能。与系统内的一对保守内力做 功有关。 一、质点系内力与外力 内力 系统内,内力是成对出现的。 外力
一、质点系 内力与外力 内力 外力 §3.4 质点系的势能 势能属于相互作用有保守力的各物体组成的整个 系统,称相互作用势能。与系统内的一对保守内力做 功有关。 系统内,内力是成对出现的

二、内力的功 一对内力的功: dr dA=F,·d+Fm·d Fy(d-d) =F,d(匠-) =-) 相对位矢 d,=d(-下)相对元位移 d dA=F·d
jjiiij rFrFA r r r r ⋅+⋅= ddd 二、内力的功 jiij rrr rr r = − ijij rFA r r ⋅= dd ij rrr ji )(dd 相对元位移 rr r = − j r r d j b r Fij r Fji ij rr irr d r ri j r r i b j a i a O i j 一对内力的功: r ri j ir r d j r r d ijij rr r r + d ij r r 相对位矢 d rrF jiij )(d r r r −⋅= )dd( jiij rrF r r r −⋅=
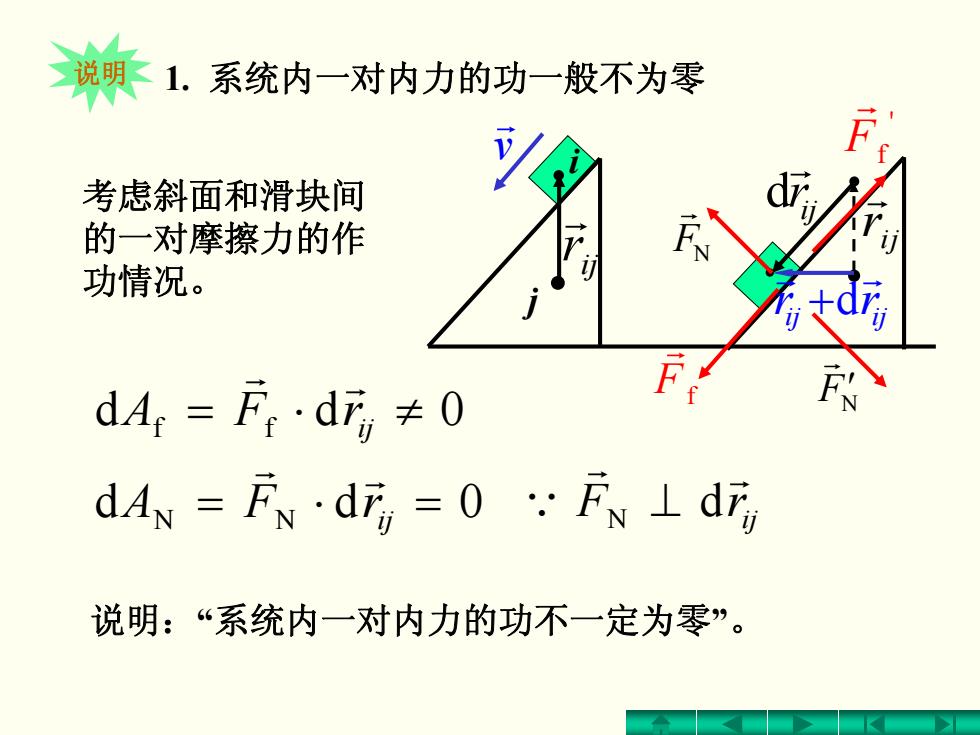
说明1.系统内一对内力的功一般不为零 考虑斜面和滑块间 的一对摩擦力的作 功情况。 dA=F·d7≠0 dA=F·df=0FN⊥d 说明:“系统内一对内力的功不一定为零
1. 系统内一对内力的功一般不为零 ff rFA ij ≠⋅= 0dd r r d 0d N N rFA ij =⋅= r r ij rF r r Q d N ⊥ 说明 ⋅ ⋅ ⋅ ⋅ i j r rij ij r rd ' Ff r Ff r FN r N F′ r v r ⋅ ij r r ijij rr r r +d 考虑斜面和滑块间 的一对摩擦力的作 功情况。 说明:“系统内一对内力的功不一定为零
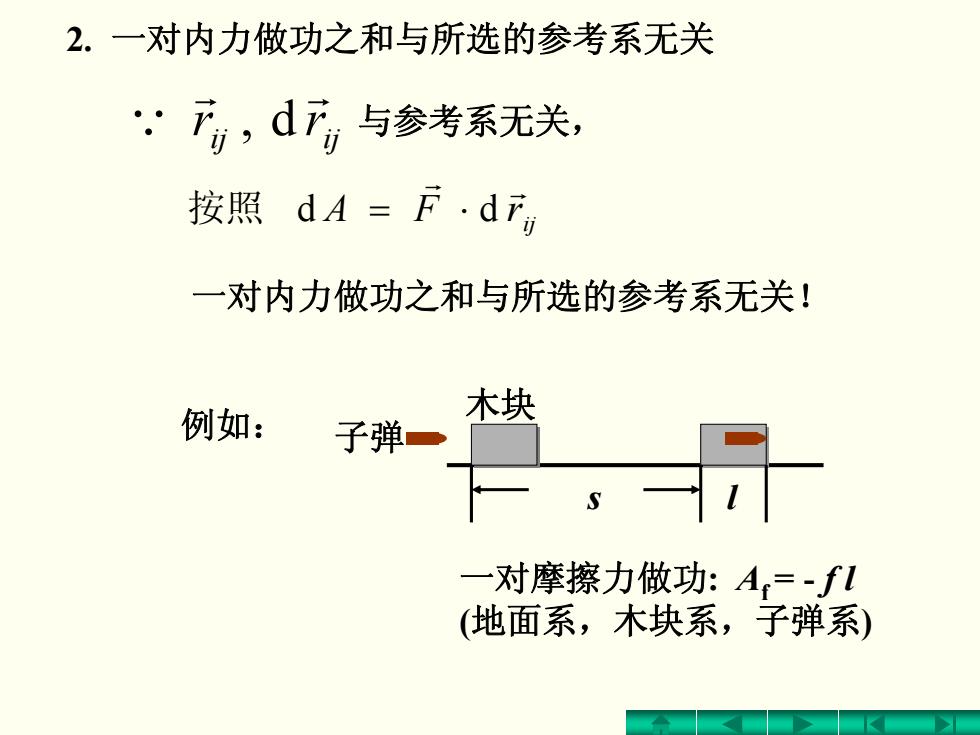
2.一对内力做功之和与所选的参考系无关 下前,d下与参考系无关, 按照dA=F·dF 一对内力做功之和与所选的参考系无关! 例如: 木块 子弹一 一对摩擦力做功:A=-f1 (地面系,木块系,子弹系)
2. 一对内力做功之和与所选的参考系无关 ijij rr r r Q d, 与参考系无关, 一对摩擦力做功: Af = - f l (地面系,木块系,子弹系) s l 子弹 木块 ij rFA r r 按照 d ⋅= d 一对内力做功之和与所选的参考系无关! 例如:

三、相互作用势能 一对内力作功: Au =dA=F,dr, d 一对保守内力→E,() Ab=-(E()-E,(a) A=心(fn·d+f·d) =心万-d 因此,在计算一对内力作功时,可选其中一个物体为参 考系,以另一物体的相对位移为准求内力做功。 如:重力势能E。=mgz属于地球和物体组成的系统
三、相互作用势能 ∫∫ ⋅== ba ijij ba ab rFAA r r d d )( p ij 一对保守内力 rE r ))()(( ab p b p arErEA r r = − − i j 因此,在计算一对内力作功时,可选其中一个物体为参 考系,以另一物体的相对位移为准求内力做功。 如: 重力势能 p = mgzE 属于地球和物体组成的系统。 )dd( jji b a ab iij rFrFA r r r r ⋅+⋅= ∫ 一对内力作功: br r r Fij r Fji r rij ir r d r ri jr rd j r r i b a j i a b j a r r O ∫ ⋅= ba ijji rF r r d

四、多质点系统的势能 E。=∑∑E ii>i) 保守内力 其中Ep剪为质点i和j之间的相互作用势能。 END
四、多质点系统的势能 ∑ ∑> = i i jj E E ij )( p p 保守内力 END 其中 为质点 E p ij i 和 j 之间的相互作用势能