
第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量
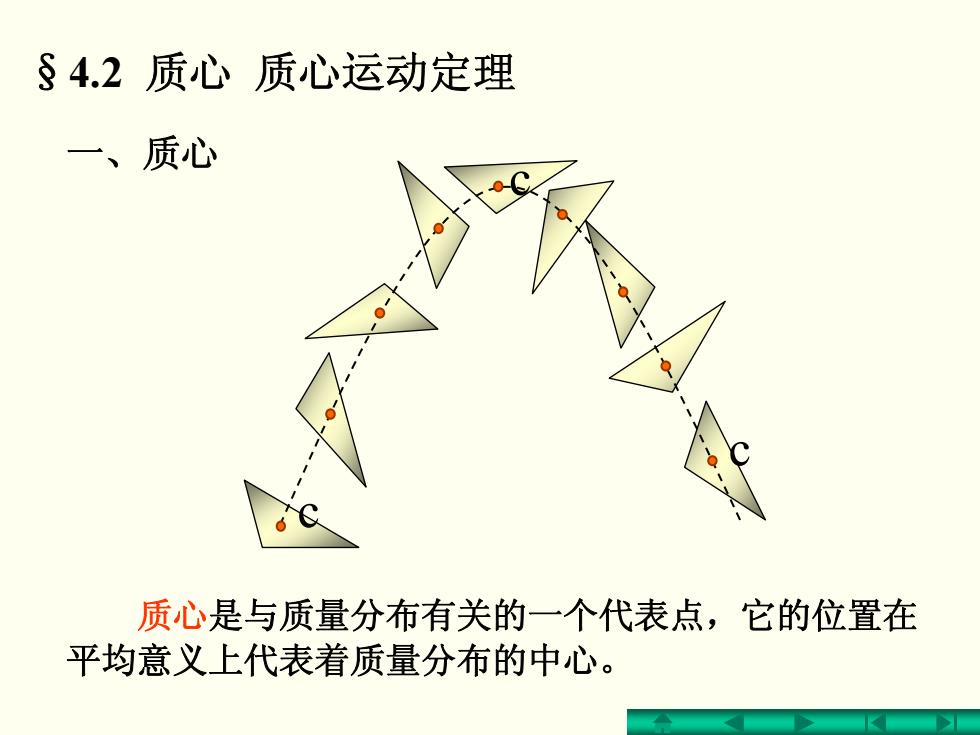
§4.2质心质心运动定理 一、质心 质心是与质量分布有关的一个代表点,它的位置在 平均意义上代表着质量分布的中心
§4.2 质心 质心运动定理 一、质心 质心是与质量分布有关的一个代表点,它的位置在 平均意义上代表着质量分布的中心。 c c c
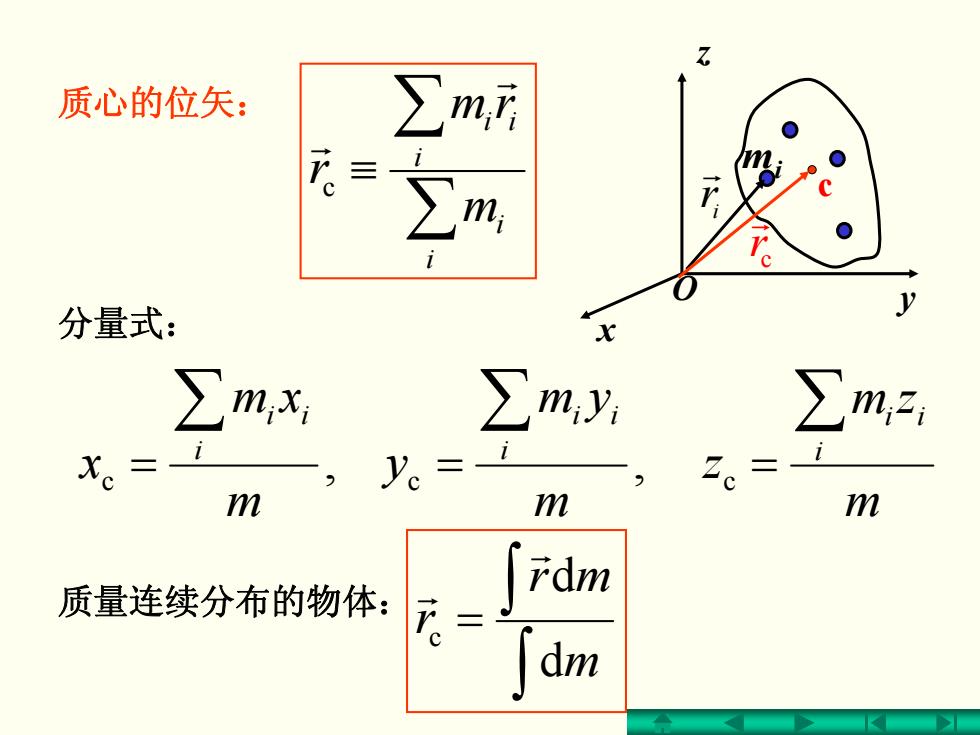
质心的位矢: ∑m,d 三 ∑ i 分量式: ∑m,x ∑m,y ∑m, 。= y。= 2。= m m m rdm 质量连续分布的物体: 元。= dm
质心的位矢: ∑ ∑ ≡ i i i ii m rm r r r c , c m xm x i ∑ ii = 分量式: ∫ ∫ = m mr r d d c r r , c m ym y i ∑ ii = m zm z i ∑ ii c = 质量连续分布的物体: x y z ir r mi cr r O c

rdm 分量式: 「dm ∫xdm ∫dm 质量线分布:dm=p,dl 质量面分布: dm=pds 质量体分布:dm=pdV
∫ ∫ = m mx x d d c 分量式: = ρ sdd sm = ρ dd Vm 质量线分布: 质量面分布: 质量体分布: ∫ ∫ = m mr r d d c r r ∫ ∫ = m my y d d c ∫ ∫ = m mz z d d c = ρ ldd lm

[例4-5求半圆环的质心。 解:dm=P,dl=P,Rd0 x。=∫xdn/m =jxp,Rd/元Rp, -@l0=2R 元 >质心不一定位于物体内部
[例4-5] 求半圆环的质心。 = ∫ l d πRRx ρθρ l mmxx ∫ = d c ∫ = π 0 dsin π 1 R θθ ¾ 质心不一定位于物体内部。 解: θ R x y O dl c π 2R = = ρ = ρll Rlm ddd θ
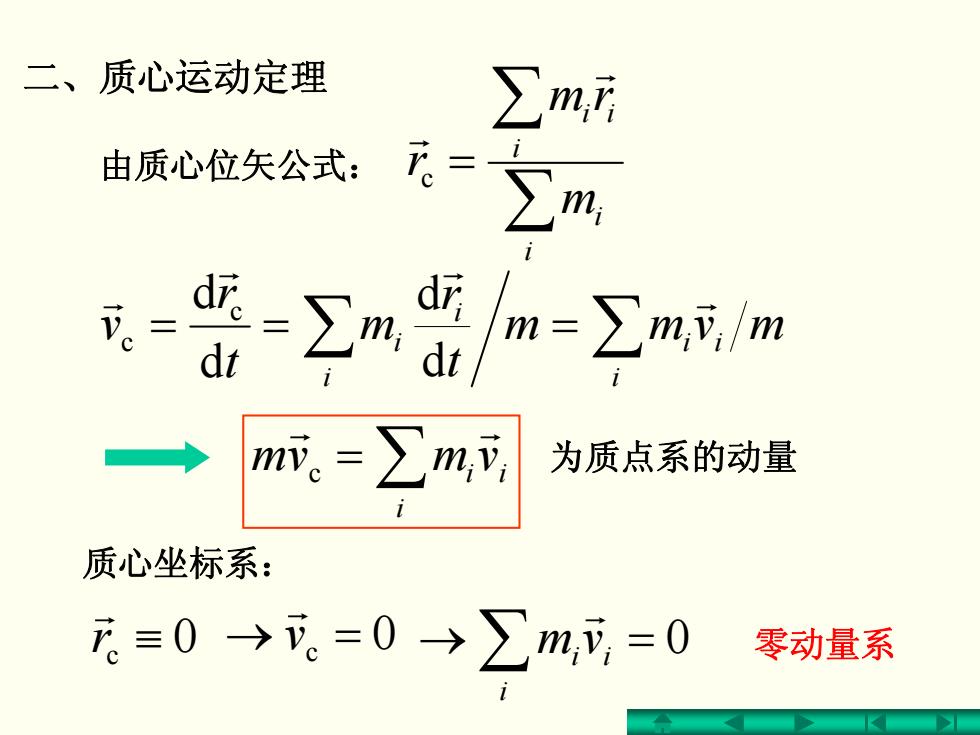
二、质心运动定理 ∑m 由质心位矢公式: 币。二 ∑m d m=∑m,/m m。=∑m,g 为质点系的动量 质心坐标系: 尼≡0→。=0→∑m,可=0 零动量系
二、质心运动定理 == ∑ ∑= i i ii i i mvmm t r m t r v r r r r d d d d c c i i ivmvm r r c = ∑ ∑ ∑ = i i i ii m rm r r r c 为质点系的动量 零动量系 质心坐标系: 由质心位矢公式: 0 rc ≡ r 0 → vc = r ∑ =→ 0 i i ivm r

由质点系动量定理: ∑fdt=∑%可-∑m。=成,-mi.o0 微分形式: ∑Fdt=mdi i=1 ∑=m dr 质心运动定理:质心的运动等同于一个质点的运动,这 个质点具有质点系的总质量,它受到的外力为质点系所 受的所有外力的矢量和
c c d d am t v mF i i r r r ∑ == 由质点系动量定理: c 1 dd vmtF i i r r ∑ = = 0 d 0 i i i i i i t t i i vmvmtF r r r ∫ ∑ −= ∑∑ 质心运动定理: 质心的运动等同于一个质点的运动,这 个质点具有质点系的总质量,它受到的外力为质点系所 受的所有外力的矢量和。 微分形式: 0cc vmvm r r = −

说明< 1.适用于惯性系。 2.∑=0,。=0质心系是惯性系, ∑,≠0,a。≠0质心系是非惯性系。 3.动量守恒、功能原理、角动量定理在质心系中成立。 4.质点系相对惯性系的运动可分解成: 随质心的运动+相对质心的运动。 质点系在实验室系的总动能: -Σm2” 资用能
1. 适用于惯性系。 0, 0 ∑ aF c ≠≠ i i r r 质心系是惯性系, 质心系是非惯性系。 0, 0 ∑ aF c == i i r r 2. 3. 动量守恒、功能原理、角动量定理在质心系中成立。 4. 质点系相对惯性系的运动可分解成: 随质心的运动+相对质心的运动。 2 2 c 2 2 1 2 1 2 1 ii i i ii i i = +∑∑∑ vmvmvm ′ 资用能 说明 质点系在实验室系的总动能:
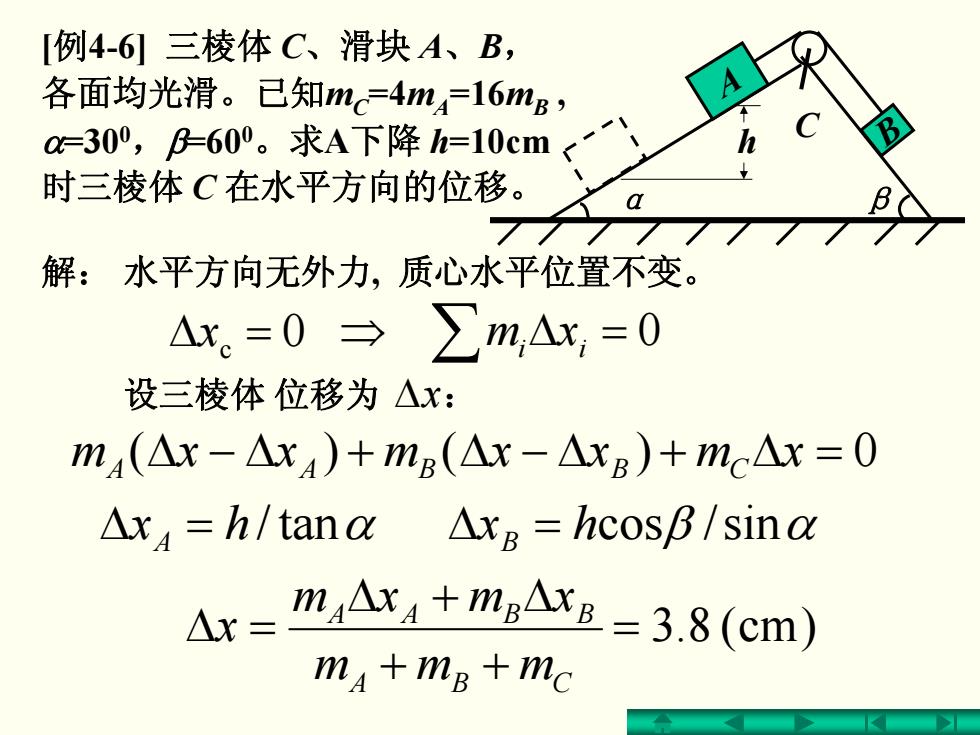
[例4-6]三棱体C、滑块A、B, 各面均光滑。已知nc=4m416mg, a=30,B-60°。求A下降h=10cm< 时三棱体C在水平方向的位移。 解:水平方向无外力,质心水平位置不变。 △x。=0→∑m,Ax,=0 设三棱体位移为△x: m4(△x-△xA)+m(△x-△xB)+mc△x=0 △x4=h/tana△xe=hcosB/sina ΛX= m△x4+mgAXB=3.8(cm) ma+mB +mc
[例4-6] 三棱体 C、滑块 A、B, 各面均光滑。已知mC=4mA=16mB , α=300,β=600。求A下降 h=10cm 时三棱体 C 在水平方向的位移。 解: Δ Δ− + Δ − Δ + Δxmxxmxxm = 0)()( A BA CB 水平方向无外力, 质心水平位置不变。 A C B α β h hx α tan/ Δ A = = )cm(8.3 ++ Δ + Δ =Δ CBA BBAA mmm xmxm x 设三棱体 位移为 : Δx xc =Δ 0 ∑ =Δ⇒ 0 ii xm hx β α sin/cos Δ B =

[例4-7]质量为M的人,手里拿着质量为m的物体,此人用 与地平线成的速度y向前跳去,当他到达最高点时,把 物体以相对于自己以速度向后抛出,问由于物体的抛出 ,他跳过的距离与不抛物体时相比可增加多少? 解法一」取地面坐标系,用动量守恒定律求解。 人不向后抛出物体,所跳 mM 过的距离: R 2v sinacosa 8 人在最高点向后抛出物体的过 程中,应用动量守恒定律: RR+△R MV+m(v-u)=(m+M)vo cosa
[例4-7] 质量为M的人,手里拿着质量为m的物体,此人用 与地平线成α 的速度v0 向前跳去,当他到达最高点时,把 物体以相对于自己以速度 u 向后抛出,问由于物体的抛出 ,他跳过的距离与不抛物体时相比可增加多少? 人不向后抛出物体,所跳 过的距离: [解法一] 取地面坐标系,用动量守恒定律求解。 人在最高点向后抛出物体的过 程中,应用动量守恒定律: g v R cossin2 αα 20 = + − = + vMmuVmMV 0 cos)()( α m M α R R+ΔR x y u r V r O