
第章质点运动定律 §2.1牛顿运动定律 一、牛顿三定律 二、相互作用与力 三、牛顿定律应用 §2.2力学相对性原理非惯性参考系 一、惯性参照系和非惯性参考系 二、力学相对性原理 三、平动加速参考系中的惯性力 四、惯性离心力
§2.1 牛顿运动定律 第 2 章 质点运动定律 §2.2 力学相对性原理 非惯性参考系 一、惯性参照系和非惯性参考系 一、牛顿三定律 二、相互作用与力 三、牛顿定律应用 二、力学相对性原理 三、平动加速参考系中的惯性力 四、惯性离心力

§2.2力学相对性原理非惯性参考系 一、惯性参考系和非惯性参考系 考虑如下两个参考系S(地面)和S'(相对于S加 速运动的车厢):车厢光滑底面上有一个滑块。 [SI 很显然在S参考系中,滑块的运动符合牛顿定律。 而在S参考系中则不然。 牛顿定律只在特殊的参照系—惯性系中成立! 牛顿定律不能成立的参照系一非惯性系
§2.2 力学相对性原理 非惯性参考系 牛顿定律只在特殊的参照系——惯性系中成立! 很显然在 S 参考系中,滑块的运动符合牛顿定律。 而在 S′参考系中则不然。 一、惯性参考系和非惯性参考系 [S] a r [S′] a' r 考虑如下两个参考系 S(地面)和 S′(相对于 S 加 速运动的车厢):车厢光滑底面上有一个滑块。 牛顿定律不能成立的参照系——非惯性系

实际上,没有严格意义上的惯性系存在,惯性系只是 参考系的一个理想物理模型。 实际工作中常常根据具体情况选用一些近似惯性系。 比如在研究地面上物体的运动时,选用地面参考系就 是一个很好的近似。 常用近似惯性系 地面参考系 地球自转加速度 a≈0.034m/s2 地心参考系 地球公转加速度 a≈0.006m/s2 太阳参考系 太阳绕银河系中心加速度 a≈3×10-10m/s2
地面参考系 地心参考系 太阳参考系 常用近似惯性系 地球自转加速度 a ∼ 0.034 m/s2 太阳绕银河系中心加速度 a ∼ 3 × 10 –10 m/s2 地球公转加速度 a ∼ 0.006 m/s2 实际上,没有严格意义上的惯性系存在,惯性系只是 参考系的一个理想物理模型。 实际工作中常常根据具体情况选用一些近似惯性系。 比如在研究地面上物体的运动时,选用地面参考系就 是一个很好的近似
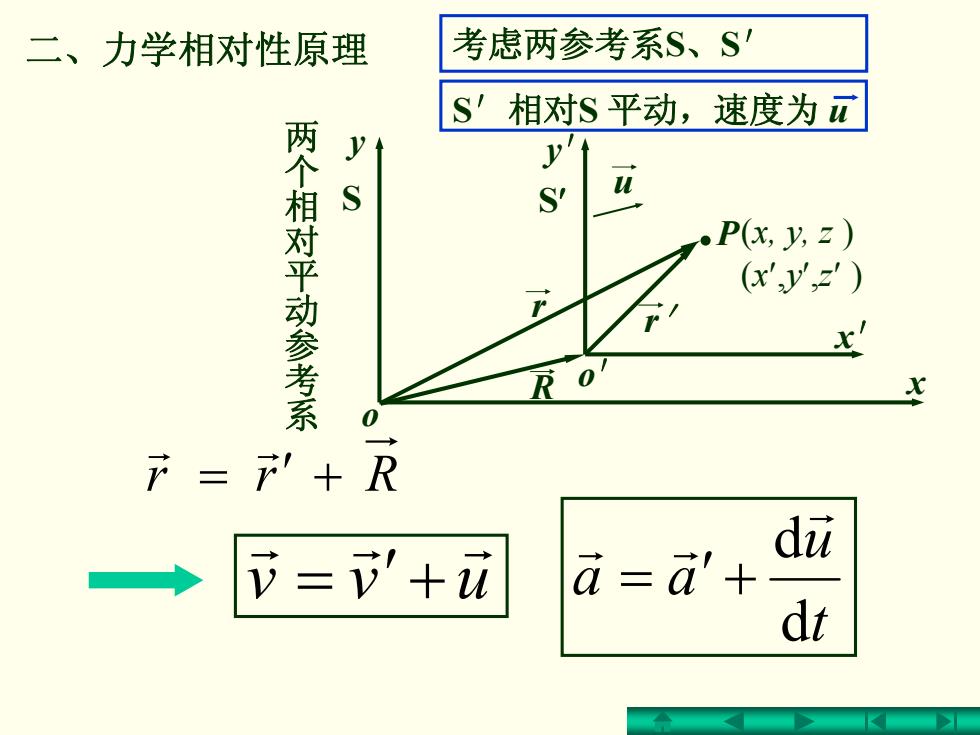
二、力学相对性原理 考虑两参考系S、S S'相对S平动,速度为五 y y 两个相对平动参考系 S ●P(xy,z) (x'y,z') x F01 ”+R du v=”+元 a= '+ dt
二、力学相对性原理 = ′ + Rrrr r t u aa d d r rr uvv = ′ + r r r = ′ + 考虑两参考系 S 、 S′ 两个相对平动参考系 S′相对 S 平动,速度为 u o r r ′ . P R o′ x x′ y y′ S S′ u (x, y, z ) (x′,y′,z′ )
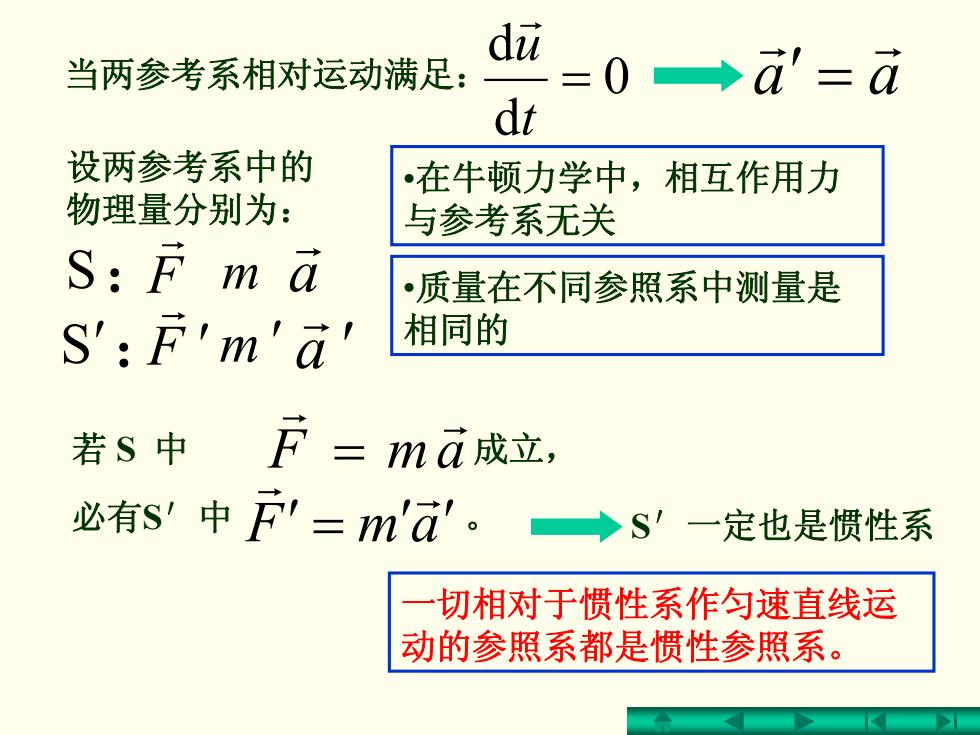
du 当两参考系相对运动满足: =0→a'=d dt 设两参考系中的 •在牛顿力学中,相互作用力 物理量分别为: 与参考系无关 S:F m a •质量在不同参照系中测量是 S':F'm'a' 相同的 若S中 = ma成立, 必有s'中F'=m'。 ◆S'一定也是惯性系 切相对于惯性系作匀速直线运 动的参照系都是惯性参照系
当两参考系相对运动满足: 0 d d = t u r aar r ′ = S : F r m a r F ′ r S ′ : m ′ a ′ r •在牛顿力学中,相互作用力 与参考系无关 •质量在不同参照系中测量是 相同的 amF r r 若 S 中 成 = 立 , ′ = amF ′′ r r 必有 S′中 。 S′一定也是惯性系 一切相对于惯性系作匀速直线运 动的参照系都是惯性参照系。 设两参考系中的 物理量分别为:

换句话说:牛顿定律在所有惯性系中均成立 且具有相同的形式。 力学相对性原理! 又可表述为:不可能通过惯性系内部进行任何形式的力 学实验来确定该惯性系相对于其它惯性系 的速度。 切惯性系在力学意义上是等价的,平权的!
一切惯性系在力学意义上是等价的,平权的! 力学相对性原理! 换句话说:牛顿定律在所有惯性系中均成立 且具有相同的形式。 又可表述为:不可能通过惯性系内部进行任何形式的力 学实验来确定该惯性系相对于其它惯性系 的速度

三、平动加速参考系中的惯性力 设S为惯性系,S'为非惯性系 du S'相对于S加速度为:( dt 两个平动参考系之间,加速度变换 a=a'+ao 若质点m在S系中满足牛顿第二定律:F=ma 考虑到力与参考系无关 FaF 则在s'系中:F≠md mao ma 牛顿第二定律在非惯性系不成立!
三、平动加速参考系中的惯性力 两个平动参考系之间,加速度变换 0 ' aaar r r = + 设 S 为惯性系,S ' 为非惯性系 若质点 m 在 S 系中满足牛顿第二定律: amF r r = t u a d d 0 r r S ' 相对于 S 加速度为: = 考虑到力与参考系无关 则在 S ' 系中: amF '' r r ≠ 牛顿第二定律在非惯性系不成立! FFr r '≡ ' 0 amamr r = +

但是,若在非惯性系引入 虚拟力(惯性力): F=-mdo 在非惯性系S'系中: F+F=ma' 牛顿第二定律在非惯性系 形式上成立 >惯性力不是真正作用在物体上的力! 考虑到力与参考系无关 ≡F 则在s'系中:F'≠ma mao ma 牛顿第二定律在非惯性系不成立!
但是,若在非惯性系引入 虚拟力(惯性力): I amF 0 r r −= ' I 在非惯性系 S ' 系中: amFF r r r =+ 牛顿第二定律在非惯性系 形式上成立 ¾惯性力不是真正作用在物体上的力! 考虑到力与参考系无关 则在 S ' 系中: amF '' r r ≠ 牛顿第二定律在非惯性系不成立! FFr r '≡ ' 0 amamr r = +

注意:惯性力不是真正作用在物体上的力! 惯性力无施力者,也无反作用力。 [S] 箱内光滑平台上的小球在两 个参考系中的运动描述。 S为惯性系,S为非惯性系 两个参考系相对加速度为d 在惯性系的观测者看来,惯 性力是真正的质点惯性的表 现!
注意:惯性力不是真正作用在物体上的力! 惯性力无施力者,也无反作用力。 在惯性系的观测者看来,惯 性力是真正的质点惯性的表 现! [S] [S] 箱内光滑平台上的小球在两 个参考系中的运动描述。 S 为惯性系, S′为非惯性系 两个参考系相对加速度为 a 0 r [S′] [S′] a 0 r [S′] [S′] a 0 r −
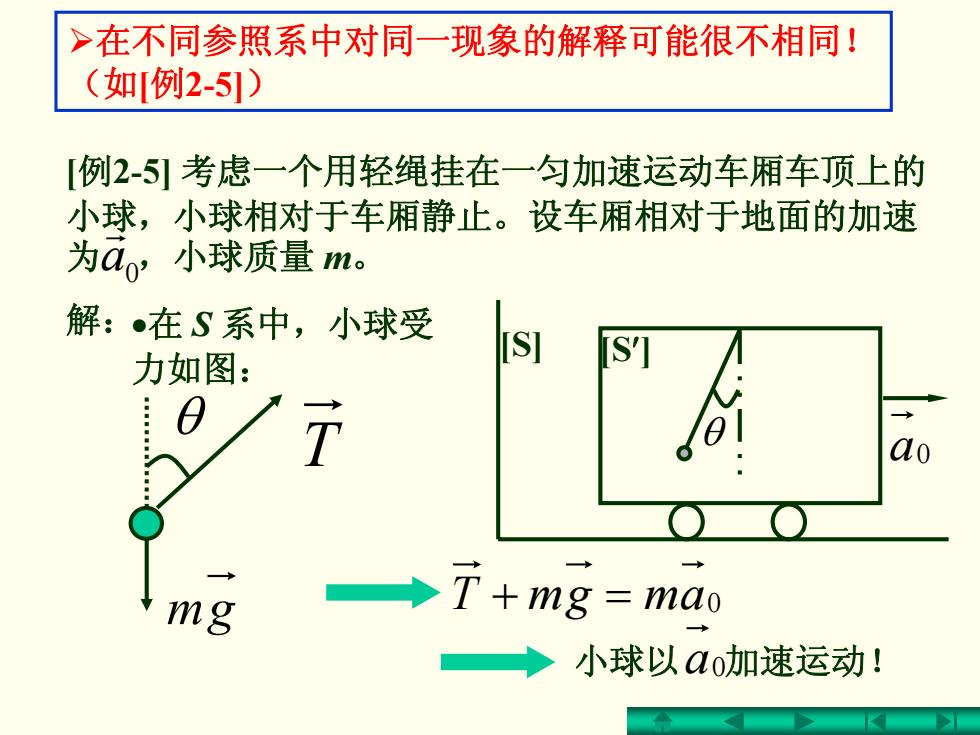
>在不同参照系中对同一现象的解释可能很不相同! (如例2-51) [例25]考虑一个用轻绳挂在一匀加速运动车厢车顶上的 小球,小球相对于车厢静止。设车厢相对于地面的加速 为a,小球质量m。 解:在S系中,小球受 力如图: ao mg →T+mg=mao ◆小球以☑o加速运动!
解: ¾在不同参照系中对同一现象的解释可能很不相同! (如[例2-5]) gm T θ =+ amgmT 0 [S] [S′] a0 θ [例2-5] 考虑一个用轻绳挂在一匀加速运动车厢车顶上的 小球,小球相对于车厢静止。设车厢相对于地面的加速 为 ,小球质量 a0 m。 r 小球以 加速运动! a0 •在 S 系中,小球受 力如图: