
第12章导体电学 §12.1导体的静电平衡性质 §12.2空腔导体 §12.3电容及电容器 §12.4传导电流 §12.5电源及稳恒电流
第 12 章 导体电学 §12.1 导体的静电平衡性质 导体的静电平衡性质 §12.2 空腔导体 §12.3 电容及电容器 §12.4 传导电流 §12.5 电源及稳恒电流 电源及稳恒电流

§12.2空腔导体 本节讨论如图所示有空腔的导 体与静电场的相互作用问题。 ● 包括: (1)空腔导体上的电荷分布特征。 (2)空间电场分布特征
§12.2 空腔导体 包括: (1)空腔导体上的电荷分布特征。 (2)空间电场分布特征。 本节讨论如图所示有空腔的导 体与静电场的相互作用问题。 . q
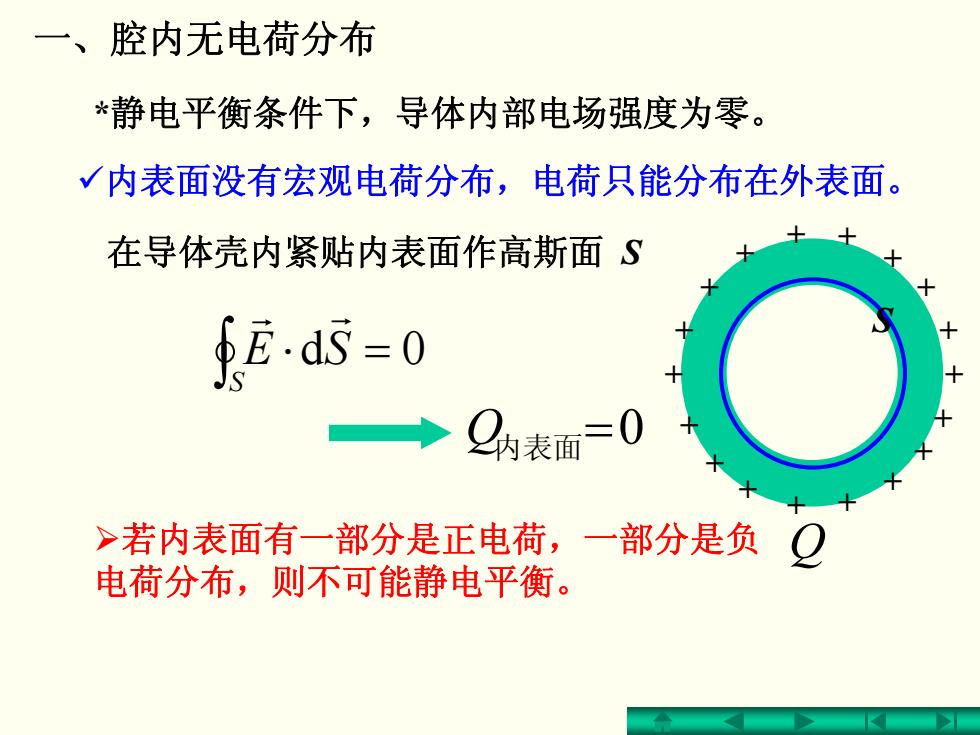
一、腔内无电荷分布 *静电平衡条件下,导体内部电场强度为零。 内表面没有宏观电荷分布,电荷只能分布在外表面。 在导体壳内紧贴内表面作高斯面S fE.d5-0 →Q纳表面=0 >若内表面有二部分是正电荷,一部分是负Q 电荷分布,则不可能静电平衡
S =⋅ 0d ∫S SEr r 一、腔内无电荷分布 9内表面没有宏观电荷分布,电荷只能分布在外表面。 在导体壳内紧贴内表面作高斯面 S Q内表面=0 ¾若内表面有一部分是正电荷,一部分是负 电荷分布,则不可能静电平衡。 + + + + + + + + + + + + + + + + + + Q *静电平衡条件下,导体内部电场强度为零

√腔内无电场 即E腔内=0 或说,腔内电势处处相等。 证明:在导体腔内任选一等势面为 高斯面S,利用高斯定理: E.ds=fEds=0 →E腔内三0
E腔内 = 0 或说,腔内电势处处相等。 即 9腔内无电场 证明:在导体腔内任选一等势面为 高斯面 S,利用高斯定理: ∫ ⋅ S SEr r d E腔内 ≡ 0 ∫ = S dSE = 0 S

二、腔内有电荷分布(g和腔体带电Q) 电荷分布 (1)( 腔内表面=一9用高斯定理可以证明 (2)Q外表面=9+Q电荷守恒定律! Q+9 ·腔内的电场由q和腔内表面的感应电荷-q共同决 定,与腔内电荷位置、腔体的几何结构有关。 >由唯一性定理和平衡条件可以证明上述及下述结论。 ·导体腔外部电场由外表面电荷分布σ确定;与腔内电 荷及腔内表面感应电荷无关。 它管外装面 O外表面e, 60
二、腔内有电荷分布( q和腔体带电 Q ) • 电荷分布 腔内表面 = −qQ 用高斯定理可以证明! 腔外表面 = +QqQ • 腔内的电场由 q 和腔内表面的感应电荷 -q 共同决 定,与腔内电荷位置、腔体的几何结构有关。 • 导体腔外部电场由外表面电荷分布 σ 确定;与腔内电 荷及腔内表面感应电荷无关。 n 0 E e r r ε σ 外表面 腔外表面 = ¾由唯一性定理和平衡条件可以证明上述及下述结论。 ( 2 ) 电荷守恒定律! ( 1 ) q - - - - - - - - - --- - - - - - - − q + + + + + + + + + + + + + + + + + + + qQ

三、静电屏蔽的装置 根据导体腔的电学性质;可以利用空腔导体对腔内、 外进行静电隔离。 (1)空腔导体起到屏蔽 外电场的作用。 仪器
(1)空腔导体起到屏蔽 外电场的作用。 根据导体腔的电学性质;可以利用空腔导体对腔内、 外进行静电隔离。 - - -- - - 三、静电屏蔽的装置 仪器 + + + + + + + + + + + + +
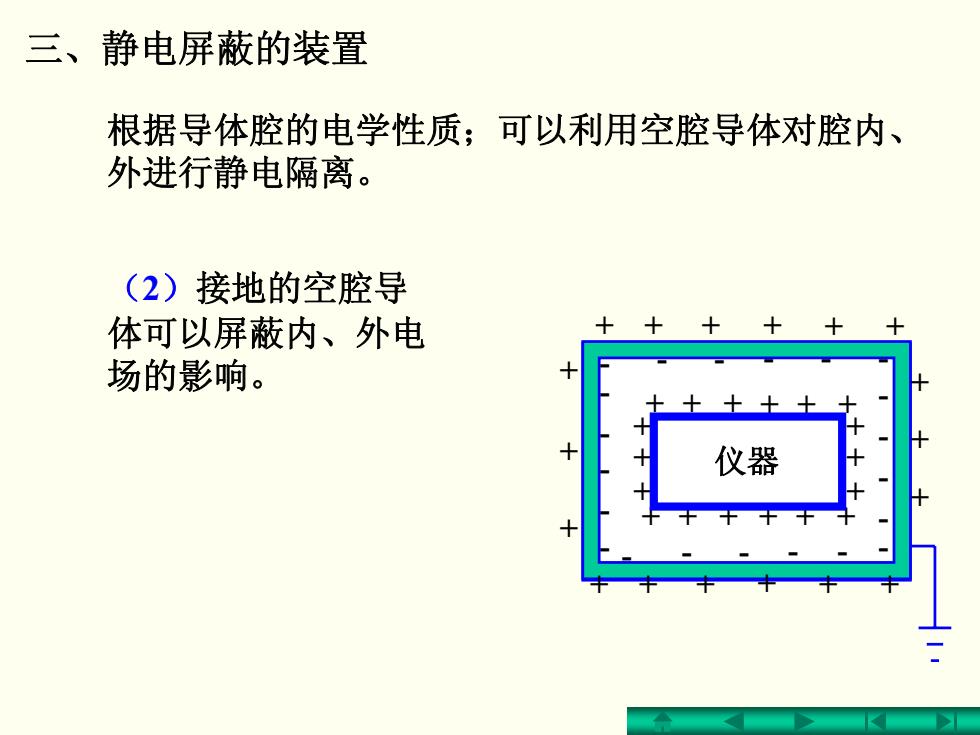
三、静电屏蔽的装置 根据导体腔的电学性质;可以利用空腔导体对腔内、 外进行静电隔离。 (2)接地的空腔导 体可以屏蔽内、外电 十十 十 十 十 场的影响。 仪器
(2)接地的空腔导 体可以屏蔽内、外电 场的影响。 - - - - - - - - -- - - - - - - - - - - - + + + + + + + + + + + + + + + + + + 仪器 + + + + + + + + + + + + + + + + + + 三、静电屏蔽的装置 根据导体腔的电学性质;可以利用空腔导体对腔内、 外进行静电隔离

[例题12-2金属球A与金属球壳B同 心放置。已知球A半径为R,带电 为q,金属壳B内外半径分别为R2, R3,带电为Q。求:(1)系统的电 荷分布(2)空间电势分布及球和壳 B的电势。 解:(1)静电平衡时,导体(净) 电荷只能分布在导体表面上。 •球A的电量只可能在球的表面。 壳B有两个表面,电量分布在内、外两个表面。 •由于A、B对称中心重合,电荷及场分布应该对 该中心是球对称。 >电荷在导体表面均匀分布
[例题12-2]金属球A与金属球壳B同 心放置。已知球A半径为R1,带电 为q,金属壳B内外半径分别为R2, R3,带电为Q。求:(1)系统的电 荷分布(2)空间电势分布及球A和壳 B的电势。 A B q Q 解:(1)静电平衡时,导体(净) 电荷只能分布在导体表面上。 •球A的电量只可能在球的表面。 •壳B有两个表面,电量分布在内、外两个表面。 •由于A、B对称中心重合,电荷及场分布应该对 该中心是球对称。 ¾电荷在导体表面均匀分布

按照高斯定理和电荷守恒定律, 电荷分布如图所示。 可以等效为:真空中三个中心 相互重合的均匀带电球面。 球A的电量只可能在球的表面。 壳B有两个表面,电量分布在内、外两个表面。 •由于A、B对称中心重合,电荷及场分布应该对 该中心是球对称。 >电荷在导体表面均匀分布
•球A的电量只可能在球的表面。 •壳B有两个表面,电量分布在内、外两个表面。 •由于A、B对称中心重合,电荷及场分布应该对 该中心是球对称。 ¾电荷在导体表面均匀分布 + + + + + + + + + + + + +qQ −q - - - - - - - - q + + + + + + + + 按照高斯定理和电荷守恒定律, 电荷分布如图所示。 可以等效为:真空中三个中心 相互重合的均匀带电球面

(2)利用叠加原理求电势 Q+q V -q Q+9 4元8o ” 4π6o' 4元8o 0+q 4π8o' -9 *ATERe Q+9 4元8or ,4π8R3 →V= Q+9 VB=V7,-R,=4π&R *同样办法可以得到各个区域内的电场分布。 *注意外球壳接地时的电荷分布和电场分布情况
(2)利用叠加原理求电势 r q VI π 0 4 ε = r q π 0 4 ε − + r qQ π 0 4 ε + + −q q +qQ O⋅R1 R2 R3 I II r qQ π 0 4 ε + = r q VII π 0 4 ε = π 30 3 4 R qQ VV Rr IB ε+ == = π 20 4 R q ε − + π 30 4 R qQ ε + + Rr 1 VV IIA = = *同样办法可以得到各个区域内的电场分布。 *注意外球壳接地时的电荷分布和电场分布情况