
第12章导体电学 §12.1导体的静电平衡性质 §12.2空腔导体 §12.3电容及电容器 §12.4传导电流 §12.5电源及稳恒电流
第 12 章 导体电学 §12.1 导体的静电平衡性质 导体的静电平衡性质 §12.2 空腔导体 §12.3 电容及电容器 §12.4 传导电流 §12.5 电源及稳恒电流 电源及稳恒电流

§12.3电容及电容器 一、孤立导体的电容 孤立导体的电势与带电量有关;带电量相同时不同 形状和大小的孤立导体电势不同,但是VQ。 定义C 孤立导体的电容 电容只与导体的几何因素(及周围介质)有关,反 映导体带电多少的本领一 固有的容电本领。 SI:F(法拉) 1F=10uF=102pF
§12.3 电容及电容器 一、孤立导体的电容 电容只与导体的几何因素(及周围介质)有关,反 映导体带电多少的本领——固有的容电本领。 SI:F(法拉) ∝ QV 孤立导体的电势与带电量有关; V Q 定义 C ≡ ——孤立导体的电容 10F1 μ pF10F 6 12 == 带电量相同时不同 形状和大小的孤立导体电势不同,但是

***真空中孤立导体球的电容** 设导体球半径为R,带电为Q。 导体球电势为: V= 4π6,R 导体球电容为: C= 9=4πE,R 对半径如地球一样的导体球,其电容为: CE=4πeRε=7.11×104F 电容为1F的孤立导体球的半径 R- -=8.99×10m>>Re 4元80
π 0 4 1 ε R = m1099.8 9 ×= >> RE *** 真空中孤立导体球的电容*** R Q V 4π 0 ε = V Q C = 4π 0R 设导体球半径为R,带电为Q。 导体球电势为: 导体球电容为: = ε 电容为1F 的孤立导体球的半径 对半径如地球一样的导体球,其电容为: E π E0 = 4 ε RC F1011.7 −4 ×=

二、电容器的电容 一般情况下,导体并不是孤立的,而是多个导 体组成的导体组—电容器。 基本单元:两导体组(A、B)电容器 (±2,△VB) 定义: △V AB >电容器电容只与导体组的几何构形(及周围空间介 质)有关,与带电多少无关一固有的容电本领。 >电容器电容的计算步骤 设电容器带电±2,求两个极板的电势差△V4B, 按定义求C
二、电容器的电容 V AB Q C Δ 定义: = 一般情况下,导体并不是孤立的,而是多个导 体组成的导体组——电容器。 基本单元:两导体组(A、B)电容器 ) ,(± ΔVQ AB 设电容器带电±Q,求两个极板的电势差ΔVAB, 按定义求C。 ¾电容器电容只与导体组的几何构形(及周围空间介 质)有关,与带电多少无关——固有的容电本领。 ¾电容器电容的计算步骤
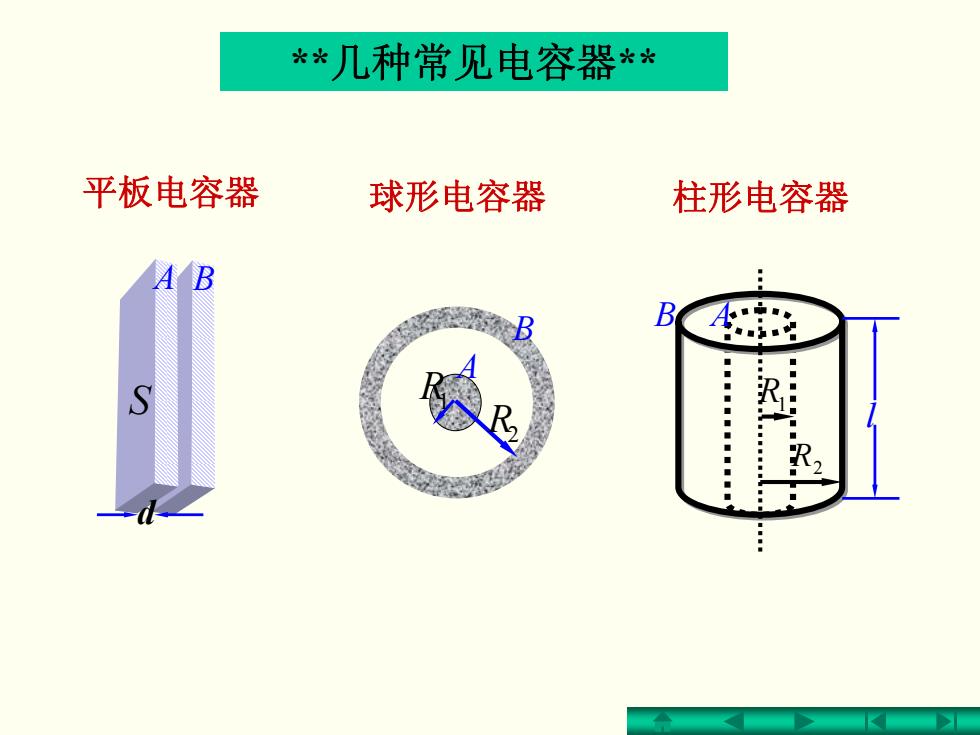
*几种常见电容器* 平板电容器 球形电容器 柱形电容器 B
**几种常见电容器** 球形电容器 R1 R2 B A 平板电容器 d S A B 柱形电容器 R1 R2 B A l
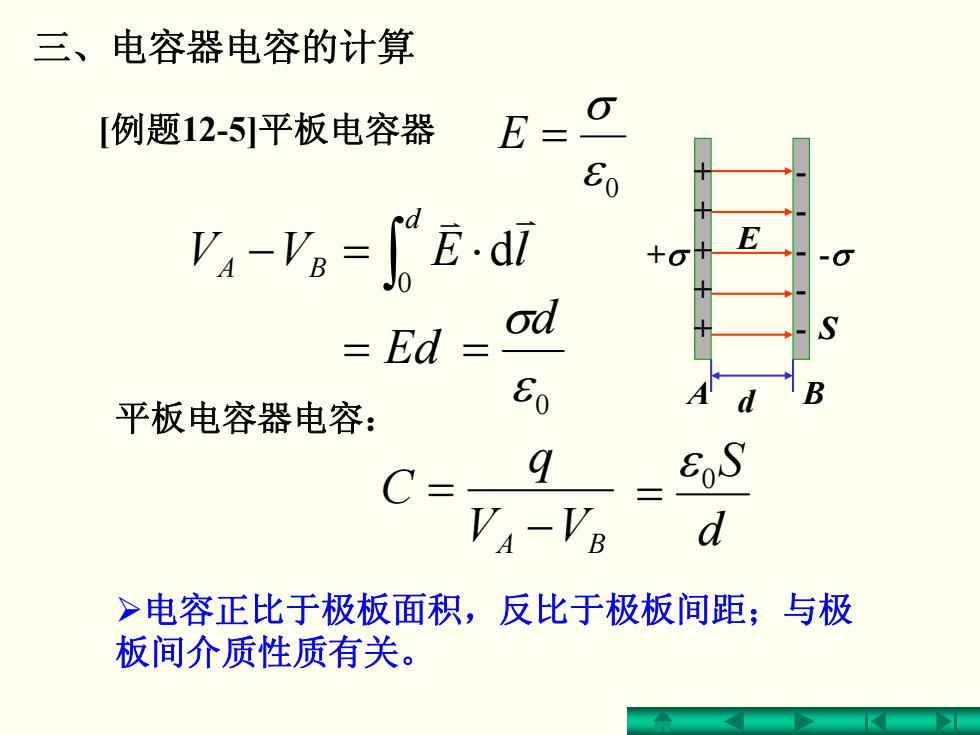
三、电容器电容的计算 [例题12-5]平板电容器 0 E= 80 Va-V。-Edl E +o od Ed d 平板电容器电容: Eo C= q VA-VB >电容正比于极板面积,反比于极板间距;与极 板间介质性质有关
三、电容器电容的计算 [例题12-5]平板电容器 + + + + + - - - - - d BA + σ - σ E S 0 ε σ E = ∫ ⋅=− d BA lEVV 0 d v v VV BA q C − = = Ed 0 ε σd = d S 0 ε = 平板电容器电容: ¾电容正比于极板面积,反比于极板间距;与极 板间介质性质有关

[例题12-6]求柱形电容器单位长度的电容。 解: 设单位长度带电量为±入 E= 2π8,r -er R<r<R r元_e,…di _dr C= 2元E0 △V 2元80 R R
[例题12-6]求柱形电容器单位长度的电容。 设单位长度带电量为 ± λ e r r E π 0 2 ε λ = ∫ =Δ ⋅ 外 内 le r V r d 2 π 0 ε λ V C Δ = λ 1 2 0 ln 2 π R R ε λ = 1 < < RrR 2 解: 1 2 0 ln 2 π R R ε = ∫ = 2 1 d 2 π 0 R R r ε r λ l 1 R 2 R

[例题12-71球形电容器电容。 解:E= s →C=9=4mR-R RARB END
[例题12-7]球形电容器电容。 er r q E 2 π 0 4 ε = ∫ =Δ BARR rrq V 2 π 0 4 dε V q C Δ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ = − RR BA q 11 4π 0 ε AB BA RR RR − = π 0 4 ε 解: END RA RB q - - - - - - - - +q + + + + + + +