
第12章导体电学 §12.1导体的静电平衡性质 §12.2空腔导体 §12.3电容及电容器 §12.4传导电流 §12.5电源及稳恒电流
第 12 章 导体电学 §12.1 导体的静电平衡性质 导体的静电平衡性质 §12.2 空腔导体 §12.3 电容及电容器 §12.4 传导电流 §12.5 电源及稳恒电流 电源及稳恒电流

§12.4传导电流 一、 电流 电流是由于电荷移动引起的,有以下两类基 本的形成电流的物理机制: 1.传导电流 (1)金属中的自由电子在外电场的作用下的宏观定 向移动。 (2)电解质溶液或电离气体中正、负离子的宏观 定向移动。 2.运流电流 单个或多个电荷在空间的定向移动(或运动)。 如:分子中电子绕核的运动,等效为圆电流。 分子的等效电流称为分子电流或安培电流
§12.4 传导电流 一、电流 1. 传导电流 (1)金属中的自由电子在外电场的作用下的宏观定 向移动。 (2)电解质溶液或电离气体中正、负离子的宏观 定向移动。 2. 运流电流 单个或多个电荷在空间的定向移动(或运动)。 如:分子中电子绕核的运动,等效为圆电流。 分子的等效电流称为分子电流或安培电流。 电流是由于电荷移动引起的,有以下两类基 本的形成电流的物理机制:

二、电流强度 大小:单位时间内通过导体某一截面的电量 I-lim M g-dq _dt 方向:正电荷运动的方向 单位:A(安培) 若电流强度与时间无关一稳恒电流
二、电流强度 大小:单位时间内通过导体某一截面的电量 方向:正电荷运动的方向 单位: A(安培) t q I t Δ Δ = →Δ lim 0 t q d d = 若电流强度与时间无关——稳恒电流
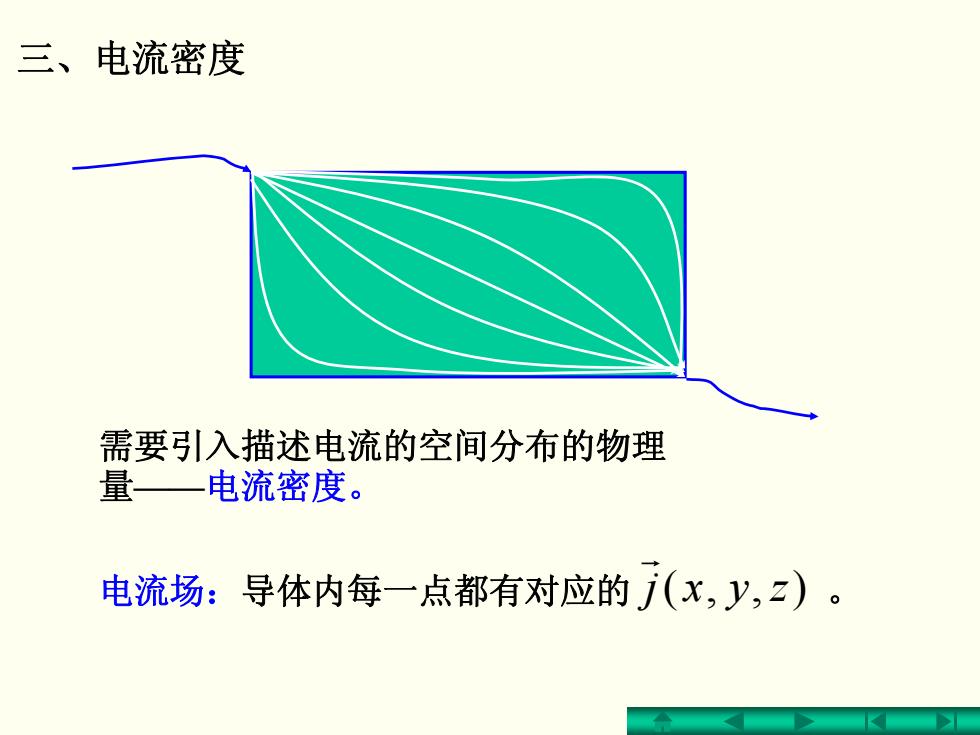
三、电流密度 需要引入描述电流的空间分布的物理 量一电流密度。 电流场:导体内每一点都有对应的(x,y,z)
三、电流密度 需要引入描述电流的空间分布的物理 量——电流密度。 电流场:导体内每一点都有对应的 zyxj ),,( 。 r
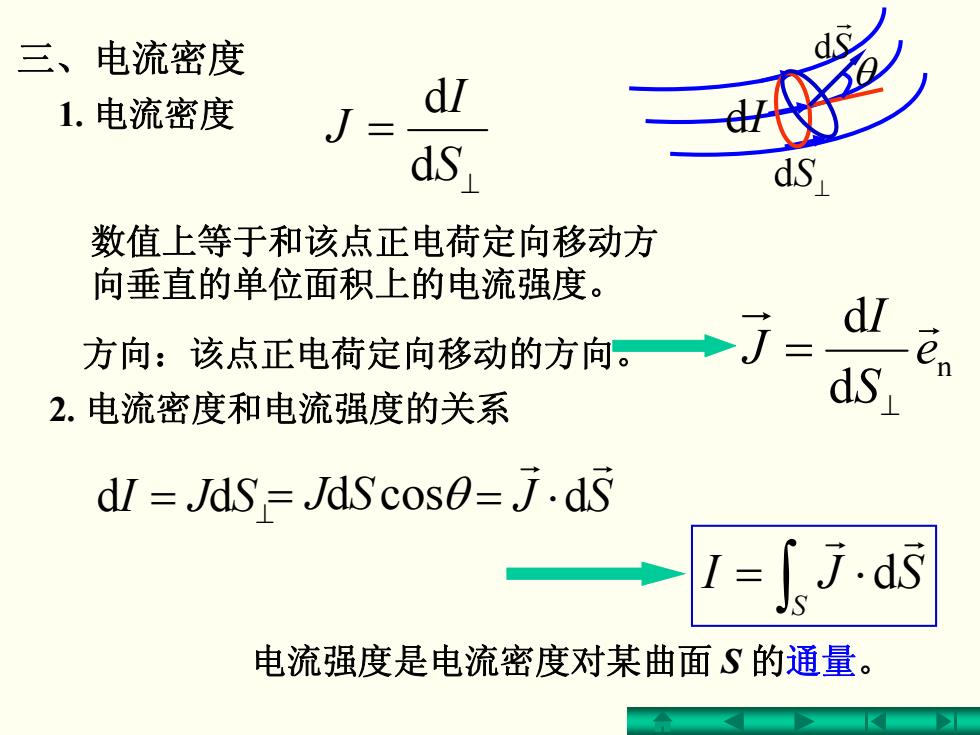
三、电流密度 1.电流密度 d d dS dS 数值上等于和该点正电荷定向移动方 向垂直的单位面积上的电流强度。 方向:该点正电荷定向移动的方向。→了 dl 2.电流密度和电流强度的关系 dS dI JdS=JdScos0=J.ds 电流强度是电流密度对某曲面S的通量
⊥ = S I J d d = dd SJI ⊥ 2. 电流密度和电流强度的关系 ∫ ⋅= S SJI r r d 数值上等于和该点正电荷定向移动方 向垂直的单位面积上的电流强度。 方向:该点正电荷定向移动的方向。 SJ r r ⋅= d n d d e S I J r ⊥ = θ = SJ cosd θ 电流强度是电流密度对某曲面 S 的通量。 1. 电流密度 三、电流密度 ⊥ dS S r d dI
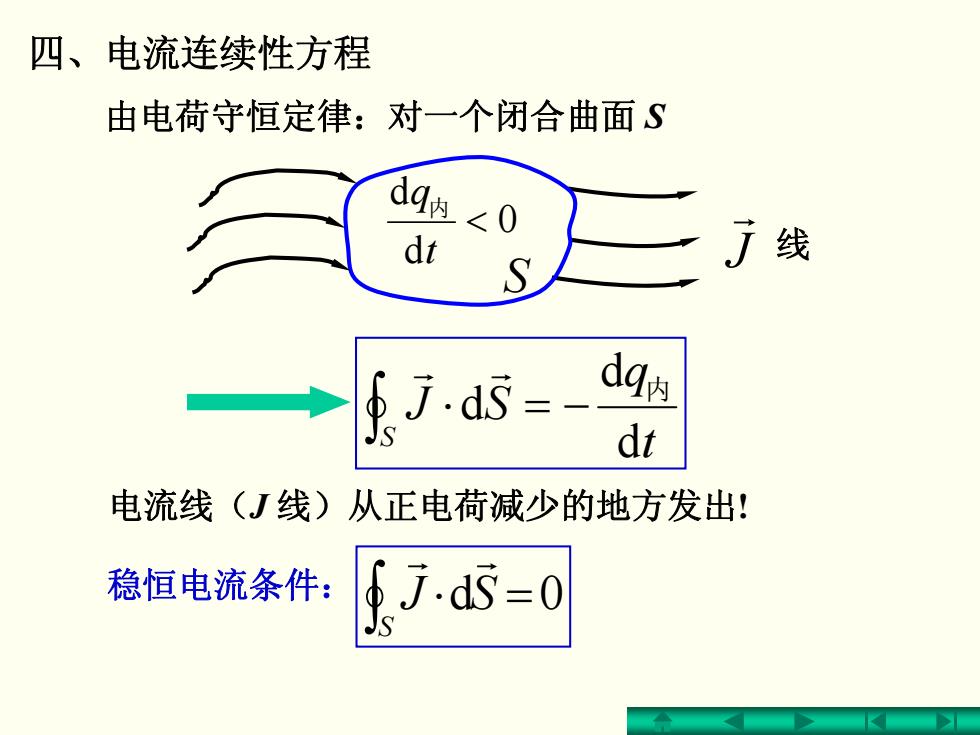
四、电流连续性方程 由电荷守恒定律:对一个闭合曲面S dq的 <0 dt 广线 dq内 dt 电流线(J线)从正电荷减少的地方发出: 稳恒电流条件: fJ-d5-o
四、电流连续性方程 t q SJ S d d d 内 −=⋅ ∫ r r 电流线( J 线)从正电荷减少的地方发出! 由电荷守恒定律:对一个闭合曲面 S =⋅ 0d ∫S SJr r 稳恒电流条件: S J r 线 0 d d < t q 内
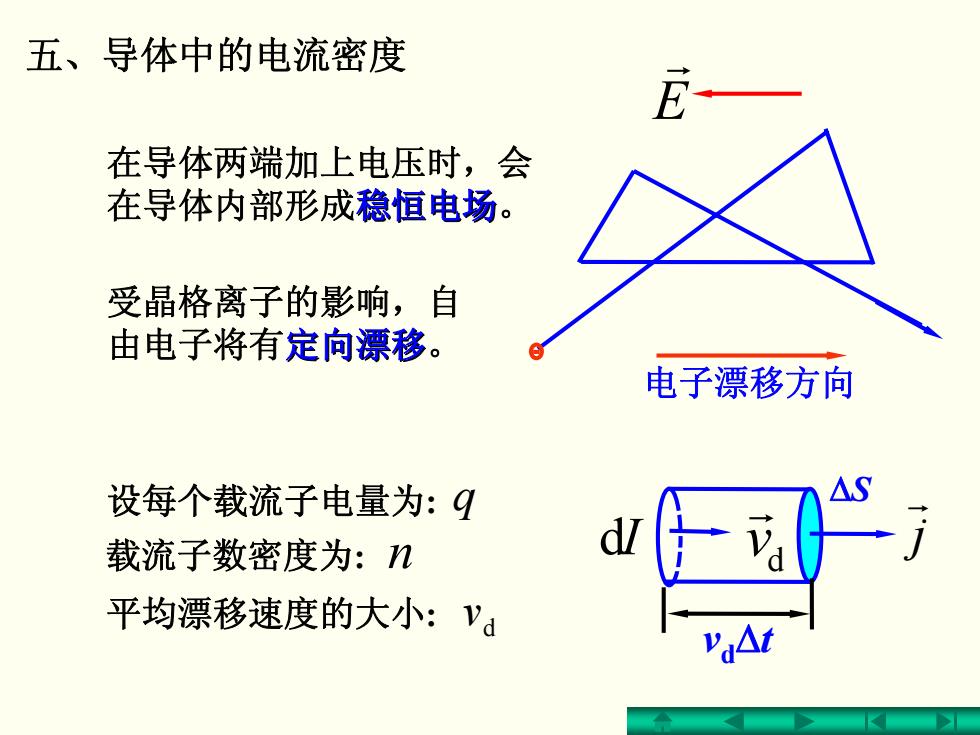
五、导体中的电流密度 E 在导体两端加上电压时,会 在导体内部形成稳恒电场。 受晶格离子的影响,自 由电子将有定向漂移。 电子漂移方向 设每个载流子电量为:q 载流子数密度为:n 平均漂移速度的大小:V
五、导体中的电流密度 在导体两端加上电压时,会 在导体内部形成稳恒电场 。 受晶格离子的影响,自 由电子将有定向漂移 。 设每个载流子电量为: q 载流子数密度为: n 平均漂移速度的大小: d v 电子漂移方向 E r v d Δ t ΔS d v r j r dI

d/= q[n(va△tS)] △t =qnva△S d ◆J= nqvd △S 矢量式 厅=ng。 (1)q>0,j与同向 (2)q<0,j与:反向 设每个载流子电量为:9 载流子数密度为:n 平均漂移速度的大小:Vd
t Stvnq I Δ Δ Δ = )]([ d d S I J Δ = d 矢量式 d vnqJ r = q > ,0 J d v r (1) 与 同向 = ΔSqnvd q < ,0 d vr (2) 与J 反向 = nqvd 设每个载流子电量为: q 载流子数密度为: n 平均漂移速度的大小: d v vdΔt ΔS d v r j r dI

六、欧姆定律的“微分形式” U dl +du 欧姆定律:dI=dU/R -dl ds 设导体内的稳恒电场为E,电子平均自由飞行时间为T 电子的平均漂移速度为:瓦。= m x~1×103(m/s) →j=ng= ngtE= 2m ng"t →Y= 一电导率 2m →j=呢 欧姆定律的微分形式
EJ r r = γ 六、欧姆定律的“微分形式” dI dS dl U U + dU 欧姆定律: dI = dU / R τ m qE v 2 d r r = d J nqvr = 电子的平均漂移速度为: 设导体内的稳恒电场为 E,电子平均自由飞行时间为τ E m nq r 2 2τ = E r ≡ γ ——欧姆定律的微分形式。 m nq 2 2τ ⇒ γ = ~ 1 10 (m/s) −3 × —电导率

U dl U+du E dS dl d au dl dS dl ldu 在常温下: d三Y dS- dl P:Po(1+at) (1)在极低温下,金属导 与欧姆定律相比: dS 体电阻消失—超导体。 d/= du (2)1980s中期,发现 R “高温”超导体(化合物超 dl R 导电性)。 三 rdS dS J=yE 电阻率 0 1/Y
)1( 0 t ρ t = ρ + α EJr r = γ R U I d d = , d d S I Q j = 与欧姆定律相比: E S I = γ d d l U E d d = S l U I d d d d = γ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = S l U d d d γ S l R d d γ = 电阻率 ρ = 1 / γ 在常温下: ( 1)在极低温下,金属导 体电阻消失——超导体 。 ( 2 )1980’s 中期,发现 “高温 ”超导体(化合物超 导电性)。 l U d d = γ S l d d ≡ ρ dI dS d l U U + d U