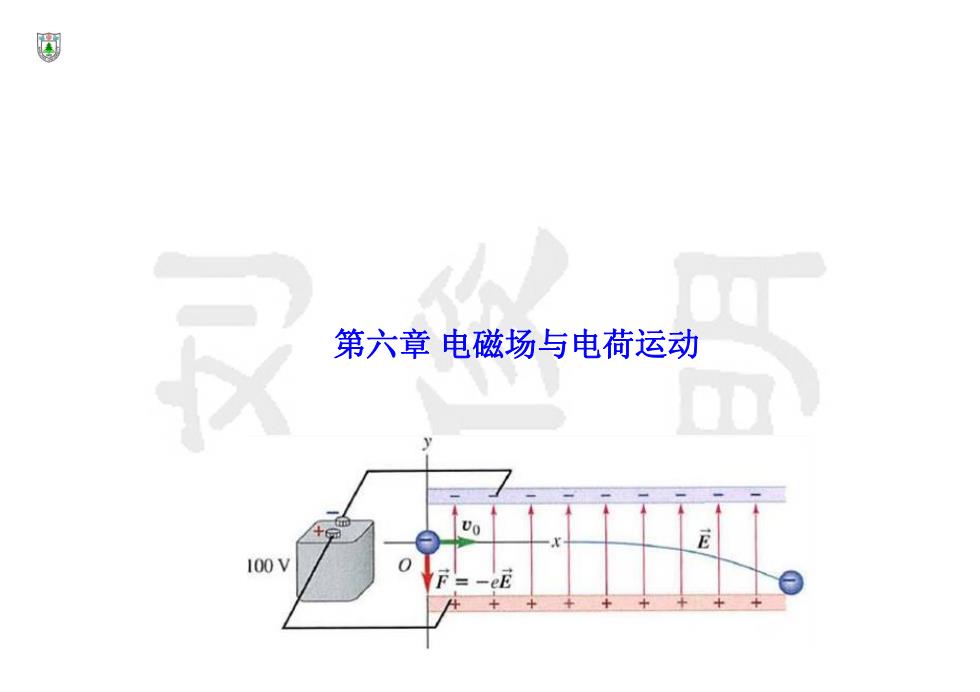
國 第六章电磁场与电荷运动 00 100V E
第六章 电磁场与电荷运动

电磁学06-01:从宏观到微观 q0 ▣电流在磁场中受力图: g=0 q>0 df Idl x B
电磁学06-01: 从宏观到微观 电流在磁场中受力图: df Idl B

厦电磁学06-01:从宏观到微观 Posltives Negatives 口电荷在电磁场中受力与运动: 口实验证明:运动电荷在磁场中受 力; ▣ 建立力F与q、w、B及/B夹角 0的关系: 又9啡0 F=qT×B 又k又Q ▣洛仑兹力做功吗? Stronger fleld grad HI 口洛仑兹力与安培力的关系? Weaker field DI元
电磁学06-01: 从宏观到微观 电荷在电磁场中受力与运动: 实验证明:运动电荷在磁场中受 力; 建立力 F 与 q、v、B 及 v/B 夹角 的关系: F qv B 洛仑兹力做功吗? 洛仑兹力与安培力的关系?

圆电磁学06-02:洛伦兹力与安培力的关系 口电子数密度为n,漂移速度u 口dl内总电子数为N=nSdl, 口每个电子受洛仑兹力f f=-euxB ▣N个电子所受合力总和是安培力吗? 口对象不同:洛伦兹力f作用在金属内的电子上,安培力作用在 导体金属上: ▣自由电子受力后,不会越出金属导线,而是将获得的冲量传递 给金属晶格骨架,使骨架受到力。 free charge lattice
电磁学06-02: 洛伦兹力与安培力的关系 电子数密度为 n,漂移速度 u dl内总电子数为 N=nSdl, 每个电子受洛仑兹力 f N 个电子所受合力总和是安培力吗? f eu B 对象不同:洛伦兹力 f 作用在金属内的电子上,安培力作用在 导体金属上; 自由电子受力后,不会越出金属导线,而是将获得的冲量传递 给金属晶格骨架,使骨架受到力。 free ch e lattice arg f f
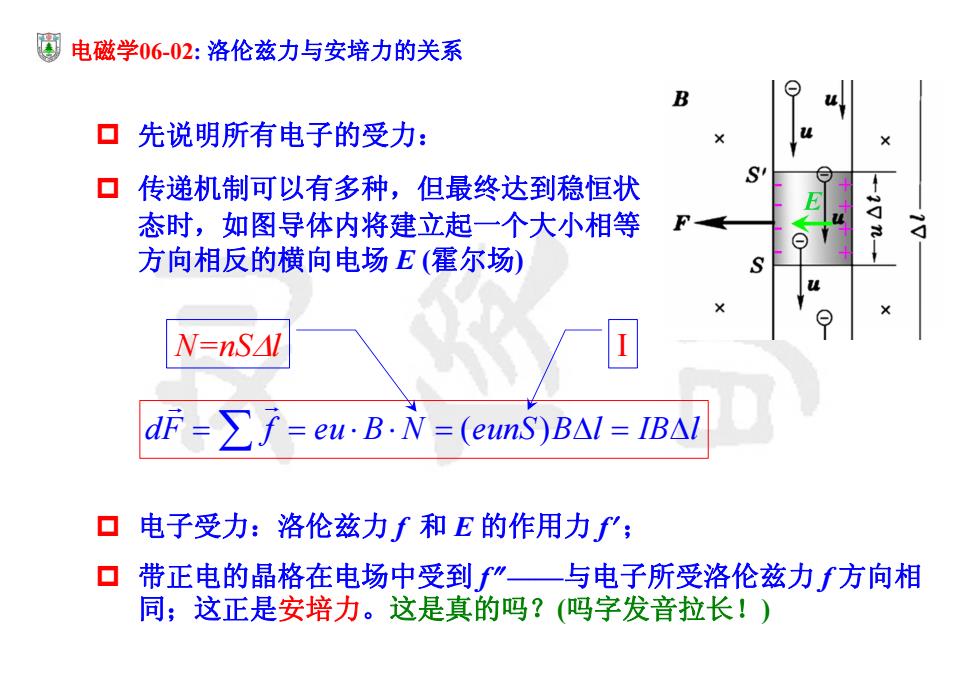
圜电磁学06-02:洛伦兹力与安培力的关系 B ▣先说明所有电子的受力: 口传递机制可以有多种,但最终达到稳恒状 态时,如图导体内将建立起一个大小相等 方向相反的横向电场E(霍尔场) + N=nSAl dF-∑f=e~B·N=(eunS)BAl=IBA1 ▣电子受力:洛伦兹力f和E的作用力f': 口带正电的晶格在电场中受到f”一与电子所受洛伦兹力方向相 同;这正是安培力。这是真的吗?(吗字发音拉长!)
电磁学06-02: 洛伦兹力与安培力的关系 先说明所有电子的受力: 传递机制可以有多种,但最终达到稳恒状 态时,如图导体内将建立起一个大小相等 方向相反的横向电场 E (霍尔场) dF f eu B N eunS B l IB l ( ) N=nSl I 电子受力:洛伦兹力 f 和 E 的作用力 f ; 带正电的晶格在电场中受到 f ——与电子所受洛伦兹力 f 方向相 同;这正是安培力。这是真的吗?(吗字发音拉长!)

圆电磁学06-02:洛伦兹力与安培力的关系 口再说明导线中自由电子与宏观电流的关系: > 自由电子做定向运动,漂移速度,电子数密 度为n >电流强度:单位时间内通过截面的电量 > 则在△时间内,通过导体内任一面元S迁移 的电量为 电流密度 △g=(u△t△S cos0)ne dl lim g_d9=ne:udSos6=(nea因 →0△tdt ▣ 安培力是晶格所带电荷受力”的总和,是电子所受洛伦兹力的 宏观表现
电磁学06-02: 洛伦兹力与安培力的关系 再说明导线中自由电子与宏观电流 I的关系: 自由电子做定向运动,漂移速度 u,电子数密 度为 n 电流强度 I:单位时间内通过截面的电量 则在 t 时间内,通过导体内任一面元 S 迁移 的电量为 0 ( cos ) lim cos t q u t S ne q dq dI ne udS neu dS t dt 电流密度 安培力是晶格所带电荷受力 f 的总和,是电子所受洛伦兹力的 宏观表现
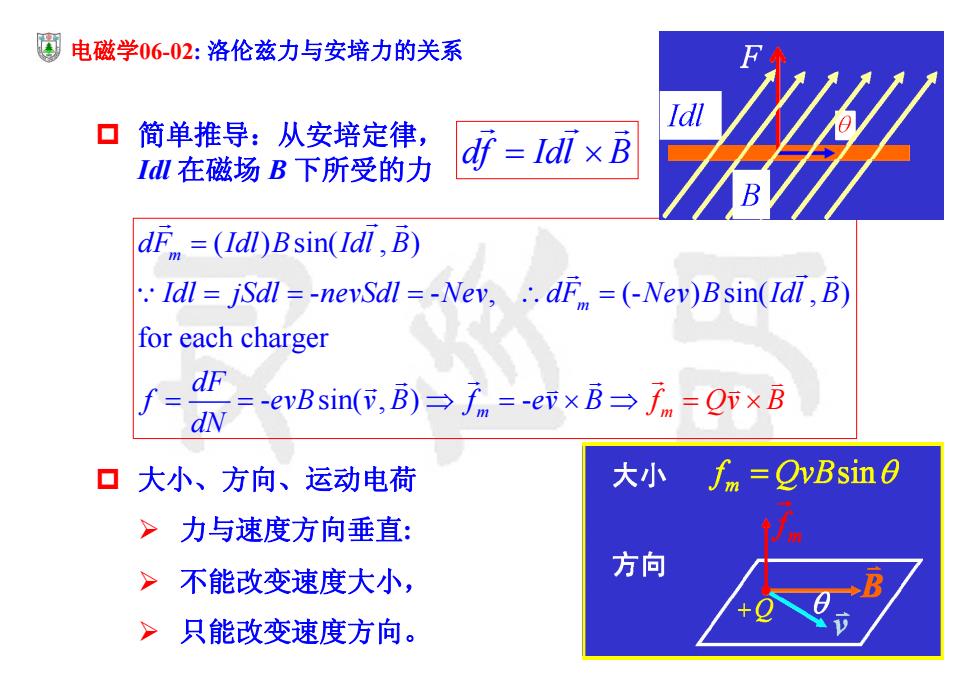
圜电磁学06-02:洛伦兹力与安培力的关系 口简单推导:从安培定律, Idl在磁场B下所受的力 df Idl x B dF =(Idl)Bsin(Idl,B) Idl jSdl =-nevSdl =-Nev,..dF =(-Nev)Bsin(Idl,B) for each charger dF dN =-evBsin(,B)→方m=-epxB→fm=O×B 口大小、方向、运动电荷 大小 =OvBsin >力与速度方向垂直: >不能改变速度大小, 方向 >只能改变速度方向
( ) sin( , ) - - , (- ) sin( , ) for each charger - sin( , ) - m m m m dF Idl B Idl B Idl jSdl nevSdl Nev dF Nev B Idl B dF f evB v B f eB f Qv dN v B 电磁学06-02: 洛伦兹力与安培力的关系 简单推导:从安培定律, Idl 在磁场 B 下所受的力 大小、方向、运动电荷 力与速度方向垂直: 不能改变速度大小, 只能改变速度方向。 df Idl B
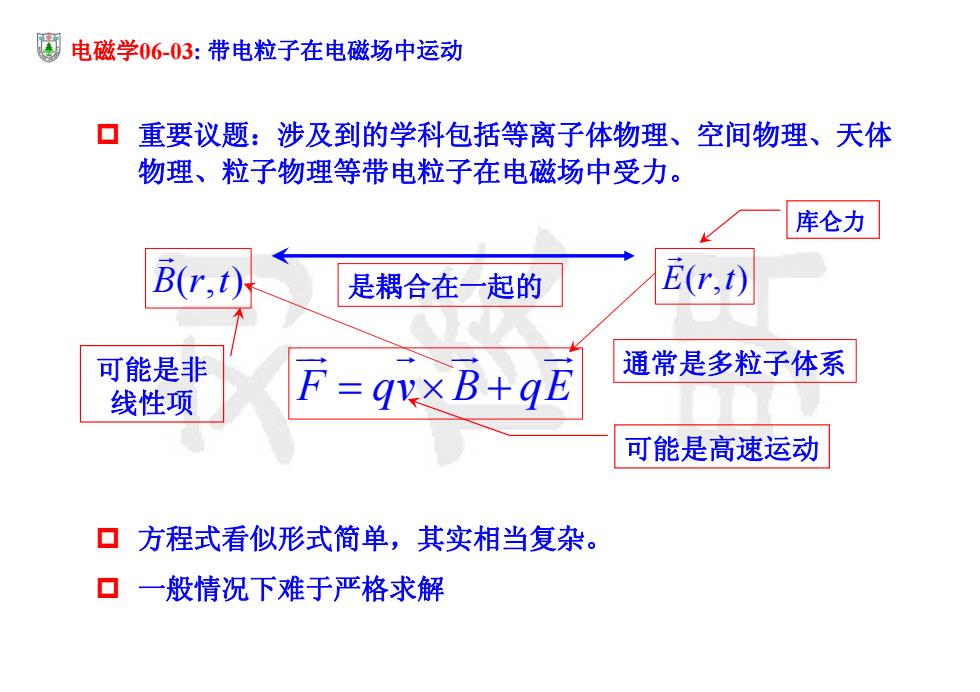
圆电磁学06-03:带电粒子在电磁场中运动 ▣重要议题:涉及到的学科包括等离子体物理、空间物理、天体 物理、粒子物理等带电粒子在电磁场中受力。 库仑力 B(r,t) 是耦合在一起的 E(r,t) 可能是非 通常是多粒子体系 线性项 F=quxB+gE 可能是高速运动 ▣方程式看似形式简单,其实相当复杂。 ▣一般情况下难于严格求解
电磁学06-03: 带电粒子在电磁场中运动 重要议题:涉及到的学科包括等离子体物理、空间物理、天体 物理、粒子物理等带电粒子在电磁场中受力。 方程式看似形式简单,其实相当复杂。 一般情况下难于严格求解 F qv B qE E(,) r t 库仑力 B(,) r t 是耦合在一起的 可能是非 线性项 通常是多粒子体系 可能是高速运动

圜电磁学06-03:带电粒子在电磁场中运动 ▣电磁场耦合情况下的近似: >如果外场很强,感应场很弱,近似处理—感应场略 如果带电粒子稀薄,各个粒子的运动相互独立、彼此无关而又类似,则 可简化为讨论单个带电粒子在给定的外加电磁场中的运动。 ▣xB中B是非线性项,近似处理: >在磁场B随时空变化的情形下,需要在一定条件下使之线性化,才能求 得解析解: 如果磁场随时空的变化十分缓慢且无电场,则可将磁场的非均匀和非恒 定部分作为均匀、恒定磁场的小扰动来处理,把均匀恒定解作为零阶解 代入方程,使之线性化,再求出一阶解,并考察解的自洽性,这就是线 性化的一阶近似理论。 >书上讲到的大多数是简单的情形
电磁学06-03: 带电粒子在电磁场中运动 电磁场耦合情况下的近似: 如果外场很强,感应场很弱,近似处理——感应场略 如果带电粒子稀薄,各个粒子的运动相互独立、彼此无关而又类似,则 可简化为讨论单个带电粒子在给定的外加电磁场中的运动。 qvB 中 B 是非线性项,近似处理: 在磁场 B 随时空变化的情形下,需要在一定条件下使之线性化,才能求 得解析解; 如果磁场随时空的变化十分缓慢且无电场,则可将磁场的非均匀和非恒 定部分作为均匀、恒定磁场的小扰动来处理,把均匀恒定解作为零阶解 代入方程,使之线性化,再求出一阶解,并考察解的自洽性,这就是线 性化的一阶近似理论。 书上讲到的大多数是简单的情形
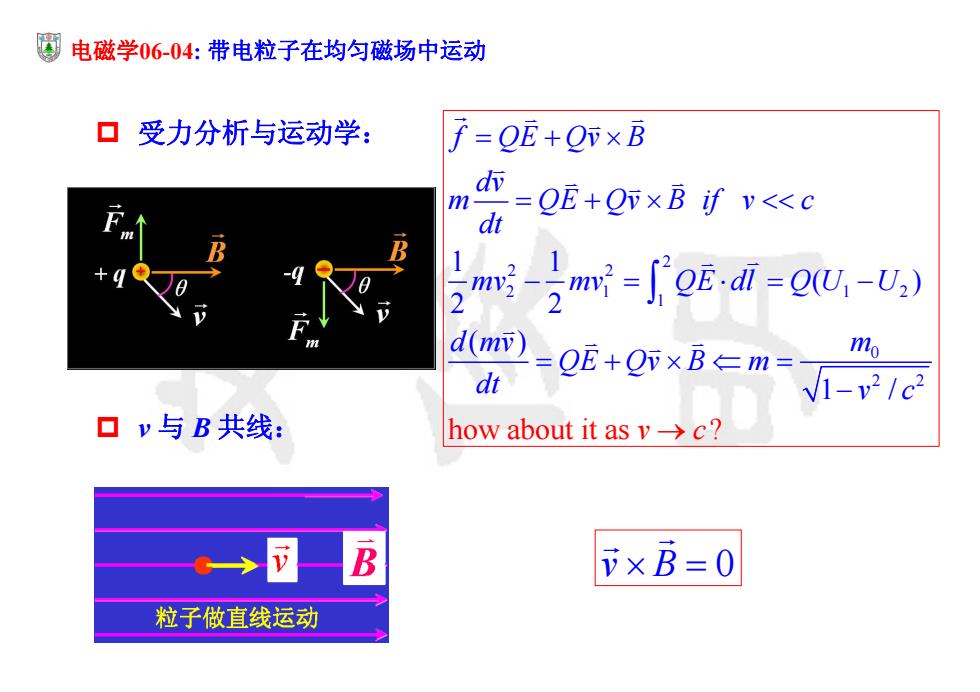
电磁学06-04:带电粒子在均匀磁场中运动 口受力分析与运动学: f=QE+Q下×B dv m =QE+Q×Bfvc? 。→同 B F×B=0 粒子做直线运动
电磁学06-04: 带电粒子在均匀磁场中运动 受力分析与运动学: 2 2 2 2 1 12 1 0 2 2 how about it 1 1 ( ) 2 2 ( a 1 ? / s ) f QE Qv B dv m QE Qv B if v c dt mv mv QE dl Q U U d mv m QE Qv B m dt v v c c v 与 B 共线: v B 0