
閻 第二章导体周围的静电场,静电能量
第二章 导体周围的静电场,静电能量

圆电磁学02-01:导体 口导体的性质: 口第一类导体(金属,均匀) O,=constant 口电平衡弛豫时间极短(瞬时) system 口周围不存在电介质,绝缘材 E=∑E=J∬r)d" 料的相对介电常数为1, 0=∑u,=j∬uoaw 口电荷密度、静止等定义均指 宏观量。 重,Bs=∑0>dE=-vU= £0S呐 60 口静电平衡条件: ∮E·dl=0→oE=0 口均匀导体内部场强处处为零 dE=0 (inside conductor) 口每个均匀导体都是等势体; 口电荷静止不动(宏观)
电磁学02-01: 导体 导体的性质: 第一类导体(金属,均匀) 电平衡弛豫时间极短(瞬时) 周围不存在电介质,绝缘材 料的相对介电常数为1, 电荷密度、静止等定义均指 宏观量。 静电平衡条件: 均匀导体內部场强处处为零 每个均匀导体都是等势体; 电荷静止不动(宏观)。 2 0 0 constant ( ) ( ) 1 0 0 0 (inside conductor) i i i system i Q V i Q V S S S Q E E E r dV U U U r dV E dS Q divE U E dl rotE dE 内
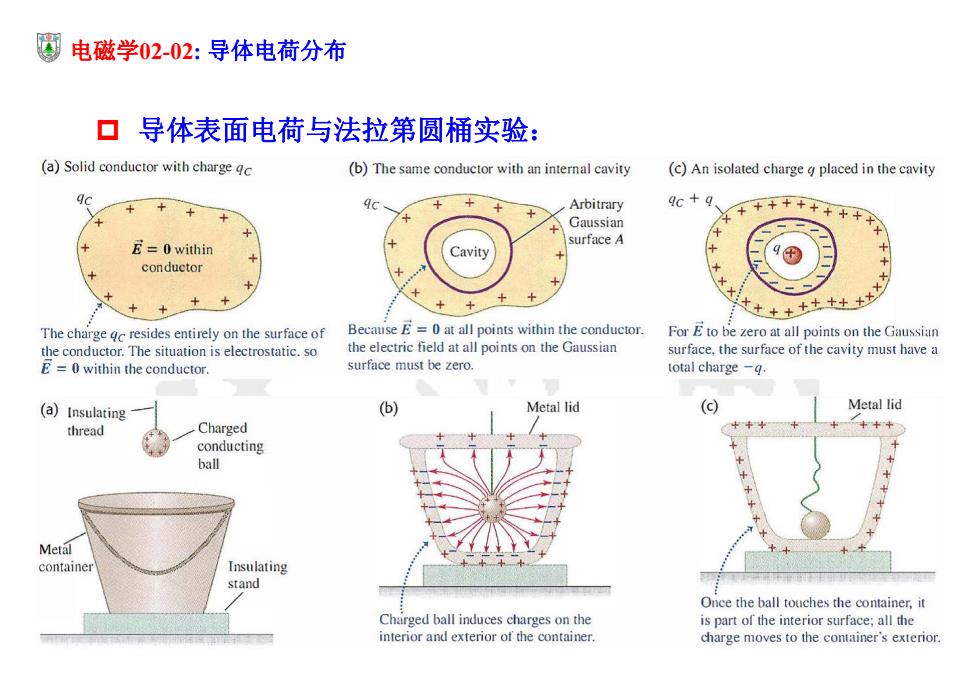
电磁学02-02:导体电荷分布 口导体表面电荷与法拉第圆桶实验: (a)Solid conductor with charge qc (b)The same conductor with an internal cavity (c)An isolated charge g placed in the cavity +十 + Arbitrary qc +q Gaussian =0 within surface A + Cavity + conductor + + The charge 4c resides entirely on the surface of Because E=0 at all points within the conductor. For Eto be zero at all points on the Gaussian the conductor.The situation is electrostatic.so the electric field at all points on the Gaussian surface,the surface of the cavity must have a E =0 within the conductor. surface must be zero. total charge -g. (a))Insulating (b) Metal lid () Metal lid thread Charged conducting ball Metal container Insulating stand Once the ball touches the container,it Charged ball induces charges on the is part of the interior surface;all the interior and exterior of the container. charge moves to the container's exterior
电磁学02-02: 导体电荷分布 导体表面电荷与法拉第圆桶实验:
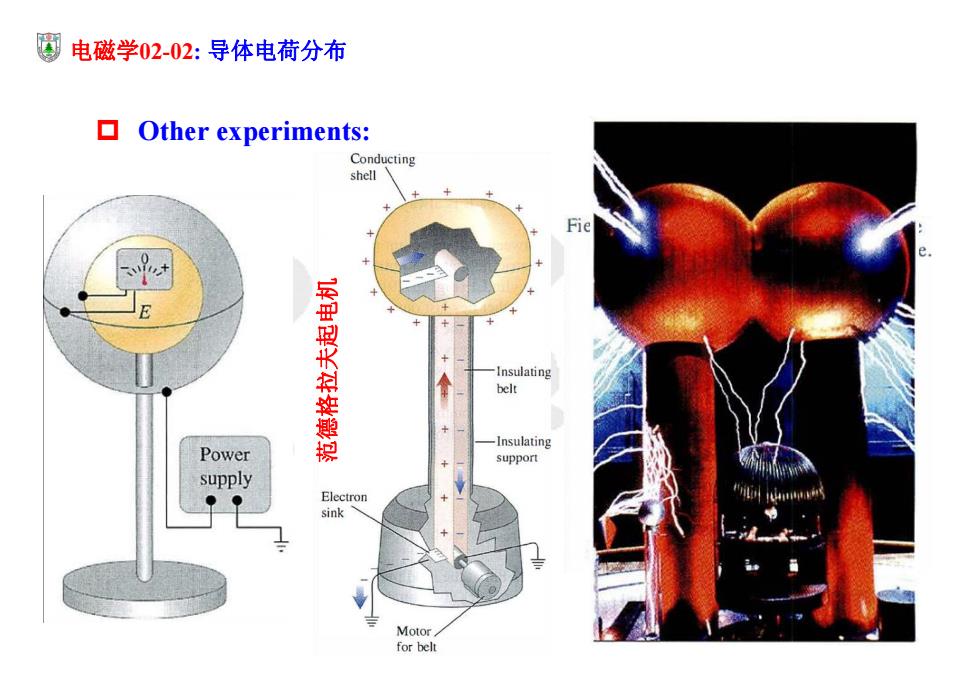
圆电磁学02-02:导体电荷分布 ▣Other experiments: Conducting shell Fie -Insulating belt -Insulating Power support supply Electron sink Motor for belt
电磁学02-02: 导体电荷分布 Other experiments: 范德格拉夫起电机
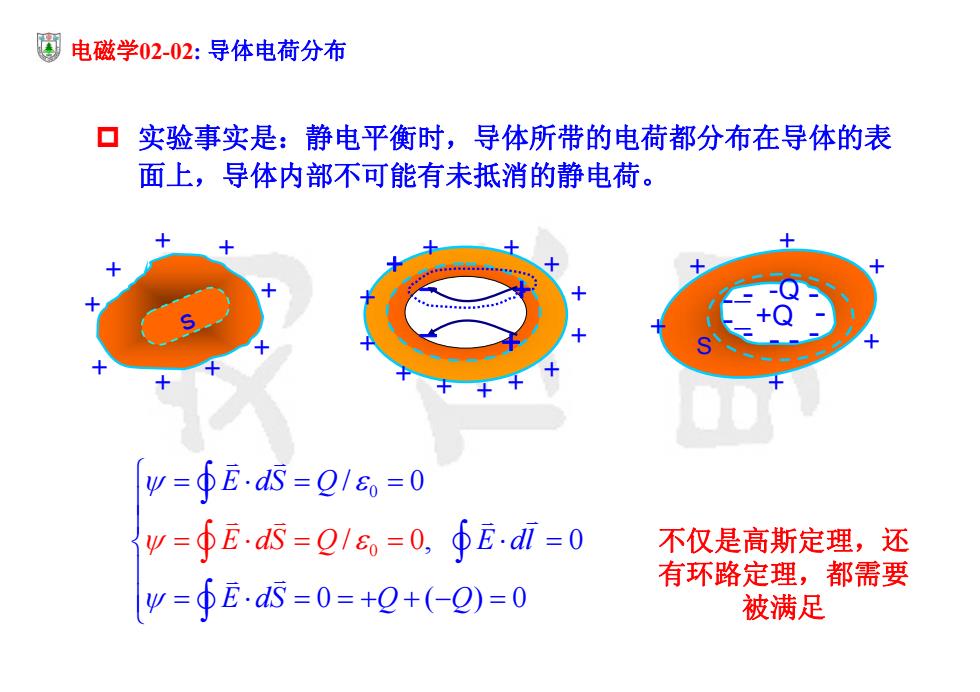
电磁学02-02:导体电荷分布 ▣实验事实是:静电平衡时,导体所带的电荷都分布在导体的表 面上,导体内部不可能有未抵消的静电荷。 w=∮E.d=0/6=0 w=∮Eds=0/6=0,fEdl=0 不仅是高斯定理,还 有环路定理,都需要 w=∮E.S=0=+9+(-2)=0 被满足
电磁学02-02: 导体电荷分布 实验事实是:静电平衡时,导体所带的电荷都分布在导体的表 面上,导体内部不可能有未抵消的静电荷。 + + + + + + + + + s + _ _ + + + + + +Q -Q S - - - - - - - - - 0 0 / 0 / 0, 0 0 ( )0 E dS Q E dl E dS E S Q d Q Q + + + + + + + + + + + + + - + - + 不仅是高斯定理,还 有环路定理,都需要 被满足

厦电磁学02-02:导体电荷分布 口【例2.1.7】一导体球壳A带有电荷量q4<0,导体小球B带有电 荷量q0。用绝缘丝带吊起小球B经小孔放入球壳A内。 ()B与A不接触,另A瞬时接地,然后断开接地,将B取出。球壳 A与小球B带电情况如何? (2)B与A的内壁接触,A不接地,然后将B取出。球壳A与小球B 带电情况如何? 静电平衡条件下上面的球 壳内表面有电荷么?
电磁学02-02: 导体电荷分布 【例2.1.7】一导体球壳 A 带有电荷量 qA0。用绝缘丝带吊起小球B经小孔放入球壳A内。 (1) B与A不接触,另A瞬时接地,然后断开接地,将B取出。球壳 A与小球B带电情况如何? (2) B与A的内壁接触,A不接地,然后将B取出。球壳A与小球B 带电情况如何? 静电平衡条件下上面的球 壳内表面有电荷么?
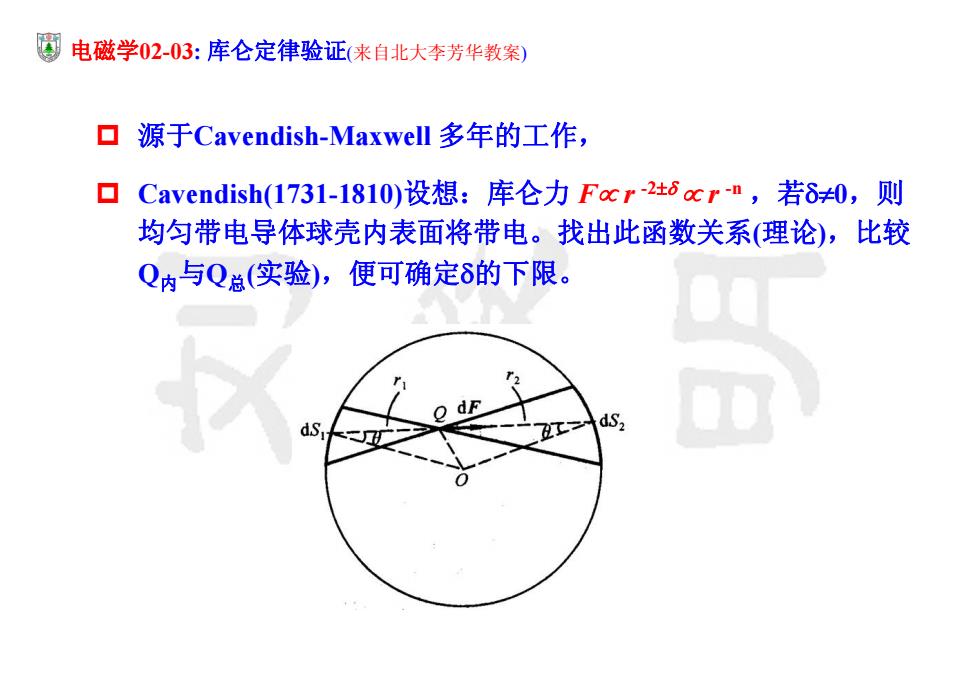
电磁学02-03:库仑定律验证(来自北大李芳华教案) 口源于Cavendish-Maxwell多年的工作, ▣Cavendish(1731-1810)设想:库仑力Facr-2t6cr-",,若δ≠0,则 均匀带电导体球壳内表面将带电。找出此函数关系(理论),比较 Q内与Q总(实验),便可确定δ的下限。 o d ds ds
电磁学02-03: 库仑定律验证(来自北大李芳华教案) 源于Cavendish-Maxwell 多年的工作, Cavendish(1731-1810)设想:库仑力 F r -2 r -n ,若0,则 均匀带电导体球壳内表面将带电。找出此函数关系(理论),比较 Q内与Q总(实验),便可确定的下限
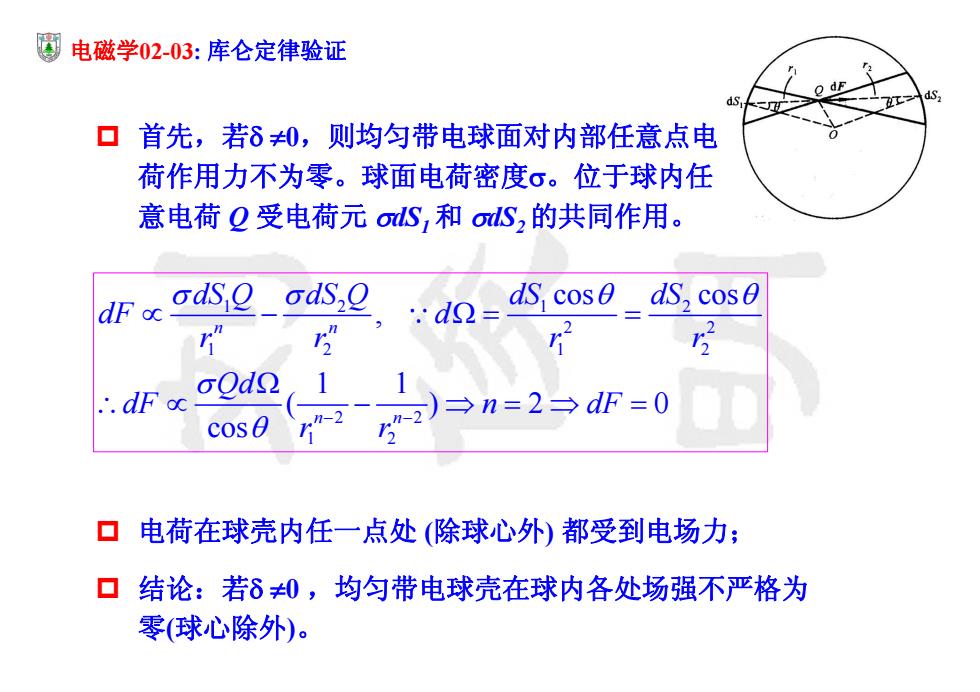
厦电磁学02-03:库仑定律验证 口首先,若δ0,则均匀带电球面对内部任意点电 荷作用力不为零。球面电荷密度σ。位于球内任 意电荷Q受电荷元olS,和olS,的共同作用。 odS2σdS, ,·dQ=Scos0 ds,cos r ∴.dFoc oOdg cos0 n-2 g)→n=2→df=0 口电荷在球壳内任一点处(除球心外)都受到电场力; 口结论:若δ0,均匀带电球壳在球内各处场强不严格为 零(球心除外)
电磁学02-03: 库仑定律验证 首先,若 0,则均匀带电球面对内部任意点电 荷作用力不为零。球面电荷密度。位于球内任 意电荷 Q 受电荷元 dS1 和 dS2 的共同作用。 12 1 2 2 2 12 1 2 2 2 1 2 cos cos , 1 1 ( )2 0 cos n n n n dS Q dS Q dS dS dF d rr r r Qd dF n dF r r 电荷在球壳内任一点处 (除球心外) 都受到电场力; 结论:若 0 ,均匀带电球壳在球内各处场强不严格为 零(球心除外)
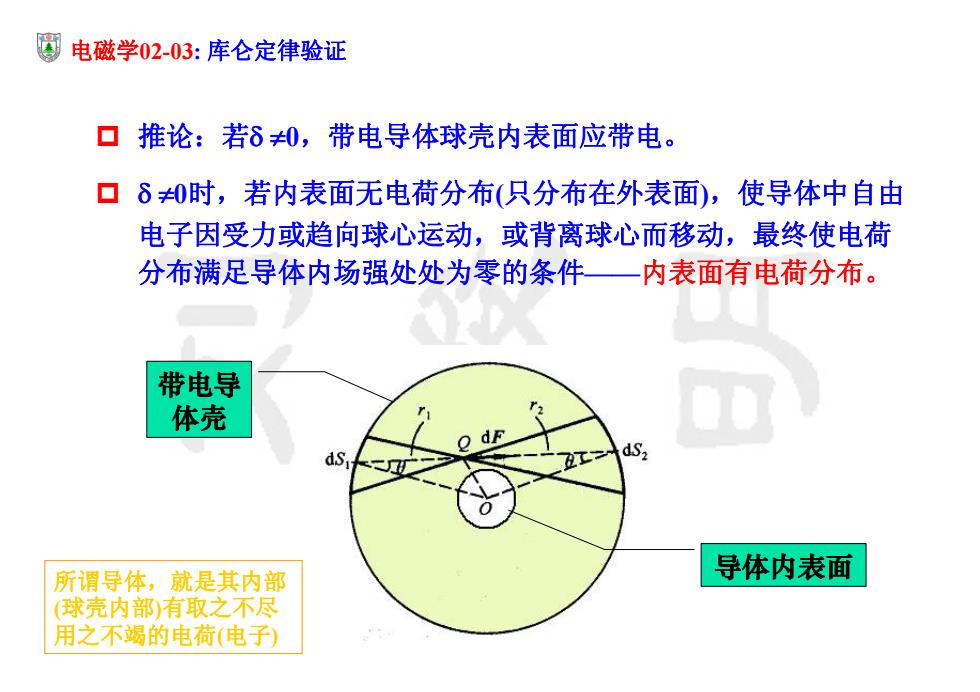
电磁学02-03:库仑定律验证 口推论:若δ0,带电导体球壳内表面应带电。 ▣δ0时,若内表面无电荷分布(只分布在外表面),使导体中自由 电子因受力或趋向球心运动,或背离球心而移动,最终使电荷 分布满足导体内场强处处为零的条件一内表面有电荷分布。 带电导 体壳 ds. 所谓导体,就是其内部 导体内表面 球壳内部)有取之不尽 用之不竭的电荷(电子)
电磁学02-03: 库仑定律验证 推论:若 0,带电导体球壳内表面应带电。 0时,若内表面无电荷分布(只分布在外表面),使导体中自由 电子因受力或趋向球心运动,或背离球心而移动,最终使电荷 分布满足导体内场强处处为零的条件——内表面有电荷分布。 导体内表面 带电导 体壳 所谓导体,就是其内部 (球壳内部)有取之不尽 用之不竭的电荷(电子)

圆电磁学02-03:库仑定律验证 口1773年:“我取一个直径为12.1英寸的球 ,用一根实心的玻璃棒穿过中心当作轴 并覆盖以封蜡。...然后把这个球封 在两个中空的半球中间,半球直径为 13.3英寸,120英寸厚。...然后,我 用一根导线将莱顿瓶的正极接到半球, 使半球带电。” 绝缘支柱 ▣用一根导线将内外球联在一起,外球壳 木髓球 验电器 带电后,取走导线,打开外球壳,用木 髓球验电器试验内球。 口木髓球验电器没有指示,证明内球没带 电,指数6≤0.02
电磁学02-03: 库仑定律验证 1773年:“我取一个直径为12.1英寸的球 ,用一根实心的玻璃棒穿过中心当作轴 ,并覆盖以封蜡。……然后把这个球封 在两个中空的半球中间,半球直径为 13.3英寸,1/20英寸厚。……然后,我 用一根导线将莱顿瓶的正极接到半球, 使半球带电。” 用一根导线将内外球联在一起,外球壳 带电后,取走导线,打开外球壳,用木 髓球验电器试验内球。 木髓球验电器没有指示,证明内球没带 电,指数0.02