
第11章静电场 §11.1静电学基本问题 §11.2电场电场强度 §11.3高斯定理及应用 §11.4环路定理与电势 §11.5电势与电场强度的关系 静电场部分习题课内容
第 11 章 静电场 §11.1 静电学基本问题 静电学基本问题 §11.2 电场 电场强度 §11.3 高斯定理及应用 高斯定理及应用 §11.4 环路定理与电势 环路定理与电势 §11.5 电势与电场强度的关系 电势与电场强度的关系 静电场部分习题课内容 静电场部分习题课内容
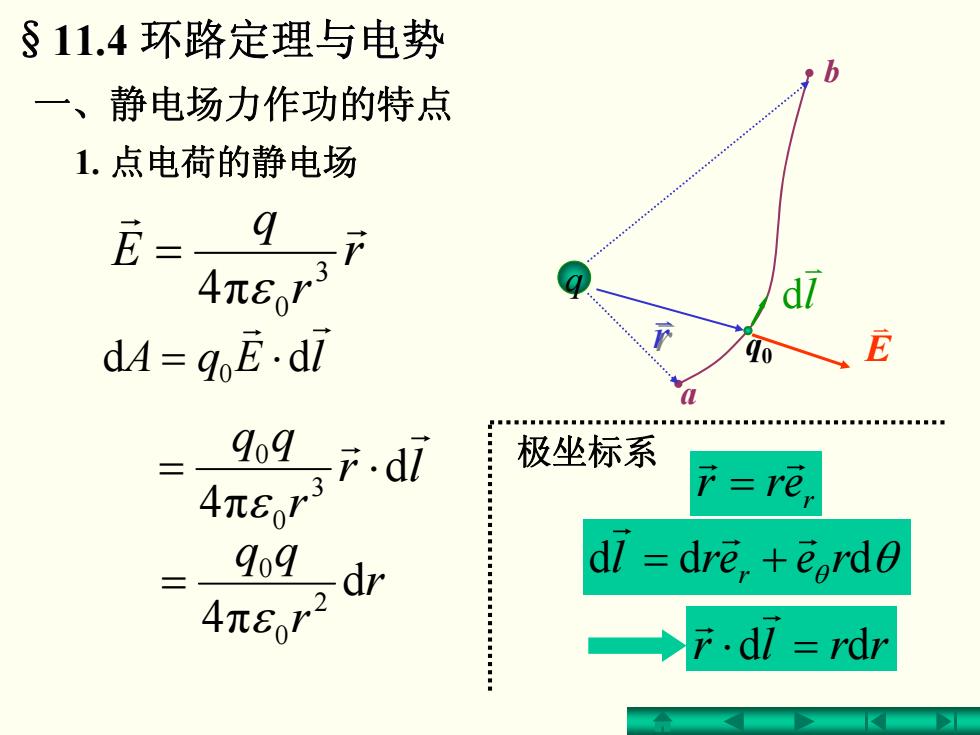
§11.4环路定理与电势 一、静电场力作功的特点 1.点电荷的静电场 E= q 4πe,1 dA=goE.dl 9o9 r.dl 极坐标系 4π8or =re, 9o9 、dr dl dre,eordo 4π8or1 →.di=rdr
§11.4 环路定理与电势 环路定理与电势 一、静电场力作功的特点 q q0 b a r v r v E v lEqA r r dd 0 ⋅= r r q E r r 3 π 0 4 ε = lr r qq r r d 4π 3 0 0 ⋅= ε 1. 点电荷的静电场 l v d r r qq d 4π 2 0 0 ε = r θreerl ddd θ r r r += 极坐标系 =⋅ dd rrlr r r r err r r =

94 11 4π6, dl 点电荷场力作功与具体路径无关! 2.一般电荷分布的静电场 L=心g.-di-a∑E)di-∑心aE)-d 因(qE,)d1与路径无关,则A与路径无关!
r r qq A b a r r ab d 4 π 2 0 0 ∫ = ε ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = − ba rr qq 11 4 π 0 0 ε 点电荷场力作功与具体路径无关! 2. 一般电荷分布的静电场 ∫ ⋅= b a ab 0 d)( lEqA ∫ ∑ ⋅= b a i 0 i d)( lEq ∑ ∫ = ⋅ i b a i lEq r r d)( 0 因 ∫ ⋅ 与路径无关,则 Aab与路径无关! b a i lEq r r d)( 0 q q 0 b a r v r v E v l v d
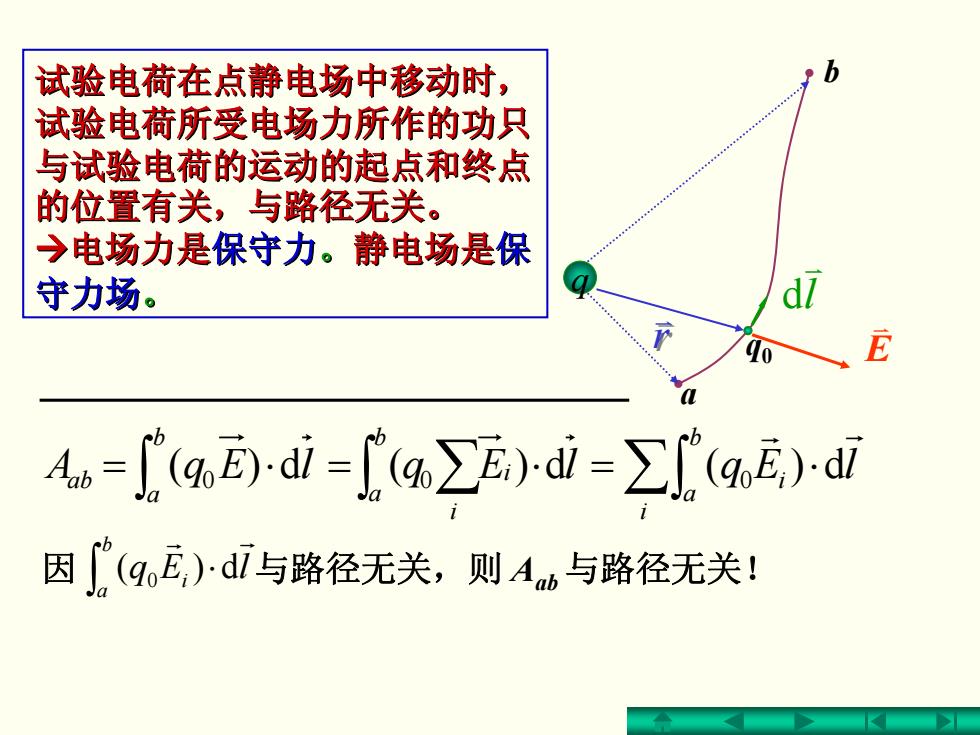
试验电荷在点静电场中移动时, 试验电荷所受电场力所作的功只 与试验电荷的运动的起点和终点 的位置有关,与路径无关。 →电场力是保守力。静电场是保 守力场。 d 人-心a-di-心a∑)-di=∑aE,)-d 因心(q,)di与路径无关,则A与路径无关!
∫ ⋅= ba ab 0 d)( lEqA ∫ ∑ ⋅= ba i 0 i d)( lEq ∑∫ = ⋅ i b a i lEq r r d)( 0 因 ∫ ⋅ 与路径无关,则 Aab与路径无关! ba i lEq r r d)( 0 q q0 b a r v r v E v l v d 试验电荷在点静电场中移动时, 试验电荷在点静电场中移动时, 试验电荷所受电场力所作的功只 试验电荷所受电场力所作的功只 与试验电荷的运动的起点和终点 与试验电荷的运动的起点和终点 的位置有关,与路径无关。 的位置有关,与路径无关。 Æ电场力是保守力。静电场是保 守力场
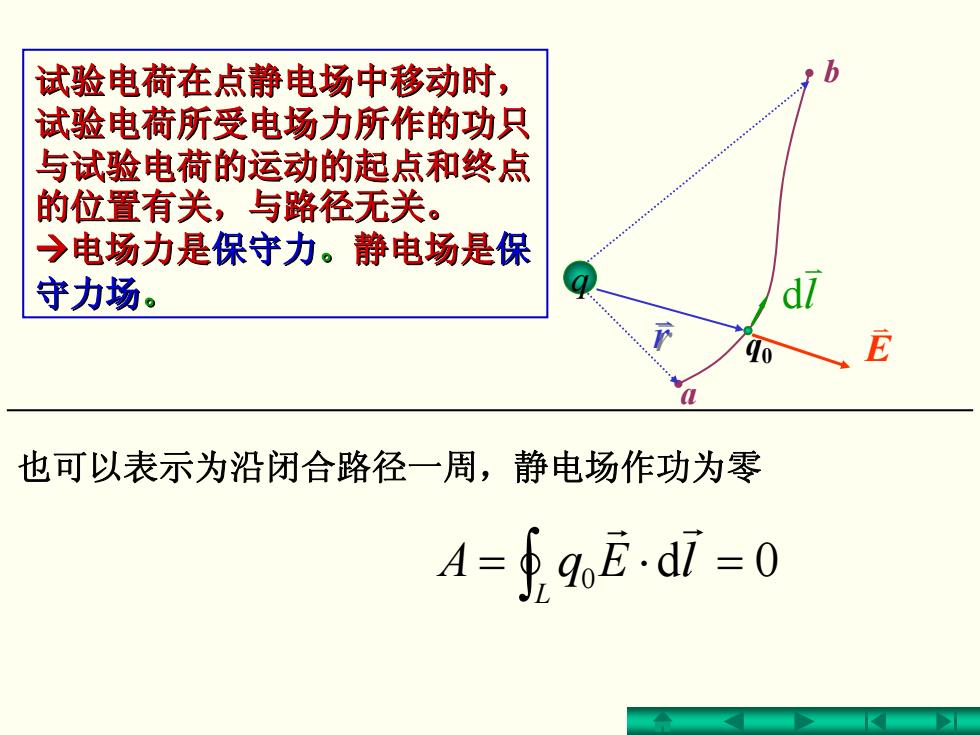
试验电荷在点静电场中移动时, 试验电荷所受电场力所作的功只 与试验电荷的运动的起点和终点 的位置有关,与路径无关。 →电场力是保守力。静电场是保 守力场。 0 也可以表示为沿闭合路径一周,静电场作功为零 4=q0E.d7=0
也可以表示为沿闭合路径一周,静电场作功为零 0 =⋅= 0d ∫L lEqA r r 试验电荷在点静电场中移动时, 试验电荷在点静电场中移动时, 试验电荷所受电场力所作的功只 试验电荷所受电场力所作的功只 与试验电荷的运动的起点和终点 与试验电荷的运动的起点和终点 的位置有关,与路径无关。 的位置有关,与路径无关。 Æ电场力是保守力 。静电场是 保 守力场 。 q q 0 b a r v r v E v l v d

二、静电场的环路定理 fEd7=0 E·d1一称为静电场电场强度沿闭合回路的环流。 静电场环路定理 A=f9E.d7=0
二、静电场的环路定理 =⋅ 0d ∫L lEr r ——静电场环路定理 0 =⋅= 0d ∫L lEqA r r ——称为静电场电场强度沿闭合回路的环流。 ∫ ⋅ L lEr r d

讨论 fE-di-0 •静电场为保守力场 •环路定理是静电场的基本方程 •环路定理的微分形式 V×E=0 >静电场为无旋(度)场 >静电场为有源场
=⋅ 0d ∫L lEr r •静电场为保守力场 E =×∇ 0 r ¾静电场为无旋(度)场 ¾静电场为有源场 •环路定理是静电场的基本方程 •环路定理的微分形式 讨论
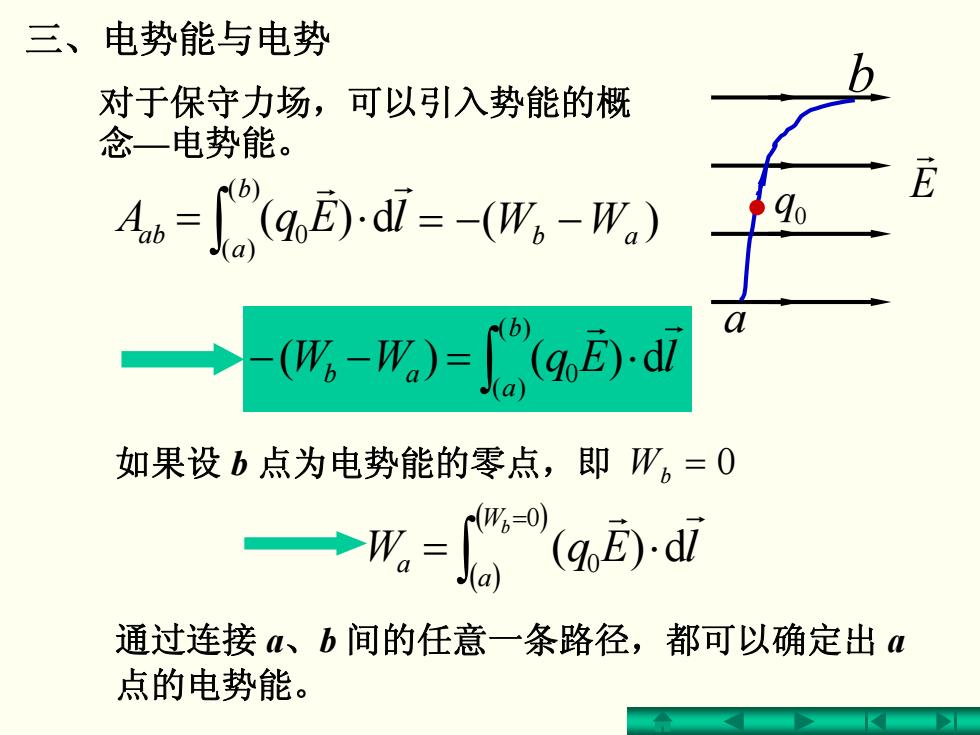
三、电势能与电势 对于保守力场,可以引入势能的概 念一电势能。 A=(g面-d=-(。-W) -(%-Wa)=O(g,-dl 如果设b点为电势能的零点,即W。=0 →形= (E).dl 通过连接、b间的任意一条路径,都可以确定出a 点的电势能
)( = − −WW ab 三、电势能与电势 ∫ ⋅=−− )( )( 0 d)()( ba ab lEqWW r r 对于保守力场,可以引入势能的概 念—电势能。 如果设 b 点为电势能的零点,即 Wb = 0 ( ) ( ) ∫ = = ⋅ 0 0 d)( Wb a a lEqW r r 通过连接 a、b 间的任意一条路径,都可以确定出 a 点的电势能。 ∫ ⋅= )( )( 0 d)( ba ab lEqA r r E r q0 a b

w,-%)=g,dl Ed- _W。 9o W 与试验电荷无关,只与电场在 9o a、b两点的性质有关。 W 可以引入一个新的物理量—电势V= 90
⎟⎟⎠⎞ ⎜⎜⎝⎛ −−=⋅ ∫ 00 )( )( d qW qW lE ab ba r r ⎟⎟⎠⎞ ⎜⎜⎝⎛ −− 00 qW qW ab ——与试验电荷无关,只与电场在 a、b两点的性质有关。 ∫ ⋅=−− )( )( 0 d)()( ba ab lEqWW r r 可以引入一个新的物理量——电势 q0 W V =

E. i- W_ W (a) 9o 9o W V= 90 8E.i=心-g) 一称a、b两点间电势差 若选b点的电势为参考零点,则点的电势为: (电势零点) E.dl
( ) ( ) ∫ ⋅ ba lEr r d ( ) ∫ ⋅= )( d 电势零点 a a lEV r r 若选 b 点的电势为参考零点,则 a 点的电势为: )( = − −VV ab —称 a、b 两点间电势差 q0 W V = ⎟⎟⎠⎞ ⎜⎜⎝⎛ −−=⋅ ∫ 00 )( )( d qW qW lE ab ba r r