
第11章静电场 §11.1静电学基本问题 §11.2电场电场强度 §11.3高斯定理及应用 §11.4环路定理与电势 §11.5电势与电场强度的关系 静电场部分习题果内容
第 11 章 静电场 §11.1 静电学基本问题 静电学基本问题 §11.2 电场 电场强度 §11.3 高斯定理及应用 高斯定理及应用 §11.4 环路定理与电势 环路定理与电势 §11.5 电势与电场强度的关系 电势与电场强度的关系 静电场部分习题课内容 静电场部分习题课内容
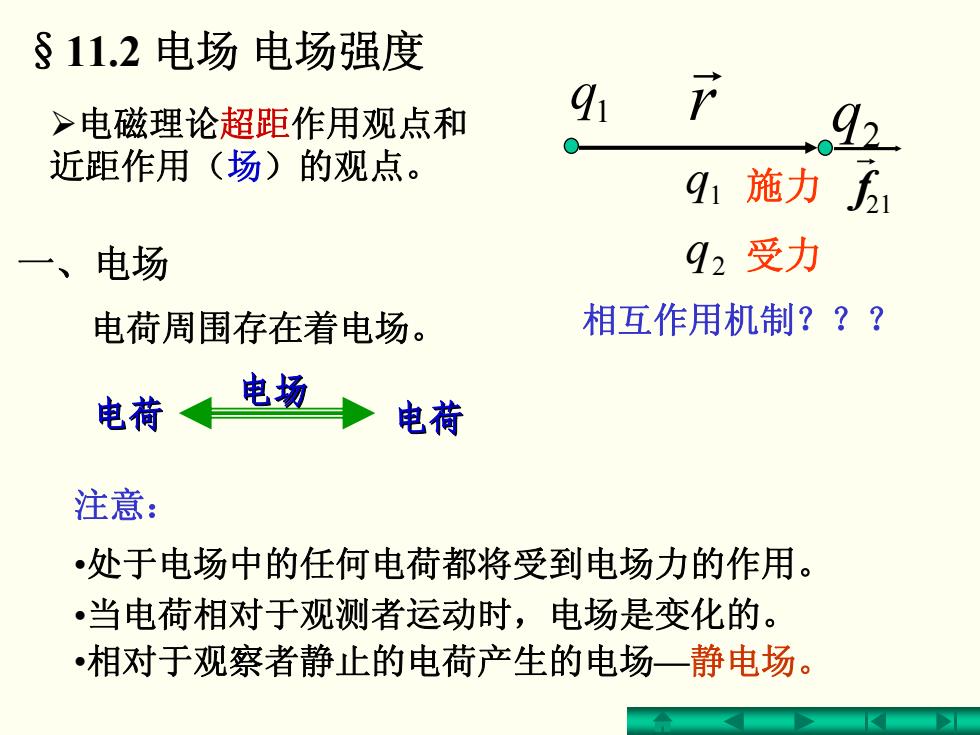
§11.2电场电场强度 >电磁理论超距作用观点和 91产 92 近距作用(场)的观点。 91施力 一、电场 92受力 电荷周围存在着电场。 相互作用机制??? 电荷 电场 电荷 注意: •处于电场中的任何电荷都将受到电场力的作用。 •当电荷相对于观测者运动时,电场是变化的。 •相对于观察者静止的电荷产生的电场一静电场
§11.2 电场 电场强度 ¾电磁理论超距作用观点和 近距作用(场)的观点。 一、电场 q1 q2 r r 施力 2 受力 1 q q 21 f r 相互作用机制??? 电荷 电场 电荷 •处于电场中的任何电荷都将受到电场力的作用。 •相对于观察者静止的电荷产生的电场—静电场。 •当电荷相对于观测者运动时,电场是变化的。 电荷周围存在着电场。 注意:

二、电场强度 描述场中各点电场的强弱变化的物理量一电场强度。 试验电 (1)(正)点电荷一可以准确的测量电场的分布 荷条件 (2)电量足够小一不显著地影响电场的分布 把试验电荷放到电场中 (1)受力与位置(场点)有关 任意场点,测量受力情 况,试验表明: (2)比值 与试验电 荷无关 96 定义电场强度: 龙= 90 >电场强度的方向为正电荷所受电场力的方向
0 q f E r r = 试验电 荷条件 (1)(正)点电荷—可以准确的测量电场的分布 把试验电荷放到电场中 任意场点,测量受力情 况,试验表明: 定义电场强度: 与试验电 荷无关 二、电场强度 描述场中各点电场的强弱变化的物理量— 电场强度。 q0 f r (2)比值 (1)受力与位置(场点)有关 (2)电量足够小—不显著地影响电场的分布 ¾电场强度的方向为正电荷所受电场力的方向

讨论 ·静电场为矢量场:E=E(x,y,z) •电场强度单位:国际单位制 N.C-或:V.ml •定义电场强度后,点电荷()处于外电场中时 受电场作用力: J=gE
讨论 •静电场为矢量场: = zyxEE ),,( 国际单位制 -1 ⋅CN -1 或: ⋅mV •定义电场强度后,点电荷(q)处于外电场中时 受电场作用力: Eqf r r = •电场强度单位:

三、电场强度的叠加原理 1.点电荷的场强 根据库仑定律和场强的定义 >球对称 E(x,y,2=E(r) E(r)=const
三、电场强度的叠加原理 1. 点电荷的场强 q r e r Qq f r r 2 π 0 4 ε = r r E f q = r e r Q E r r 2 4 π 0 ε = ¾ 球对称 Q r e r r r 根据库仑定律和场强的定义 = rEzyxE )(),,( )( =cons t =cr rE
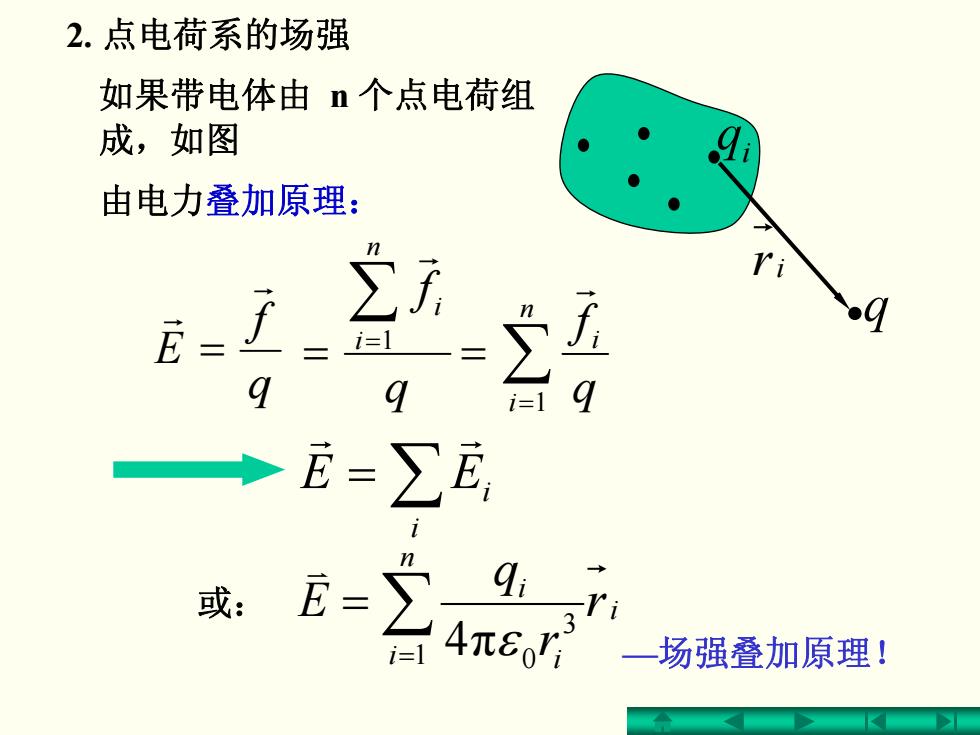
2.点电荷系的场强 如果带电体由n个点电荷组 成,如图 由电力叠加原理: B-I ∑ -i= +龙=∑E 或: - -r 4π8or 一场强叠加原理!
2. 点电荷系的场强 q f E r r = ∑ = = n i i q f 1 r = ∑ i EE i r r 如果带电体由 n 个点电荷组 成,如图 i q q 或: i n i i i r r q E ∑ = = 1 3 π 0 4 ε v q f n i ∑ i = = 1 r —场强叠加原理! 由电力叠加原理: ri
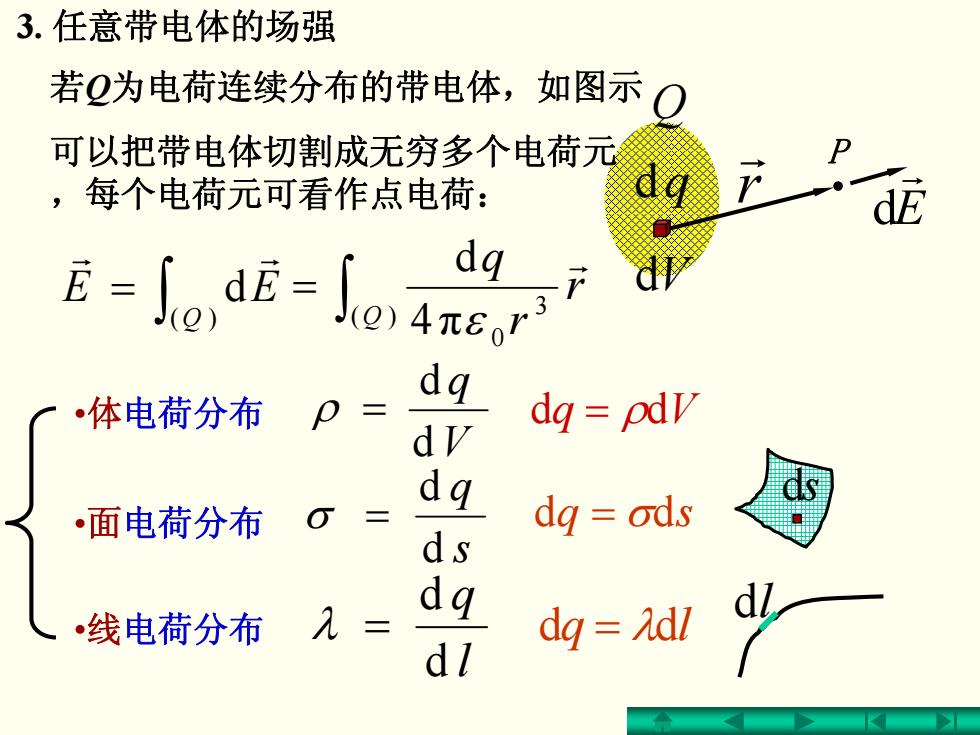
3.任意带电体的场强 若Q为电荷连续分布的带电体,如图示 可以把带电体切割成无穷多个电荷元 ,每个电荷元可看作点电荷: i-dE-lna盟7 dq dq •体电荷分布 dg=pdv dV dq ·面电荷分布 dg ods ds dq 线电荷分布 dq Adl dl
∫ = )( d Q EEr r E r d 若 Q为电荷连续分布的带电体,如图示 Q d q 可以把带电体切割成无穷多个电荷元 ,每个电荷元可看作点电荷: P r r • 体电荷分布 V q d d ρ = s q d d σ = l q d d λ = d V ds d l 3. 任意带电体的场强 • 面电荷分布 • 线电荷分布 ∫ = )( 3 4 π 0 d Q r r q r ε = ρdd Vq = σdd sq = λdd lq

[例11-1)求无限长均匀带电直线的电场分布。 解:在坐标y处取一个电荷元dq 电荷线密度为入 dq Ady dy -ln42 1 (xi-yj) (x2+y2)3/2 r=xi-yj 器产 xi r=(x2+y2)2
= λdd yq x 解:在坐标 y 处取一个电荷元 d q 电荷线密度为 λ [ 例11-1] 求无限长均匀带电直线的电场分布。 o x y . P E r d ∫ = )( 3 4 π 0 d Q P r r q E r ε r dy y ∫ ∞+∞− + − = 2/322 0 )( )( 4 π d yx jyixy ε λ ∫ ∞+∞− + = 2/322 0 4 π )( d yx ixy ε λ −= jyixr 2/122 += yxr )(

-号 xi 电荷线密度为入 Axi 1 y 4π80x2(x2+y2)V2 -∞0 d 2元80X r=xi-y方 r=(x2+y2)1V2
∫ ∞+∞− + = 2/322 0 4 π )( d yx ixy E P ε λ ∞+ ∞− + = 2/1222 0 )( 1 4 π yx y x ix ε λ i x 2 π 0 ε λ = x 电荷线密度为 λ o x y . P E r d r dy y −= jyixr 2/122 += yxr )(

Ep= 2元80X 场分布有柱对称性 讨论 几 E(r)= 2π8r P (2)电场强度沿直线到P E 点的方向 E 几 2元8r (3)对有限长度带电直导线 若r<L 无限长带电线
无限长带电线 讨论 ( 1)场分布有柱对称性 r rE 2 π 0 )( ε λ = ( 2)电场强度沿直线到 P 点的方向 r r E 2 2 π 0 ε λ = i x E P 2 π 0 ε λ = E ( 3)对有限长度带电直导线 o r . P 若 << Lr L r . P