
國 第四章恒稳电流 高 静电学不高明但很有实用价值的应用!
第四章 恒稳电流 静电学不高明但很有实用价值的应用!

电磁学0401:电流的几个概念 口静电学的核心:库仑定律 >环路定理 >高斯定理 >导体是等势体 >极化强度极化电荷/极化电场 = d4:d4→i-月 1 dq元2 4π60 r店 z 4π6月 dA=dgE.dl→④,Edl=0 fE.s=∑g Eo S dE =0 conductor D=8E+P
电磁学04-01: 电流的几个概念 静电学的核心:库仑定律 环路定理 高斯定理 导体是等势体 极化强度/极化电荷/极化电场 1 2 12 1 3 12 2 0 12 0 0 3 0 12 1 4 1 4 0 1 0 L S S conductor F dq E r dq r dA dq E dl E dl E dS q dE D EP dq dq F r r
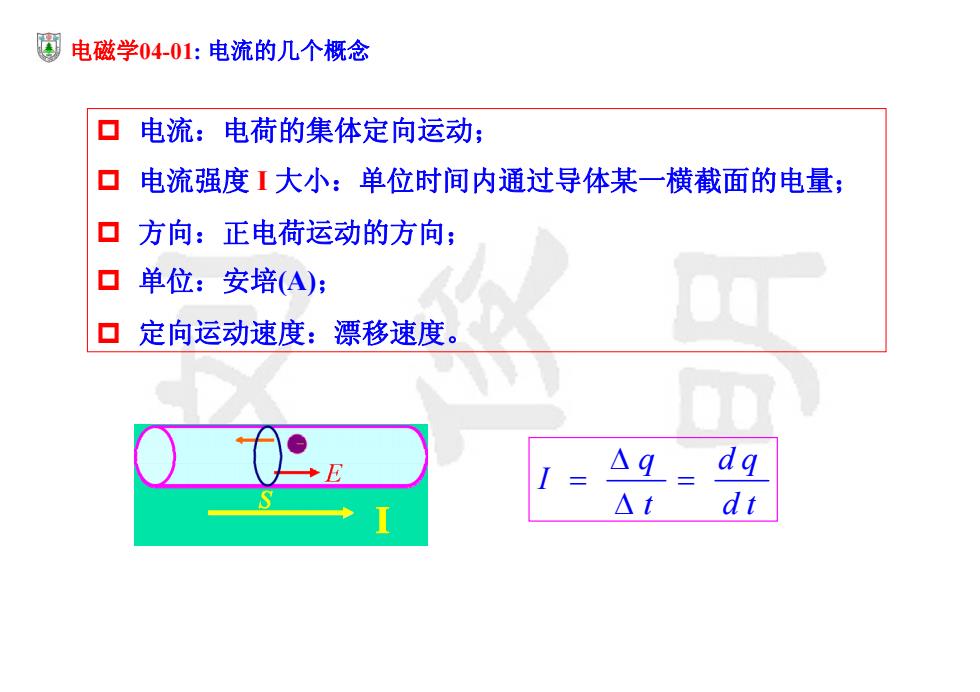
圈电磁学04-01:电流的几个概念 口电流:电荷的集体定向运动; 口电流强度I大小:单位时间内通过导体某一横截面的电量; 口方向:正电荷运动的方向; 口单位:安培(A) 口定向运动速度:漂移速度。 dq △t dt
电磁学04-01: 电流的几个概念 电流:电荷的集体定向运动; 电流强度 I 大小:单位时间内通过导体某一横截面的电量; 方向:正电荷运动的方向; 单位:安培(A); 定向运动速度:漂移速度。 q dq I t dt
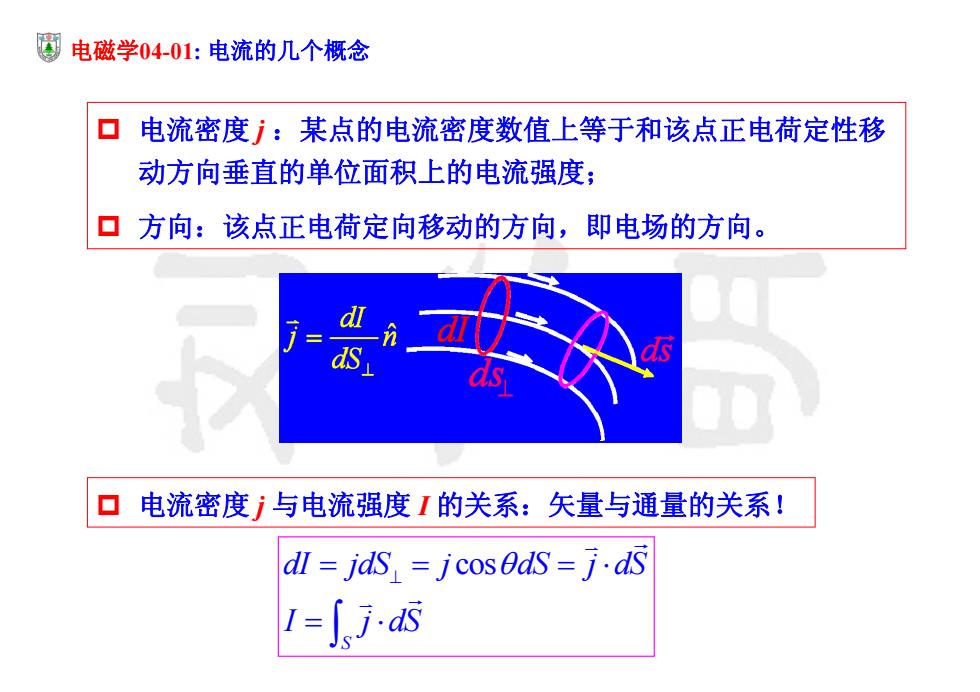
电磁学0401:电流的几个概念 ▣ 电流密度:某点的电流密度数值上等于和该点正电荷定性移 动方向垂直的单位面积上的电流强度; 口方向:该点正电荷定向移动的方向,即电场的方向。 口电流密度与电流强度1的关系:矢量与通量的关系! dl =jds jcosOds=j.ds 1=j
电磁学04-01: 电流的几个概念 电流密度 j :某点的电流密度数值上等于和该点正电荷定性移 动方向垂直的单位面积上的电流强度; 方向:该点正电荷定向移动的方向,即电场的方向。 电流密度 j 与电流强度 I 的关系:矢量与通量的关系! cos S dI jdS j dS j dS I j dS

电磁学04-01:电流的几个概念 ▣ 电流线:类比于电场线、电感应线; 口规定电流线上任一点的切线方向与该点的电流密度方向相同 。电流线的根数,则作以下规定:取一面元与电流线正交, 通过此面元的电流线的根数等于面元处的电流密度的大小与 该面元面积的乘积。电流线发出于正电荷减少的地方,终止 于正电荷增加的地方。 ▣ 电流线是虚构的,仅用来帮助我们设想电流密度的分布情况 ,建立物理图象
电磁学04-01: 电流的几个概念 电流线:类比于电场线、电感应线; 规定电流线上任一点的切线方向与该点的电流密度方向相同 。电流线的根数,则作以下规定:取一面元与电流线正交, 通过此面元的电流线的根数等于面元处的电流密度的大小与 该面元面积的乘积。电流线发出于正电荷减少的地方,终止 于正电荷增加的地方。 电流线是虚构的,仅用来帮助我们设想电流密度的分布情况 ,建立物理图象
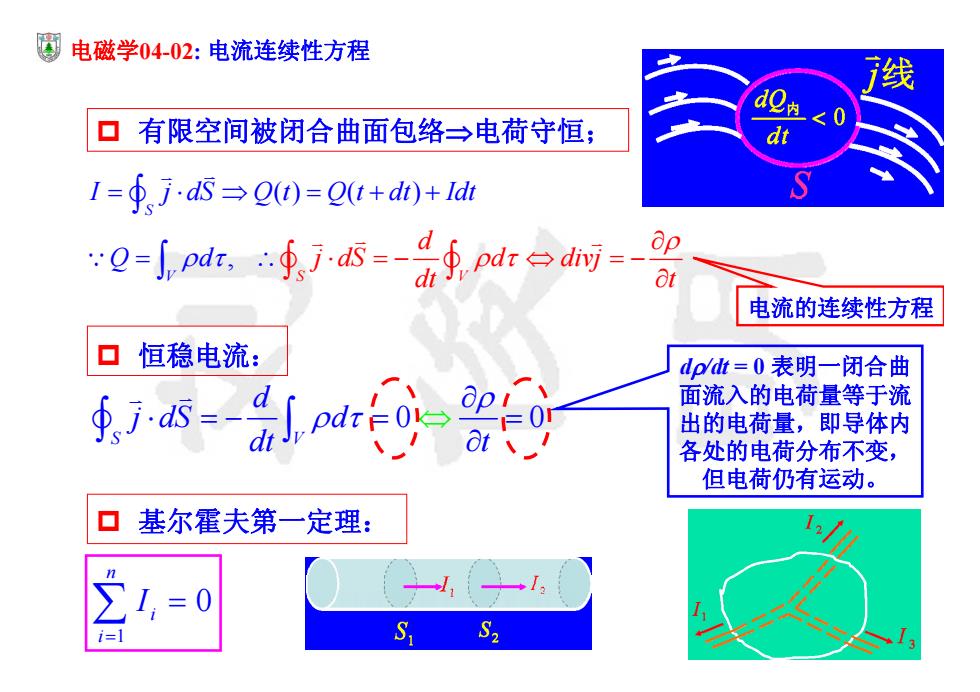
电磁学04-02:电流连续性方程 线 口有限空间被闭合曲面包络→电荷守恒; 1=∮,jS→Q0=0(t+d0+ld 0-Jpa,④,j=-4jdr台dmi=- 8t 电流的连续性方程 ▣ 恒稳电流: dp/t=0表明一闭合曲 面流入的电荷量等于流 出的电荷量,即导体内 各处的电荷分布不变, 但电荷仍有运动。 口基尔霍夫第一定理: i=
电磁学04-02: 电流连续性方程 有限空间被闭合曲面包络电荷守恒; 恒稳电流: () ( ) , V S V S d j dS d div I j dS Q t Q t j dt dt Idt Q d t 电流的连续性方程 0 0 S V d j dS d dt t d/dt = 0 表明一闭合曲 面流入的电荷量等于流 出的电荷量,即导体内 各处的电荷分布不变, 但电荷仍有运动。 基尔霍夫第一定理: 1 0 n i i I

圈电磁学0403:恒温电流电场 对于稳恒电流电场,静电场的两个基本方程式仍然成立。但与 静电场的性质并不完全相同; 口对于稳恒电路,导体内存在电场,稳恒电场由不随时间改变的 电荷分布而产生,因此仍然可以看成是稳态的、准静态的: 口环路定理与高斯定理: ∮E-di=0 U,-U,=∫E,dn÷E=-U ∮,D.d=∑0。 ∮Eas=∑(0,+Q)
电磁学04-03: 恒温电流电场 对于稳恒电流电场,静电场的两个基本方程式仍然成立。但与 静电场的性质并不完全相同; 对于稳恒电路,导体内存在电场,稳恒电场由不随时间改变的 电荷分布而产生,因此仍然可以看成是稳态的、准静态的; 环路定理与高斯定理: 1 2 1 0 2 0 0 1 ( ) 0 S S S S L D dS Q E dS Q E dl U U E dl E U Q 内 内

电磁学0403:恒温电流电场 静电场 稳恒电场 产生电场的电荷始终 电荷分布不随时间改变 固定不动 但伴随着电荷的定向移动 静电平衡时,导体内电 导体内电场不为零,导 场为零,导体是等势体 体内任意两点不是等势 电场有保守性,它是 电场有保守性,它是 保守场,或有势场 保守场,或有势场 维持静电场不需要 稳恒电场的存在总要 能量的转换 伴随着能量的转换
电磁学04-03: 恒温电流电场

电磁学0404:欧姆定律 ▣ 欧姆定律:I与U成正比 口电阻、电导的定义 U dU 1 I dl R= G= ▣电阻率p dl R元元 R-Ps-0-Vp p=AI+aT)台R=RI+adT) 线性电阻 非线性电阻 ▣欧姆定律的微分形式 ◆ ENI-AU-IR-JSR-jS(p)=jpAl E=pj台j=oE △
电磁学04-04: 欧姆定律 欧姆定律:I 与 U 成正比 电阻、电导的定义 电阻率 1 I U U dU I dI R G I dI R U dU 0 0 1 (1 ) (1 ) l R S T RR T 欧姆定律的微分形式 ( )l E l U IR jSR jS j l S EjjE
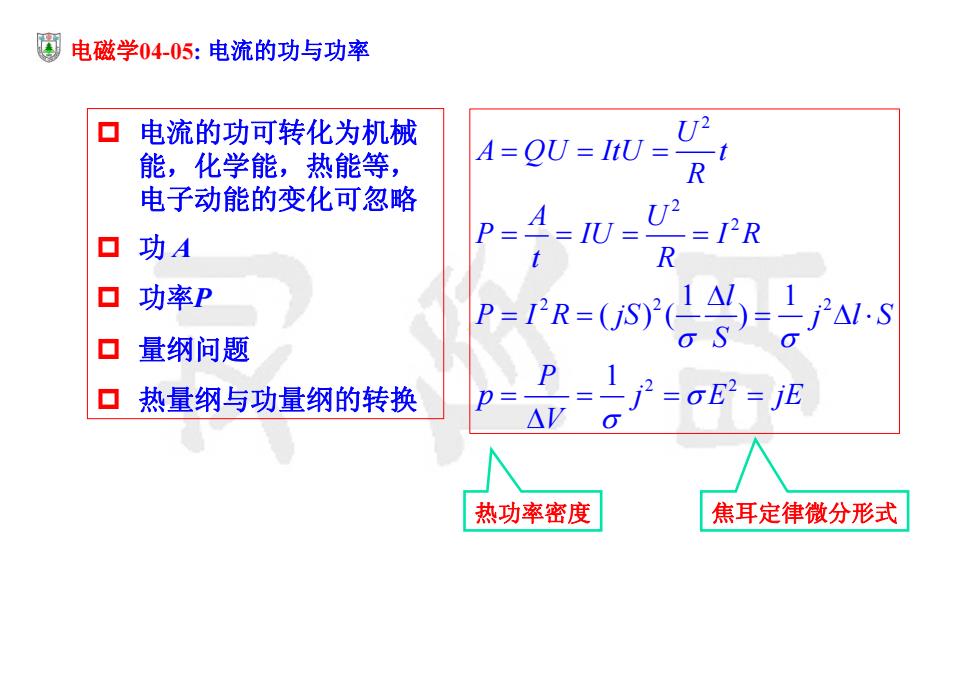
电磁学0405:电流的功与功率 ▣ 电流的功可转化为机械 U2 能,化学能,热能等, A=OU=ItU=- R 电子动能的变化可忽略 A U2 口功A P= == =I2R R 口功率P P=FR=(SY()=S ▣量纲问题 口热量纲与功量纲的转换 2=E2=jE 热功率密度 焦耳定律微分形式
电磁学04-05: 电流的功与功率 电流的功可转化为机械 能,化学能,热能等, 电子动能的变化可忽略 功 A 功率P 量纲问题 热量纲与功量纲的转换 2 2 2 22 2 2 2 1 1 ( )( ) 1 U A QU ItU t R A U P IU I R t R l P I R jS j l S S P p j E jE V 热功率密度 焦耳定律微分形式