
第13章电介质

第13章电介质 §13.1静电场中的电介质 §13.2介质中的高斯定理 §13.3介质边界两侧的静电场 §13.4静电场的能量
第 13 章 电介质 §13.2 介质中的高斯定理 介质中的高斯定理 §13.1 静电场中的电介质 静电场中的电介质 §13.4 静电场的能量 §13.3 介质边界两侧的静电场 介质边界两侧的静电场

§13.1静电场中的电介质 电介质: 除导体外的所有物质。 具有高电阻率的电介质—绝缘体。 电介质的特点: 原子中的电子被原子核束缚的很紧,不能自由 移动。介质内部没有可以自由移动的电荷。 在外电场中,物质分子中的正负电荷可以在分 子线度范围内移动—产生极化现象
除导体外的所有物质。 原子中的电子被原子核束缚的很紧,不能自由 移动。介质内部没有可以自由移动的电荷。 电介质的特点: 电介质: §13.1 静电场中的电介质 静电场中的电介质 具有高电阻率的电介质——绝缘体 。 在外电场中,物质分子中的正负电荷可以在分 子线度范围内移动——产生极化现象
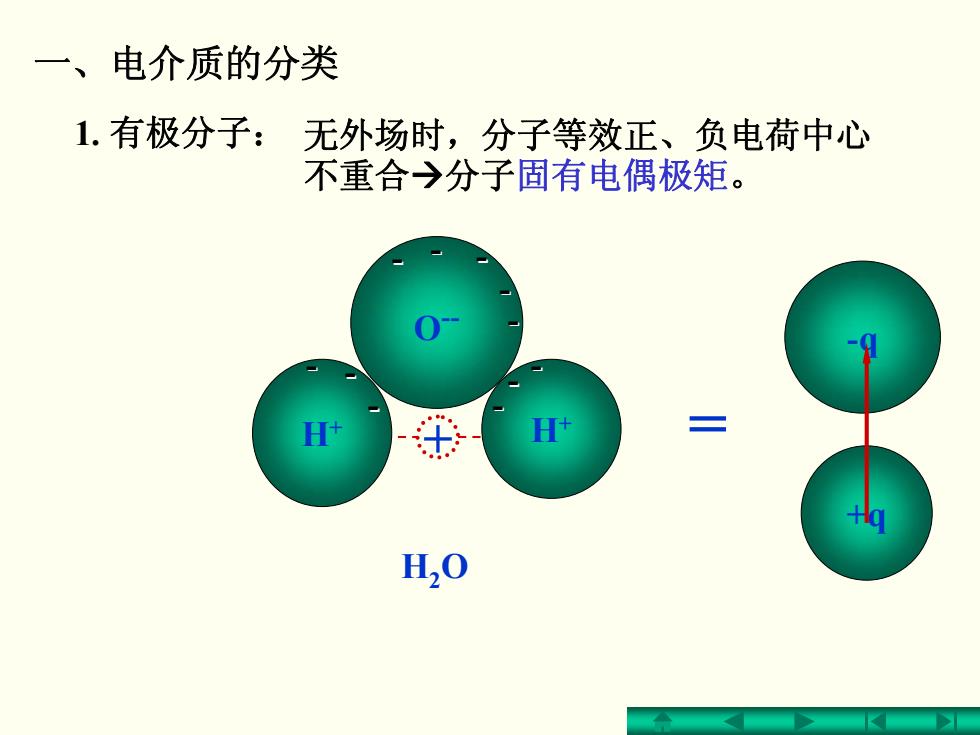
一、电介质的分类 1.有极分子:无外场时,分子等效正、负电荷中心 不重合→分子固有电偶极矩。 三 H20
一、电介质的分类 无外场时,分子等效正、负电荷中心 不重合Æ分子固有电偶极矩。 1. 有极分子: + -q +q = - O-- H+ H+ H2O - - - - - - - - - - -
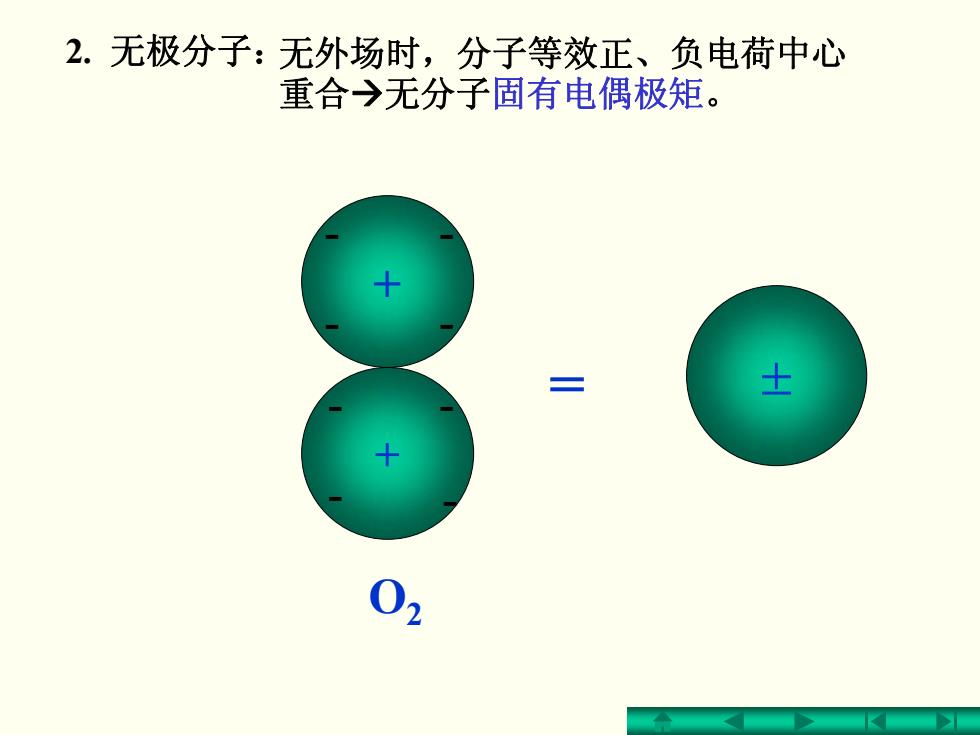
2.无极分子:无外场时,分子等效正、负电荷中心 重合→无分子固有电偶极矩。 士 02
无外场时,分子等效正、负电荷中心 重合 Æ无分子固有电偶极矩 。 2. 无极分子: = ± O 2 + + - - - - - - - -
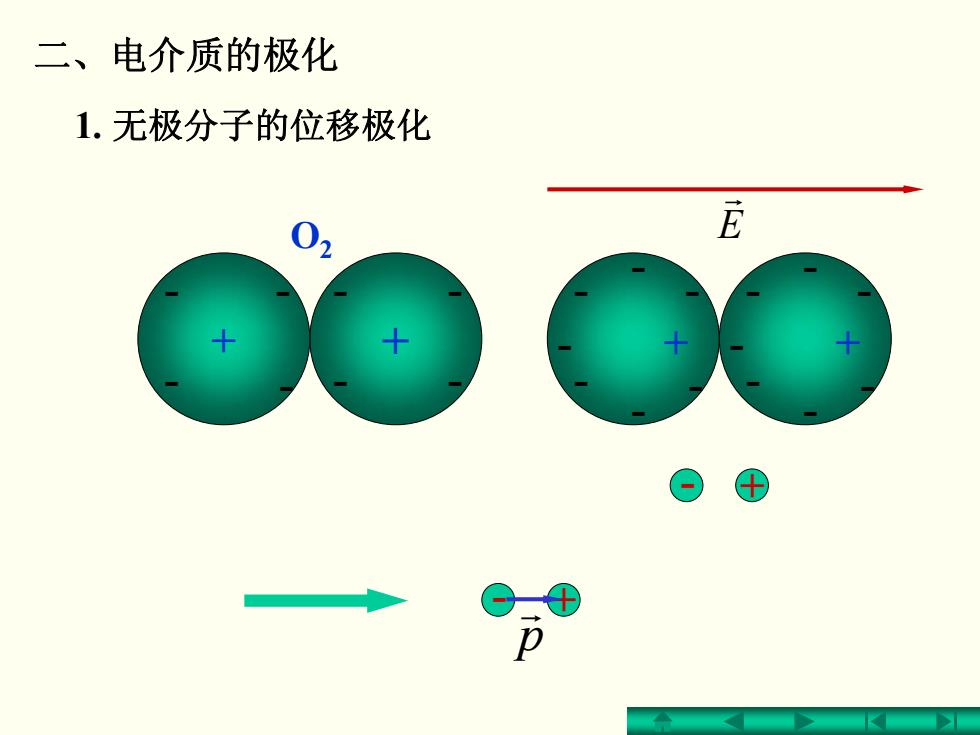
二、电介质的极化 1.无极分子的位移极化 E
O2 + + - - - - - - - - - - - - + - - - - - - - + - - - E r - + p r - + 1. 无极分子的位移极化 二、电介质的极化
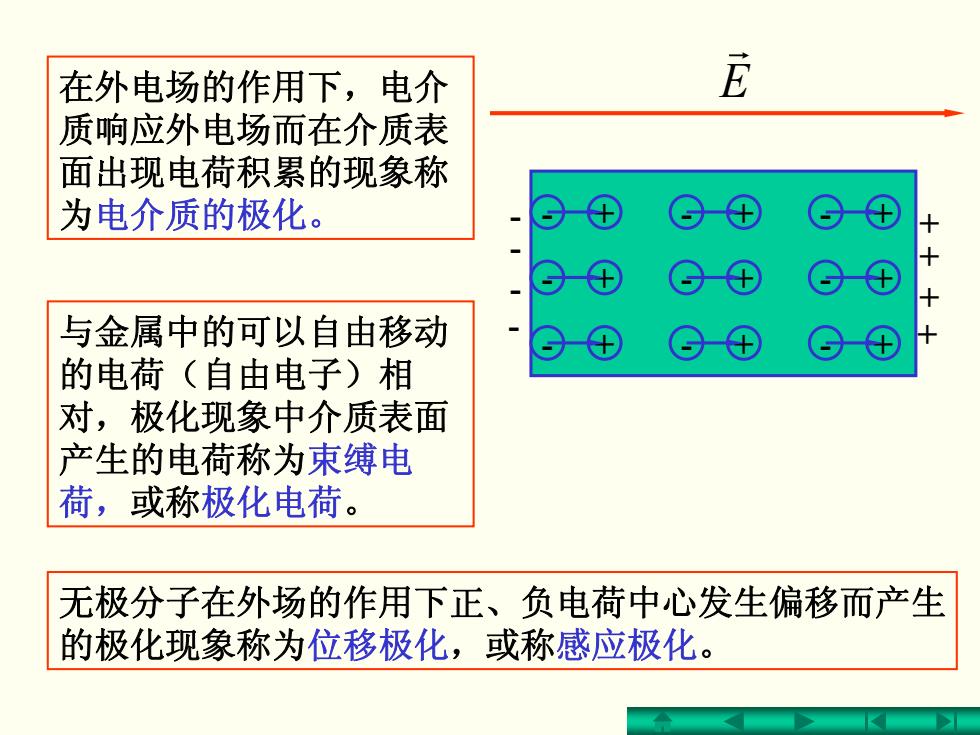
在外电场的作用下,电介 它 质响应外电场而在介质表 面出现电荷积累的现象称 为电介质的极化。 ©④ 与金属中的可以自由移动 的电荷(自由电子)相 对,极化现象中介质表面 产生的电荷称为束缚电 荷,或称极化电荷。 无极分子在外场的作用下正、负电荷中心发生偏移而产生 的极化现象称为位移极化,或称感应极化
在外电场的作用下,电介 质响应外电场而在介质表 面出现电荷积累的现象称 为电介质的极化。 与金属中的可以自由移动 的电荷(自由电子)相 对,极化现象中介质表面 产生的电荷称为束缚电 荷,或称极化电荷 。 无极分子在外场的作用下正、负电荷中心发生偏移而产生 的极化现象称为位移极化,或称感应极化 。 - - - - + + + + E r - + - + - + - + - + - + - + - + - +
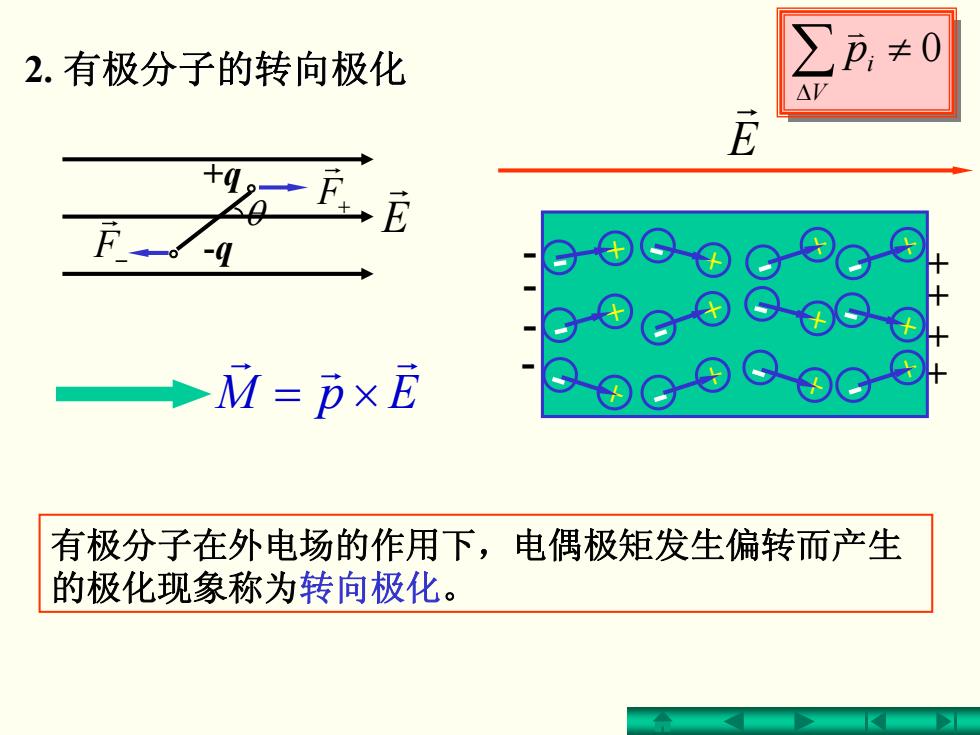
2.有极分子的转向极化 p,≠0 △V -0 →M=p×E 有极分子在外电场的作用下,电偶极矩发生偏转而产生 的极化现象称为转向极化
2. 有极分子的转向极化 有极分子的转向极化 有极分子在外电场的作用下,电偶极矩发生偏转而产生 的极化现象称为转向极化。 ∑ ≠ 0 ΔV i p v 。 。-q +q E r F+ r F − r θ EpM r r r ×= - - - - + + + + E r + - + - + - + - + - + - + - + - + - + - + - + -

三、电极化强度矢量 为了定量描述介质极化程 ∑, 度,引入电极化强度: p= △ (C.m-2) △V 介质内的总电场:E=E。+E 实验证明:对于各向同性的介质,当电场不太强时,介 质内任意点的电极化强度与该点的总电场强度成正比。 P=xeoE 一x。称为介质的电极化率 >当介质为各向同性的均匀介质 时,极化率为一纯(常)数
三、电极化强度矢量 三、电极化强度矢量 为了定量描述介质极化程 度,引入电极化强度: 度,引入电极化强度: V p P V i Δ = ∑Δ v v 介质内的总电场: 介质内的总电场: += EEE ′ v (C· m-2 ) v v 0 实验证明:对于各向同性的介质,当电场不太强时,介 质内任意点的电极化强度与该点的总电场强度成正比。 EPv v 0e = εχ —— χe 称为介质的电极化率 ¾当介质为各向同性的均匀介质 时,极化率为一纯(常)数
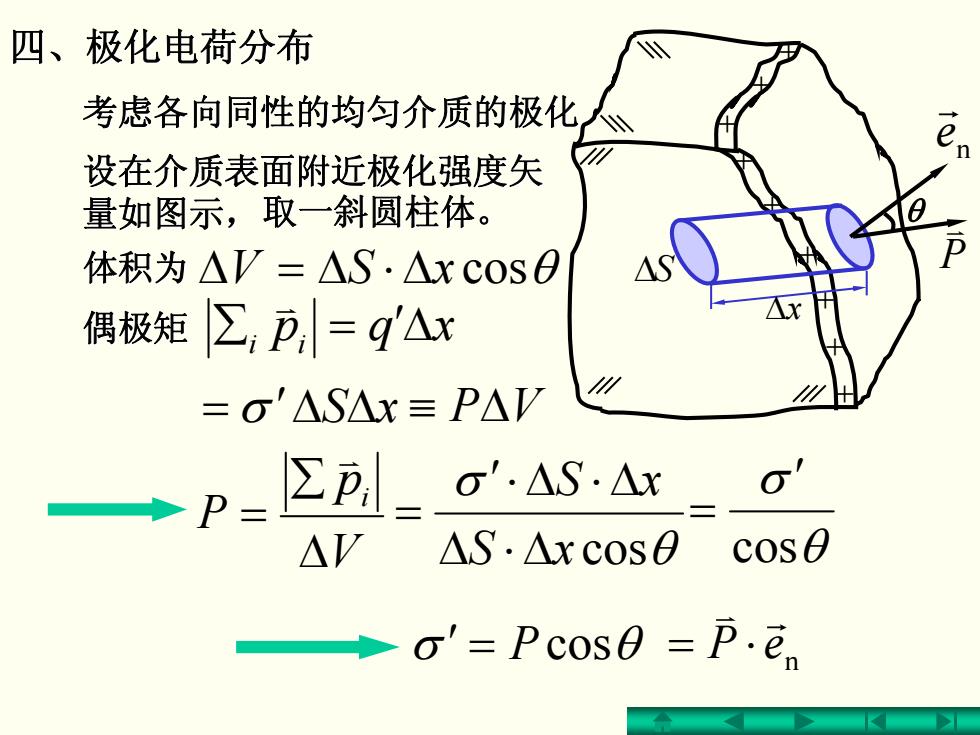
四、极化电荷分布 考虑各向同性的均匀介质的极化 设在介质表面附近极化强度矢 量如图示,取一斜圆柱体。 体积为△V=△S·△xCos0 偶极矩∑,p,=q△x =o'△S△x≡P△V —P=EEl_σ'ASAx O △V △S.△xcoS0cos0 'Pcose =p
四、极化电荷分布 四、极化电荷分布 考虑各向同性的均匀介质的极化 考虑各向同性的均匀介质的极化 Δ = Δ ⋅ΔxSV cosθ ii =∑ ′Δxqpv V p P i Δ ∑ = v σ′ = Pcosθ 体积为 n eP v r ⋅= 设在介质表面附近极化强度矢 设在介质表面附近极化强度矢 量如图示, = σ′Δ ΔxS θ σ xS cos xS Δ⋅Δ ′ ⋅Δ ⋅Δ = θ σ cos ′ = 偶极矩 取一斜圆柱体。 取一斜圆柱体。 ≡ ΔVP + + + + + + + + + Δx ΔS θ n e r P v