
第13章电介质 §13.1静电场中的电介质 §13.2介质中的高斯定理 §13.3介质边界两侧的静电场 §13.4静电场的能量
第 13 章 电介质 §13.2 介质中的高斯定理 介质中的高斯定理 §13.1 静电场中的电介质 静电场中的电介质 §13.4 静电场的能量 §13.3 介质边界两侧的静电场 介质边界两侧的静电场

§13.2介质中的高斯定理 一、介质中的静电场 有介质存在时,空间静电场的性质与自由电荷 (q)以及电介质的分布有关。 电介质的宏观电学性质可以由极化电荷() 代替。 空间总的静电场为: E=E。+E
+= EEE ′ r r r 0 §13.2 介质中的高斯定理 介质中的高斯定理 一、介质中的静电场 一、介质中的静电场 有介质存在时,空间静电场的性质与自由电荷 (q0)以及电介质的分布有关。 电介质的宏观电学性质可以由极化电荷(q') 代替。 空间总的静电场为:

*以平行板电容器为例讨论空间总的静电场* 平行板电容器 自由 电荷面密度为o 介质均匀极化,表面 出现束缚电荷士σ'。 O'=P 0 0 =Le8oE 内部的场由自由电荷 和束缚电荷共同产生 E=Ep+E
介质均匀极化,表面 出现束缚电荷± σ′。 内部的场由自由电荷 和束缚电荷共同产生 平行板电容器 自由 电荷面密度为 σ0 。 *以平行板电容器为例讨论空间总的静电场* σ 0 − σ 0 −σ′ σ′ χ e P r σ 0 − σ 0 −σ′ σ′ E0 r E' r = Pn σ ′ = χ ε 0e E += EEE ′ r r r 0
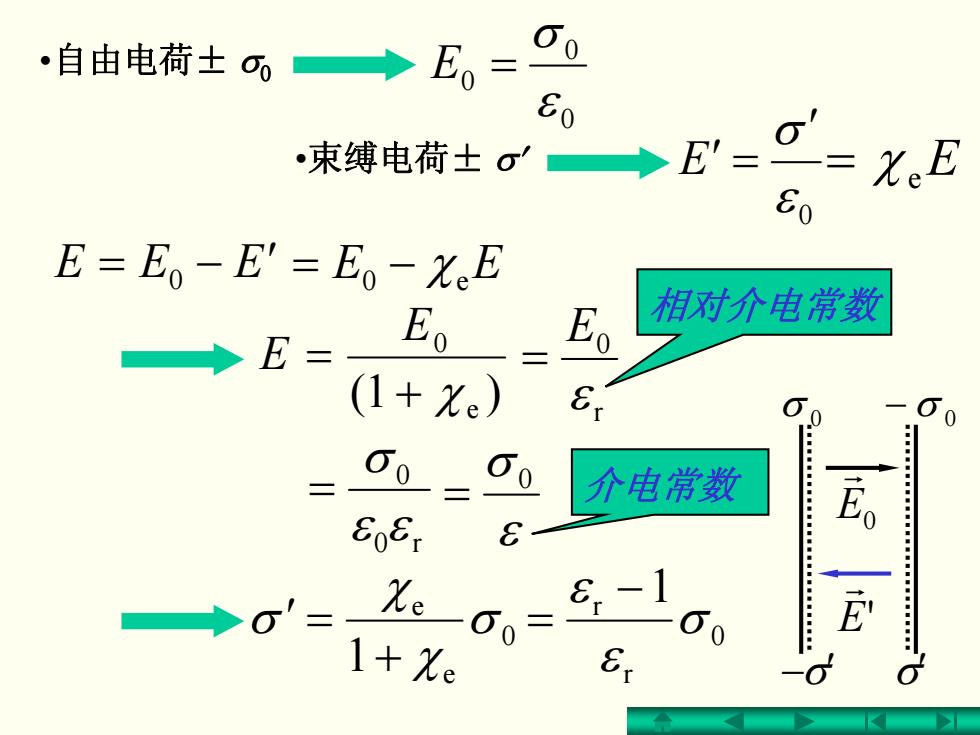
·自由电荷士σ o=o 80 束电荷士g→E'=g-XE 80 E=Eo-E'=Eo-xeE 相对介电常数 ◆E= Eo Eo (1+Xe) 介电常数 EoEr = 60 1+Xe
= − EEE ′ 0 )1( e 0 + χ = E E r0 0 εε σ = 0 0 0 ε σ E = 0 ε σ′ E′ = = − χe0 EE r 0 ε E = 相对介电常数 0 e e 1 σ χ χ σ + ′ = σ 0 − σ 0 −σ′ σ′ E0 r E' r •自由电荷± σ0 •束缚电荷± σ′ = χ eE 0 r r 1σ ε ε − = ε σ 0 = 介电常数

*充满介质时电容器的电容* •电容器无介质 时,自由电荷Qo →E0→AU→C,= △U0 •电容器充满介质 →△U= △U0 时,电场强度变小 E 9 △UU =6,C0 △U >介质中的场强E比真空中相应电荷分布的场强E,小, 而充满介质电容器的电容C比真空电容器的电容C,大。 —又称电容率
¾介质中的场强 E 比真空中相应电荷分布的场强 E0 小, 而充满介质电容器的电容 C 比真空电容器的电容 C0 大。 *充满介质时电容器的电容* •电容器无介质 时,自由电荷Q0 •电容器充满介质 时,电场强度变小 ——又称电容率。 ⇒ E0 ⇒ ΔU0 0 0 0 U Q C Δ = r 0 ε E E = r 0 ε U U Δ =Δ⇒ U Q C Δ = 0 0 0 r U Q Δ = ε C0r = ε 0 r C C ε =

二、介质中的高斯定理 真空中的高斯定理: 5E.d5=1Σq 介质中的高斯定理: dsga ∑g=-fp.ds
二、介质中的高斯定理 真空中的高斯定理: i S ∑=⋅ qSE ∫ 0 1 d ε v v 介质中的高斯定理: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∫ +=⋅ ∑∑ ' 1 d 0 S 内 S 内 S qqSE ε v v ∑ ∫ ⋅−= S S SPq r r d ' 内

fa-Σg5 人.GE+P)d5=∑9 u5-{2q- S内 S内 ∑9=人p.d5 S
∫ ∫ ⋅−∑=⋅ S S SPqSEv v v v d 11 d 0 0 εε ( ) qSPE S ∑=⋅+ ∫ v v v ε 0 d ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∫ +=⋅ ∑∑ ' 1 d 0 S内 S内 S qqSE ε v v ∑ ∫ ⋅−= S S SPq r r d ' 内

5529-nus f(oE+P)d5=∑q 定义电位移矢量: D=8oE+P D.d5-xg 一介质中的高斯定理
定义电位移矢量: 定义电位移矢量: PEDv v v ε 0 += ——介质中的高斯定理 介质中的高斯定理 qSDS ∑=⋅ ∫ v v d ∫ ∫ ⋅−∑=⋅ S S SPqSEv v v v d 11 d 0 0 εε ( ) qSPE S ∑=⋅+ ∫ v v v ε 0 d

讨论: Dds=Eq (1)介质中的高斯定理表明:电位移矢量 对任意封闭曲面的通量与该封闭曲面内的自 由电荷有关。 (2)电位移矢量是描述介质中电场性质 的辅助量,没有具体的物理意义。电场强 度是描述电场的基本物理量
qSDS ∑=⋅ ∫ v v d (1)介质中的高斯定理表明:电位移矢量 对任意封闭曲面的通量与该封闭曲面内的自 由电荷有关。 讨论: (2)电位移矢量是描述介质中电场性质 的辅助量,没有具体的物理意义。电场强 度是描述电场的基本物理量

(3)介质中的高斯定理包含了真空中的高斯定理。 p=0 ◆D=8E+p=8E foEd5=fD.d5=Eq → -439
(3)介质中的高斯定理包含了真空中的高斯定理。 P = 0 v Q PED v v v ε 0 += qSDS ∑=⋅ ∫ v v d qSES ∑=⋅ ∫ 0 1 d ε v v =⋅ ∫S SEv v d 0 ε E v 0 = ε