
第23章固体量子理论基础 §23.0引言 §23.1晶体 §23.2能带 §23.3导体绝缘体半导体
第 23 章 固体量子理论基础 §23.3 导体 绝缘体 半导体 §23.2 能带 §23.0 引言 §23.1 晶体
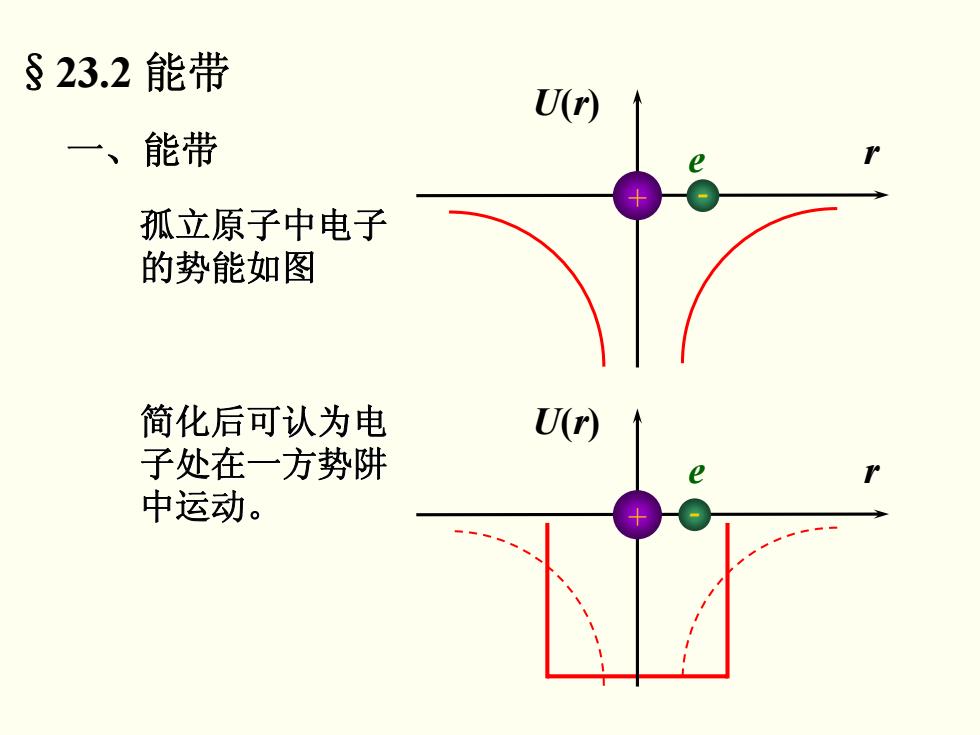
§23.2能带 U(r) 一、能带 孤立原子中电子 的势能如图 简化后可认为电 U(r) 子处在一方势阱 中运动
§23.2 能带 孤立原子中电子 孤立原子中电子 的势能如图 简化后可认为电 简化后可认为电 子处在一方势阱 子处在一方势阱 中运动。 U(r) + - e r U(r) + - e r 一、能带
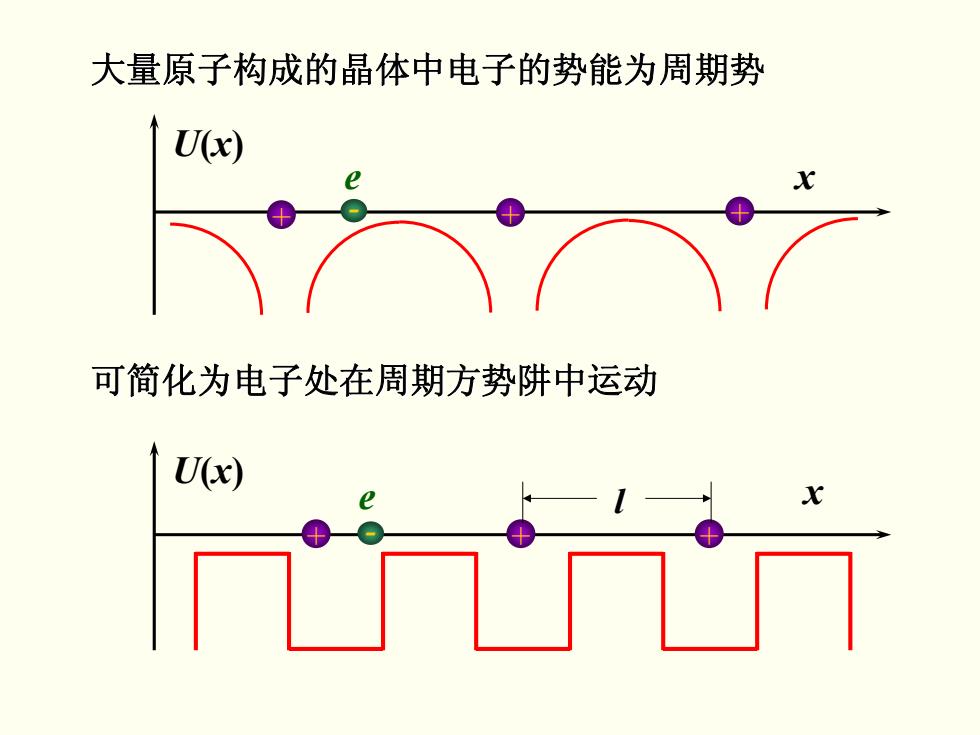
大量原子构成的晶体中电子的势能为周期势 U(x) 可简化为电子处在周期方势阱中运动 U(x)
大量原子构成的晶体中电子的势能为周期势 大量原子构成的晶体中电子的势能为周期势 可简化为电子处在周期方势阱中运动 可简化为电子处在周期方势阱中运动 U(x ) - e + x + + U(x ) x - e + + + l

电子处在单一方势阱中运动,能级是分立的 U(x) 电子处在周期性方势阱中运动,每一能级变 为一能带 U(x)
电子处在单一方势阱中运动,能级是分立的 电子处在单一方势阱中运动,能级是分立的 电子处在周期性方势阱中运动,每一能级变 电子处在周期性方势阱中运动,每一能级变 为一能带 U(x ) U(x )

例如:单个金属原子能级是分立的,有1s、2s、2p、 3s、3p、3d能级等等。 当金属原子相互靠近构成晶体时,每个能级变为能 带,分别为1s、2s、2p、3s、3p、3d能带等等
例如:单个金属原子能级是分立的,有 例如:单个金属原子能级是分立的,有1s 、2s 、2p 、 3s 、3p 、3d 能级等等。 当金属原子相互靠近构成晶体时,每个能级变为能 当金属原子相互靠近构成晶体时,每个能级变为能 带,分别为1s 、2s 、2p 、3s 、3p 、3d 能带等等。 + + + + + + + + + + + + e e e e e e e e e e e e

下面以例说明能带的成因 二、布洛赫(F.Bloch)定理 周期势场中运动的电子,周期性势能函数应满足周 期性条件 U(x)=U(x+n1) l为晶格常数(相邻格点的间距),为任意整数。 电子满足定态薛定谔方程为 2d2 2m dx2 +U(x)](x)=E(x) 布洛赫证明,定态波函数一定具有下列特征:
下面以例说明能带的成因 下面以例说明能带的成因 二、布洛赫 (F. Bloch) 定理 周期势场中运动的电子,周期性势能函数应满足周 周期势场中运动的电子, 期性条件 l 为晶格常数 (相邻格点的间距 ) , n 为任意整数。 U( x ) = U( x + n l ) 电子满足定态薛定谔方程为 电子满足定态薛定谔方程为 布洛赫证明,定态波函数一定具有下列特征: 布洛赫证明,定态波函数一定具有下列特征: )()()]( d d 2 [ 2 22 xExxU xm +− = ΦΦ h

D(x)=eiku(x) u(x+nl)=u(x) 布洛赫定理:在周期场中运动的电子波函数为 自由电子波函数Φ(x)与具有晶体结构周期的函 数山(x)的乘积,具有这种形式的波函数称为布 洛赫波函数或称为布洛赫波
布洛赫定理:在周期场中运动的电子波函数为 自由电子波函数 Φ (x ) 与具有晶体结构周期的函 数 u (x) 的乘积,具有这种形式的波函数称为布 洛赫波函数或称为布洛赫波 。 )(e)( i xux kx Φ = + = xunlxu )()(

三、克龙尼克一潘尼模型(Kronig-Penney Model) 考虑一粒子处在一维周期性方势阱中的运动 几几几「 在0<x<1区域势函数为1=b,+b2 0(0<x<b) U(x)= y。(b≤x≤)
三、克龙尼克—潘尼模型 (Kronig-Penney Model) 考虑一粒子处在一维周期性方势阱中的运动 在 0 < x < l 区域势函数为 = + bbl 21 ⎩⎨⎧ ≤≤ << = )( )0( 0 )( 10 1lxbV bx xU x O l b1 b2

在势阱内 dri +h=0 d2Φ 2mE 方2 D(x)=Aeikix+Be-ikix 在势垒内 2m-0 5 2m(E-Vo) 2 D2(x)=Ceikax+De-ik:x
2 2 1 2 h mE k = 在势阱内 在势垒内 0 d d 2 2 1 2 Φ =+ Φ k x xk xk BAx 1 1 i i 1 ee)( − Φ += 0 d d 2 2 2 2 Φ =+ Φ k x 2 2 0 2 )(2 h VEm k − = xk xk DCx 2 2 i i 2 ee)( − Φ +=

由布洛赫定理 中(x)=e4(x) D(x)=eu(x) 且有 4(0)=h2(0), du dx x=0 dx x=/ 再结合波函数的标准条件(单值、有限、连续)可得 coscos +好 sink b sink,b,coskl 2k k 由于-1<cos kl<1,对等式左侧的k、k(或E)附 加了限制:
再结合波函数的标准条件(单值、有限、连续)可得 由布洛赫定理 )(e)( 1 i 1 xux kx Φ = 且有 由于 -1<cos kl <1 ,对等式左侧的 k 1 、 k2 ( 或E) 附 加了限制: )(e)( 2 i 2 xux kx Φ = x lx x u x u uu = = = = d d d d ),0()0( 2 0 1 1 2 klbkbk kk kk bkbk sinsin cos 2 coscos 2211 21 2 2 2 1 2211 = + −