
第4章·动量和角动量
第 4 章 动量和角动量

第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量

§4.1动量定理 动量守恒定律 一、动量与冲量 动量: p=mv 单位:kg'm's-1 牛顿第二定律: F d(mv) 0)=m ma dt t 冲量:作用力与作用时间的乘积。 恒力的冲量:了=F.(t2-t) 单位:Ns 变力的冲量: 7=()-d >冲量是反映力对时间的累积效应的物理量
一、动量与冲量 vmp r r = 单位:kg·m·s-1 ¾ 冲量是反映力对时间的累积效应的物理量。 冲量:作用力与作用时间的乘积。 恒力的冲量: )( 12 −⋅= ttFI r r 变力的冲量: ∫ ⋅= 21 d)( tt ttFIr r 单位:N·s 牛顿第二定律: am t v mF t vm F t m r r r r r ⎯= ⎯ → ==⎯ = d d d )(d 0 dd 动量: §4.1 动量定理 动量守恒定律

二、质点动量定理 由牛顿运动定律: F= d(mv) dp di dt 动量定理的微分式: dp=F.dt 如果力的作用时间从t,→t,质点动量从p0→p 则: i='F.dt=p-p。=m-m, 质点动量定理:质点在运动过程中,所受合外力的冲 量等于质点动量的增量
二、质点动量定理 由牛顿运动定律: t p t vm F d d d )(d r r r == ⋅= dd tFp r r 如果力的作用时间从 ,质点动量从 则: → tt0 pp v v 0 → 0 0 0 d vmvmpptFI t t r r r r r r −=−=⋅= ∫ 质点动量定理:质点在运动过程中,所受合外力的冲 量等于质点动量的增量。 动量定理的微分式:

说明≤ i=F.dt=p-p。=mv-mg (①)反映了力在时间上的累积作用对质点产生的效果。 (2)动量定理中的动量和冲量都是矢量,符合矢量叠加 原理。或以分量形式进行计算。 1.=∫F.d/=mv.-mvo I,=F,dt=m,-mv,o I.=[,F.dt=mv:-mv.o
(2) 动量定理中的动量和冲量都是矢量,符合矢量叠加 原理。或以分量形式进行计算。 ∫ ∫ ∫ −== −== −== t t z z zz t t y y yy xx t t x x mvmvtFI mvmvtFI mvmvtFI 0 0 0 0 0 0 d d d (1) 反映了力在时间上的累积作用对质点产生的效果。 说明 0 0 0 d vmvmpptFI t t r r r r r r −=−=⋅= ∫
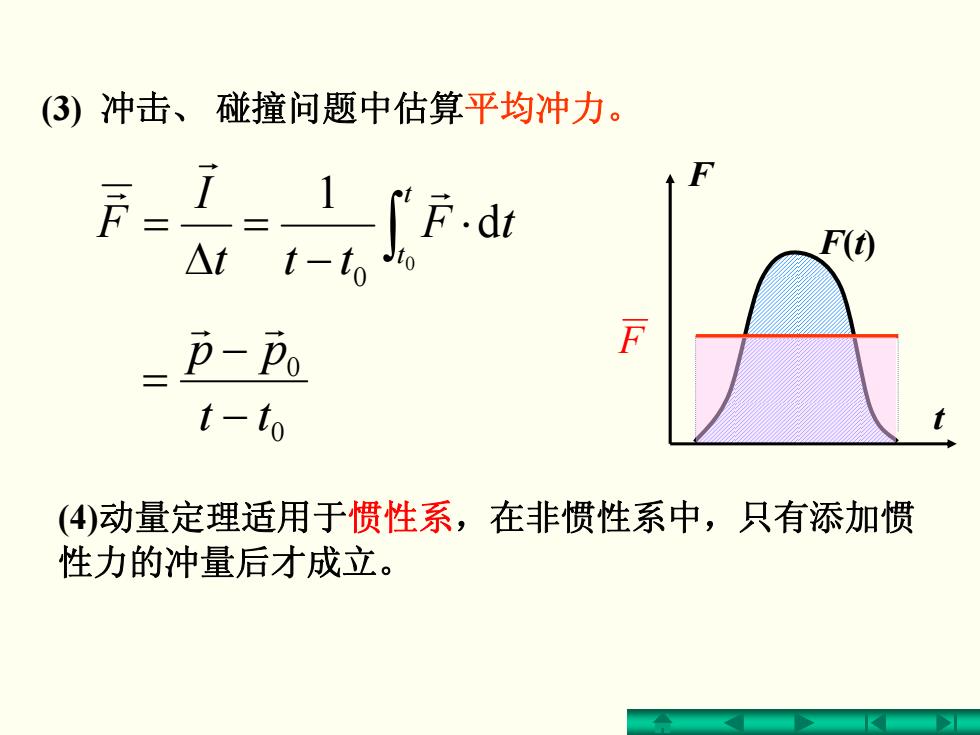
(3)冲击、碰撞问题中估算平均冲力。 F(t) =p-p6 t-to (4)动量定理适用于惯性系,在非惯性系中,只有添加惯 性力的冲量后才成立
(3) 冲击、 碰撞问题中估算平均冲力。 ∫ ⋅ − = Δ = tt tF tttI F 0 d 1 0 r r r (4)动量定理适用于惯性系,在非惯性系中,只有添加惯 性力的冲量后才成立。 F(t) F t F 0 0 t t p p − − = r r

[例4-1]=10kg木箱,在水平拉力作用下由静止开始运 动,拉力随时间变化如图。已知木箱与地面摩擦系数为4 =0.2,求: (1)仁4秒时刻木箱速度; (2)仁7秒时刻木箱速度; (3)仁6秒时刻木箱速度。 解:(①)根据动量定理: FN F'dt=mv,-mvo 30 →(F-umg)△t=mv4 0 4 7 t/s -5ga-(20-02×10x4=0ms)
解: 04 4 0 ′d −= mvmvtF ∫ 4 −⇒ μ )( Δ = mvtmgF tg m F v4 μ )( Δ−= (1) 根据动量定理: 30 0 47 t/s F/N [例4-1] m=10 kg木箱,在水平拉力作用下由静止开始运 动,拉力随时间变化如图。已知木箱与地面摩擦系数为μ =0.2,求: (1) t=4 秒时刻木箱速度; (2) t=7 秒时刻木箱速度; (3) t=6 秒时刻木箱速度。 m F r )m/s(44)102.0 1030 ( =××−=

(2) F'dt=mv,-mva (F=F-umg) F=70-10t (4≤t≤7) my =[(70-10t-jmg)dt+mva ,=(5-t)dt+4=2.5(m/s) EN 30 v6=(5-t)dt+4=4(m/s) 47t/s
d )2( 47 7 4 ′ −= mvmvtF ∫ = − ≤ ttF ≤ )74( 1070 4 7 4 mv7 d)1070( +−−= mvtmgt ∫ μ )m/s(5.24d)5( 7 4 7 =+−= ∫ ttv )m/s( 44d)5( 6 4 6 =+−= ∫ ttv 30 0 47 t/s F/N ( ′ = − μmgFF )

[例4-2】质量为的行李,垂直地轻放在传送带上,传送 带的速率为v,它与行李间的摩擦系数为业,试计算:(1) 行李将在传送带上滑动多长时间?(2)行李在这段时间内运 动多远?(③)有多少能量被摩擦所耗费? 解:(1)以地面为参照系 Ft=umgt mv-0 →t=v/g 2)由质点动能定理 A=Fx=mgx=5mv2-0→x= 2 2ug (或:x= -ai 2=
[例4-2] 质量为m的行李,垂直地轻放在传送带上,传送 带的速率为v,它与行李间的摩擦系数为μ, 试计算:(1) 行李将在传送带上滑动多长时间? (2) 行李在这段时间内运 动多远? (3) 有多少能量被摩擦所耗费? f = μ = mvmgttF − 0 (1) 以地面为参照系 (2) 由质点动能定理 0 2 1 2 f μ mvmgxxFA −=== 解: (或: == L ) 2 21 atx m O x v =⇒ μgvt g v x 2μ 2 =⇒
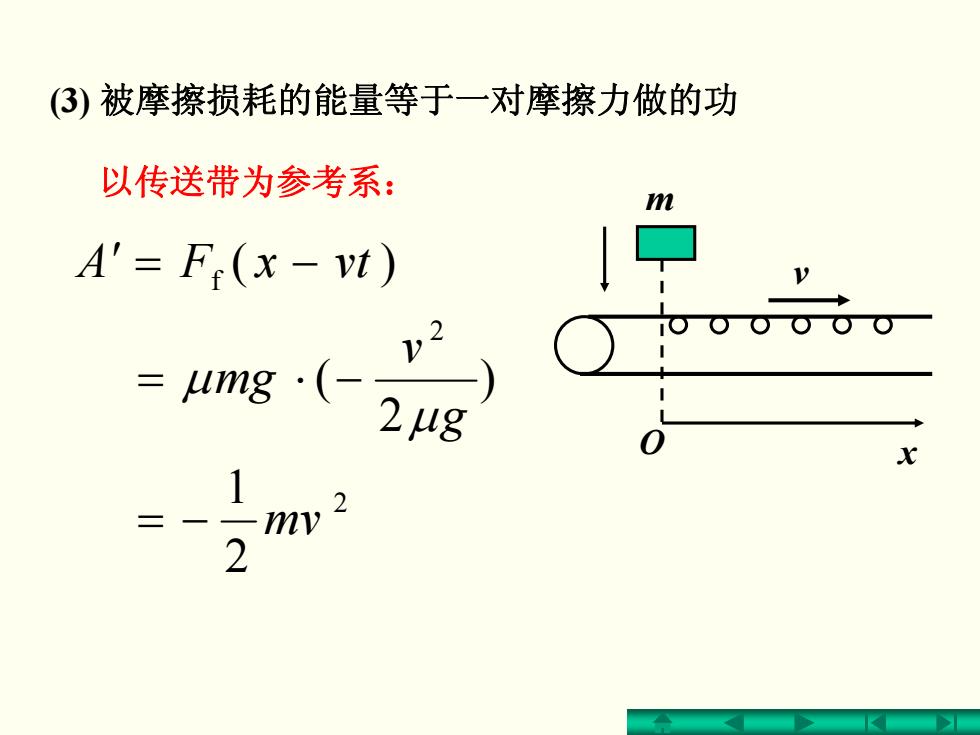
(3)被摩擦损耗的能量等于一对摩擦力做的功 以传送带为参考系: A'=F(x-vt) =μmg·(-24g my 2
m O x v (3) 被摩擦损耗的能量等于一对摩擦力做的功 )(f ′ = − vtxFA 以传送带为参考系: 2 2 2 1 ) 2 ( mv g v mg −= −⋅= μ μ