
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振

§6.5垂直简谐振动的合成 一、同频率垂直简谐振动的合成 x=A cos(@t+) y=4 cos(@i+p2) 0 X cos@tcosp-sinotsinp A y cos@tcoso2-sin@tsin A 2xy A A4 cos(o2-0)=sin(2-)
cos( ) = 2 ω +ϕ 2 tAy 2 2 2 t tsinsincoscos ϕωϕω Ay = − )cos( = 1 ω +ϕ1 tAx 1 1 1 t tsinsincoscos ϕωϕω Ax = − )(sin)cos( 2 12 2 12 21 2 2 2 2 1 2 −+ −=− ϕϕϕϕ AAxy Ay Ax 一、同频率垂直简谐振动的合成 §6.5 垂直简谐振动的合成 y o x

>结论:两相互垂直同频率简谐振动的合成其振动轨 迹一般情况下为一椭圆(又称“椭圆振动”)。 椭圆轨迹的形状取决于振幅和相位差。 讨论: (I)p2-0=0(或2k元) x2 + 2y=0 A =0 y=A 斜率: A A
¾结论:两相互垂直同频率简谐振动的合成其振动轨 迹一般情况下为一椭圆(又称“椭圆振动”)。 椭圆轨迹的形状取决于振幅和相位差。 讨论: 0 2 21 2 2 2 2 1 2 =−+ AA xy A y A x 0 2 21 = ⎟⎟⎠⎞ ⎜⎜⎝⎛ − Ay Ax (1) y x o 0 1 2 1 2 = > A A x A A y 斜率: 2(0 π ) 12 ϕ ϕ =− 或 k
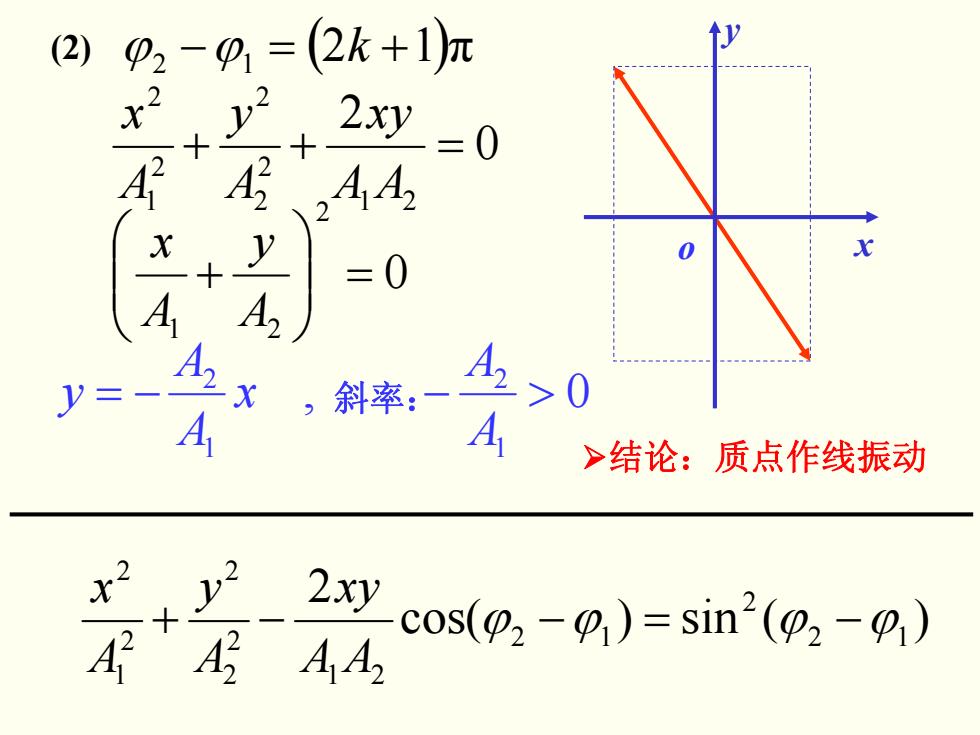
(2) p2-0,=(2k+1)元 1 A 2xy=0 A4 =0 y= ,斜率: A270 A A >结论:质点作线振动 x2 AA AA 2yc0s(m,-0,)=sin2(0,-0)
)(sin)cos( 2 12 2 12 21 2 2 2 2 1 2 −+ −=− ϕϕϕϕ AAxy A y A x ϕ − ϕ12 = ( k +12 ) π 0 2 21 2 2 2 2 1 2 =++ AA xy A y A x 0 2 21 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + A y A x ¾结论:质点作线振动 (2) x y o , 0 1 2 1 2 −= >− A A x A A y 斜率:

a-物-引或+ =1 A >结论:质点振动轨迹为正椭圆 (若y超前x,顺时针,称为右旋; 若x超前y,逆时针,称为左旋。) x2y2 2ycos(0,-9,)=sin2(p,-9,) AA
1 2 2 2 2 1 2 =+ A y A x ¾结论:质点振动轨迹为正椭圆 (若 y 超前x,顺时针,称为右旋; 若 x 超前y,逆时针,称为左旋。) (3)当: )(sin)cos( 2 12 2 12 21 2 2 2 2 1 2 −+ −=− ϕϕϕϕ AAxy Ay Ax y o x ( ) ⎥⎦⎤ ⎢⎣⎡ =− + 2π 12 2π 12 ϕϕ 或 k

两垂直简谐振动在不同相位差时的合成 3π p2-01=0 元 4 5π 3π 7π 2π 9π 2 4 2A2 2A→
9 两垂直简谐振动在不同相位差时的合成 ϕ −ϕ12 = 0 4 π 2 π 4 3π π 2A2 2 A1 4 5π 2 3π 4 7π 2π 4 9π
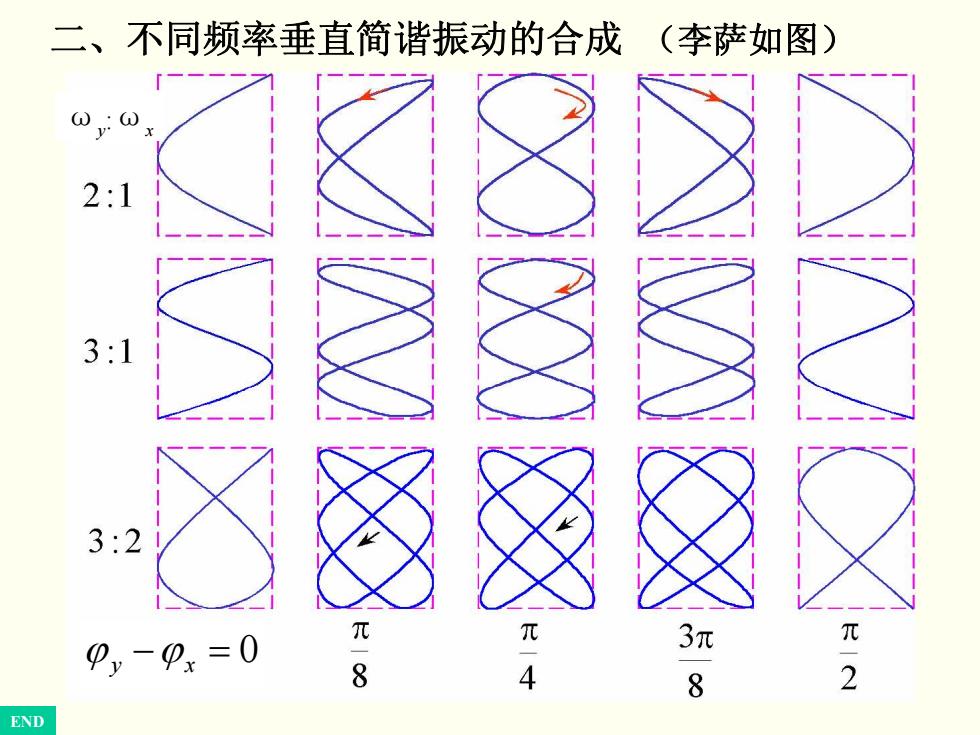
二、不同频率垂直简谐振动的合成(李萨如图) wy0 2:1 31 :2 y-x=0 3元 8 8 2 END
END 二、不同频率垂直简谐振动的合成 (李萨如图) ω y:ωx − = 0 ϕ ϕ xy