
第7章狭义相对论基础 §7.1经典力学的困难 §7.2狭义相对论的基本假设 §7.3洛伦兹变换 §7.4狭义相对论的时空观 §7.5相对论力学 §7.6狭义相对论的进一步讨论
第 7 章 狭义相对论基础 §7.1 经典力学的困难 经典力学的困难 §7.2 狭义相对论的基本假设 §7.5 相对论力学 §7.4 狭义相对论的时空观 狭义相对论的时空观 §7.3 洛伦兹变换 §7.6 狭义相对论的进一步讨论
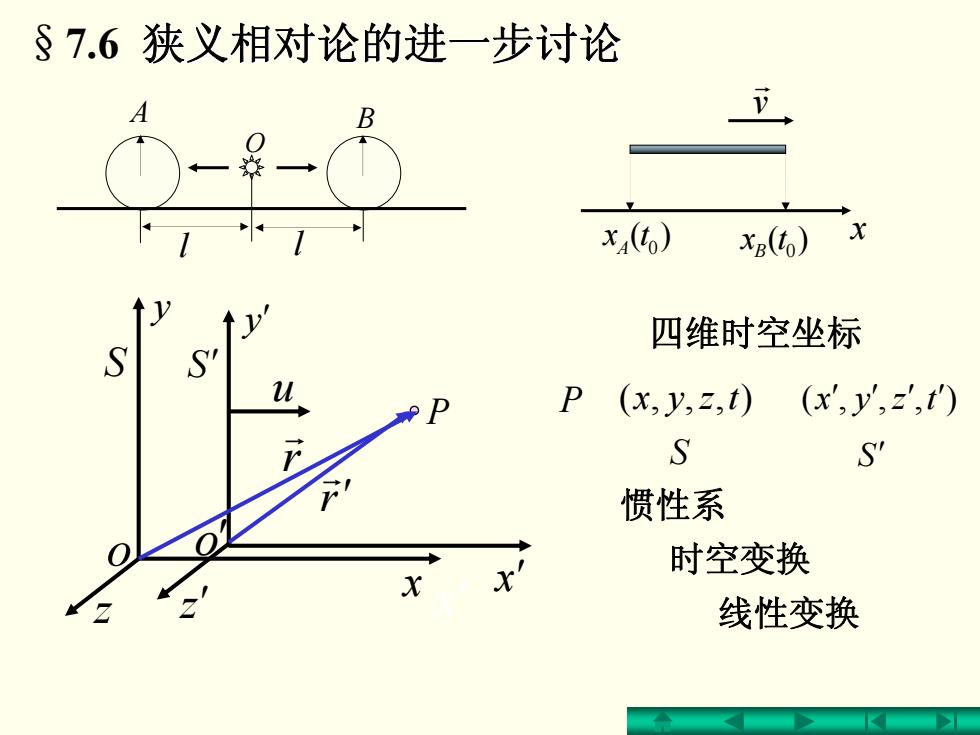
§7.6狭义相对论的进一步讨论 x4() x() 四维时空坐标 P (x,y,z,t) (x',y',z',t) S S 惯性系 时空变换 线性变换
P r r o ′ S′ u x ′ x o S y r ′ r y ′ z z ′ x ′ v r )( 0txA )( 0txB x O A B l l P (x, y,z,t) (x′, y′,z′,t′) S S′ 惯性系 时空变换 四维时空坐标 线性变换 §7.6 狭义相对论的进一步讨论
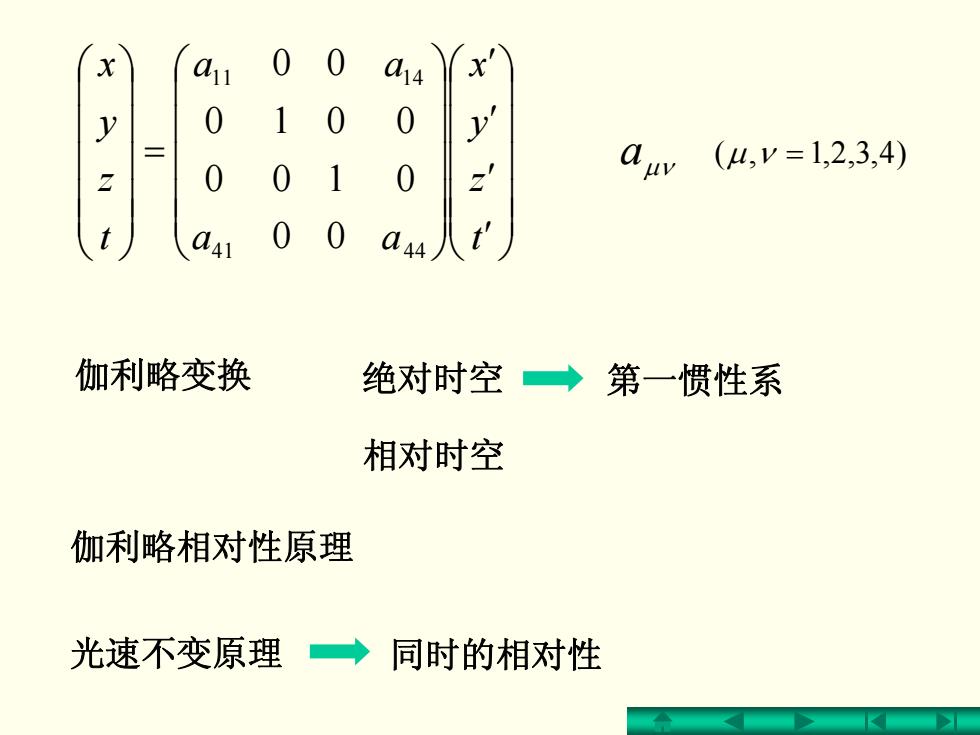
a14 y (4,V=1,2,3,4) 伽利略变换 绝对时空→第一惯性系 相对时空 伽利略相对性原理 光速不变原理◆ 同时的相对性
⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ ′′′′ ⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ =⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ tzyx a a a a tzyx 41 44 11 14 00 0100 0010 00 aμν μ ν = )4,3,2,1,( 伽利略变换 绝对时空 相对时空 伽利略相对性原理 第一惯性系 光速不变原理 同时的相对性

两个事件P、P2 在S系中的时空坐标分别为(x1,y1,21,41)和(x2,y2,22,2) 在S系中的时空坐标分别为(x,,,)和(x2,y2,2,2) 事件P、P之间的间隔 (4S)2=(x)2+(y)2+(正)2+(ic)2 由洛伦兹变换 →(AS)2=(△S")2 在坐标变换下,间隔保持不变,它是洛伦兹变换的不变量 类比:三维欧氏空间中两点的距离是坐标变换的不变量 构建四维时空坐标 x1=x,X2=y,x3=2,x4=1Ct
事件 之间的 、PP 21 间隔 在坐标变换下,间隔保持不变,它是洛伦兹变换的不变量 在S系中的时空坐标分别为 tzyx 1111 ),,,( 和 ),,,( 2222 tzyx 在 系中的时空坐标分别为 tzyx 1111 ),,,( 和 两个事件P1、P2 ′ ′ ′ ′ ),,,( 2222′ ′ ′ tzyx ′ S′ ( )2 2 2 2 2 +++= ΔΔΔΔΔ tczyxS )i()()()( 由洛伦兹变换 2 2 Δ=Δ SS ′)()( 类比:三维欧氏空间中两点的距离是坐标变换的不变量 构建四维时空坐标 i,,, ctxzxyxxx = = = 4321 =
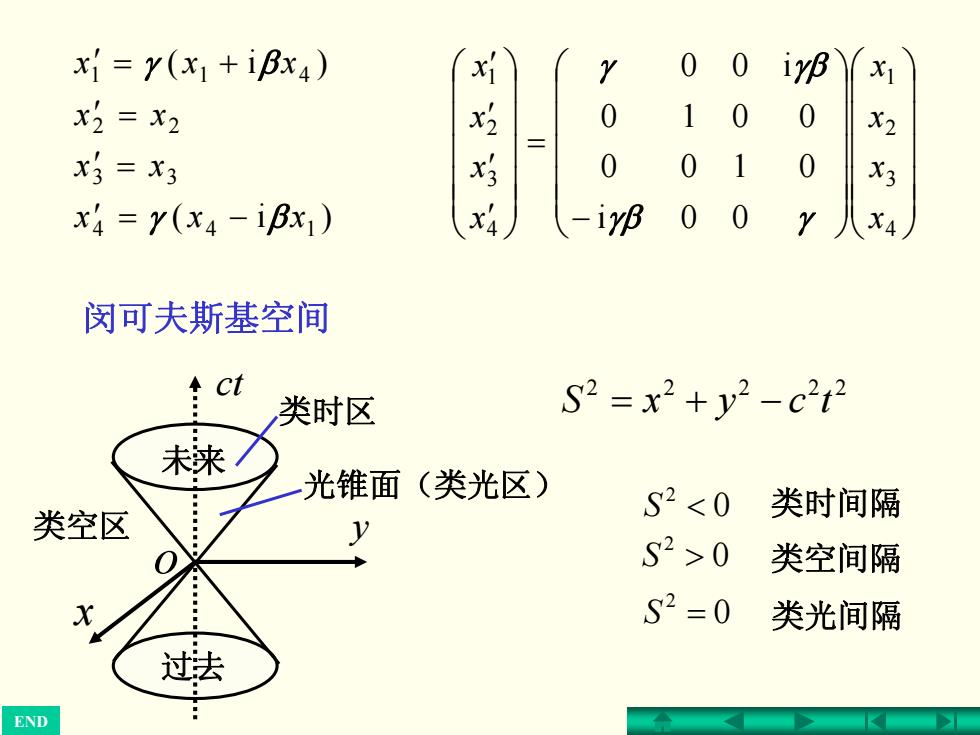
x=r(x1+iBx4) Y 0 0 irB x2=X2 0 1 0 0 x3=X3 0 0 X3 x4=y(x4-iBx) -iy30 X4 闵可夫斯基空间 类时区 S2=x2+y2-c212 未来 光锥面(类光区) 类空区 S20 类空间隔 S2=0 类光间隔 过去
)i( )i( 4 14 33 22 1 41 xxx xx xx xxx βγ γ β ′ −= ′ = ′ = ′ = + ⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ − =⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ ′′′′ 4321 4321 00i 0100 0010 i00 xxxx xxxx γβ γ γ γβ 闵可夫斯基空间 x o y ct 未来 过去 类空区 类时区 光锥面(类光区) 22222 −+= tcyxS 0 2 S 0 2 S = 类时间隔 类空间隔 类光间隔 END