
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振

§6.2简谐振动运动学 一、周期频率和角频率 周期T:完成一次全振动所经历的时间。 频率v:单位时间内完成全振动的次数。V=1/T Acos[o(t+T)+]=Acos(@t+p) 2元 0T=2元, =2元V T 角频率(或称圆频率) 2元 = m T= 2元1 k
一、周期 频率和角频率 周期 T:完成一次全振动所经历的时间。 频率 ν :单位时间内完成全振动的次数。 ν =1/ T ω :角频率 (或称圆频率) m k ω = k m T 2 π 21 π === ων ω + + ϕ = ωtATtA + ϕ)cos(])(cos[ ω ω 2 π ν 2 π = 2 π , == T T §6.2 简谐振动运动学

T、y或o分别称为谐振子的固有周期、固有频率 和固有角频率 故:x=Ac0S(ot+p) 2元 -Acos() =Ac0s(2πt+0) 其中A即位移的最大值,称为振幅 T的单位:s(秒)、v的单位:Hz(赫兹) o的单位:rad/s(弧度每秒)
T、 ν 或ω分别称为谐振子的固有周期、固有频率 和固有角频率 故: = ωtAx +ϕ)cos( 其中A即位移的最大值,称为振幅 T 的单位: s (秒) 、ν 的单位: Hz (赫兹) ω 的单位: rad/s(弧度每秒) ) 2π = cos( t +ϕ T A = 2cos( πνtA +ϕ)

二、相位 (1)(ot+p)是t时刻的相位 (2)p是t=0时刻的相位一 初相位 由仁0;=x0,=y得 2 A= 2 Vo tan⑩=- WXo
二、相位 (1) (ω t +ϕ )是 t 时刻的相位 (2) ϕ 是t =0时刻的相位 ——初相位 由t=0;x=x0,v=v0 得 2 2 2 0 0 ω v xA += 0 0 tan x v ω ϕ −=
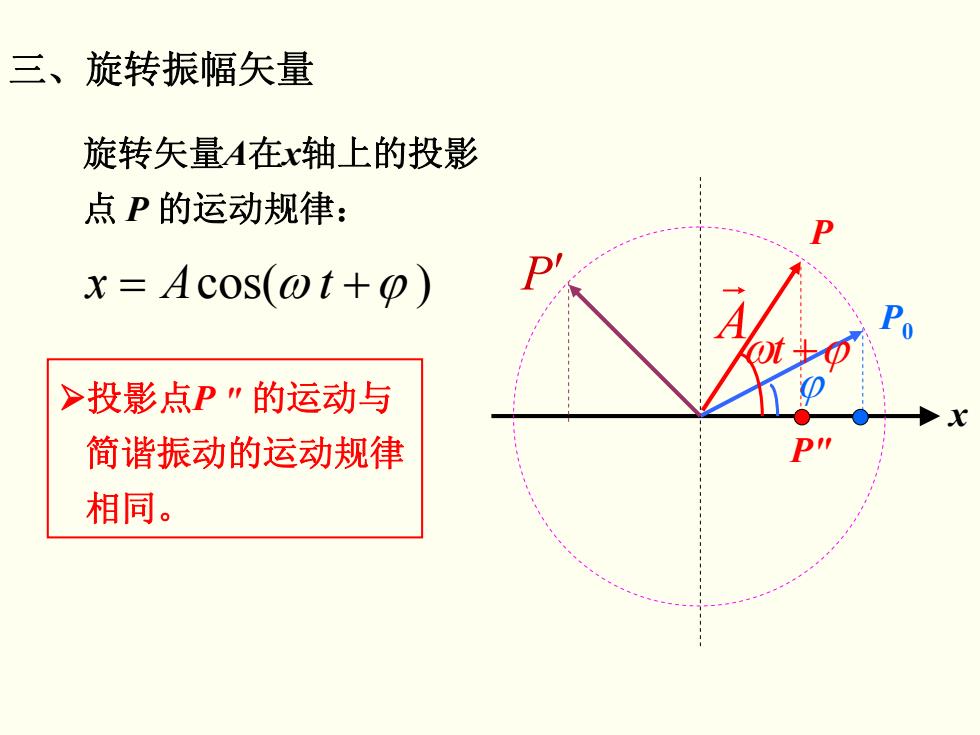
三、旋转振幅矢量 旋转矢量A在x轴上的投影 点P的运动规律: D x=Acos(ot+0) >投影点P"的运动与 简谐振动的运动规律 相同
三、旋转振幅矢量 旋转矢量A 在x轴上的投影 点 P 的运动规律: = ω tAx + ϕ )cos( ¾投影点P " 的运动与 简谐振动的运动规律 相同。 P0 P P ′ A r x ϕ ωt + ϕ P
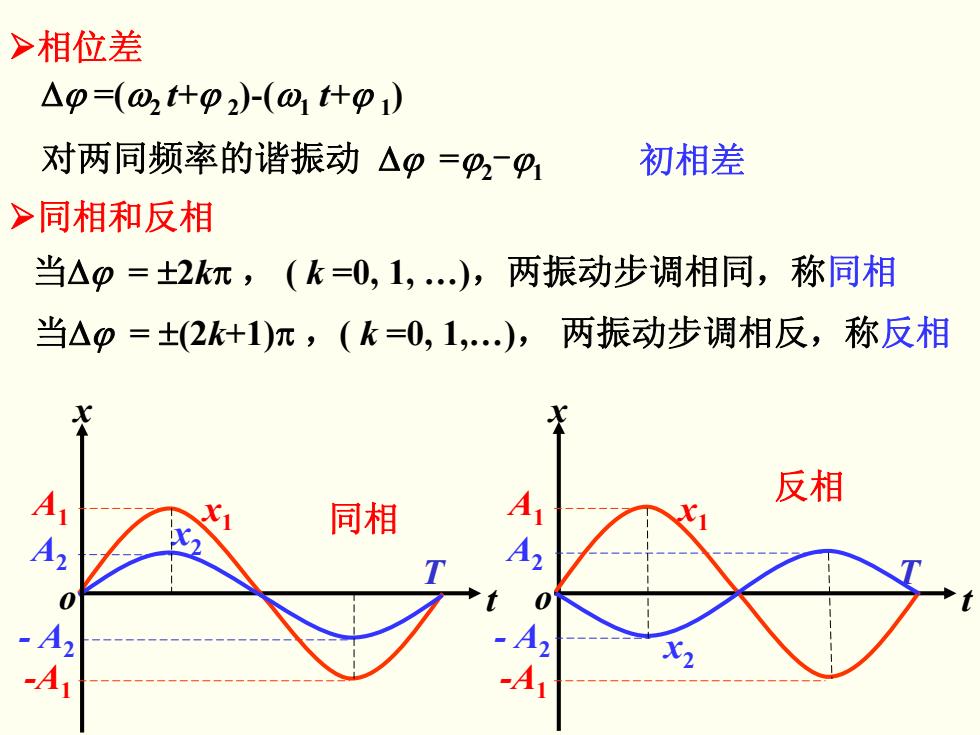
>相位差 △p=(02t什p2)-(01什p1) 对两同频率的谐振动△p=p291 初相差 >同相和反相 当△p=±2k红,(k=0,1,…),两振动步调相同,称同相 当△p=±(2k+1)元,(k=0,1,),两振动步调相反,称反相 反相 同相
Δϕ =(ω2 t+ϕ 2)-(ω1 t+ϕ 1) ¾相位差 对两同频率的谐振动 Δϕ =ϕ2-ϕ1 初相差 ¾同相和反相 当Δϕ = ±2kπ , ( k =0, 1, …),两振动步调相同,称同相 当Δϕ = ±(2k+1)π ,( k =0, 1,…), 两振动步调相反,称反相 o A1 -A1 A2 - A2 x1 x2 T 同相 t x x o A1 -A1 A2 - A2 x1 x2 T t 反相
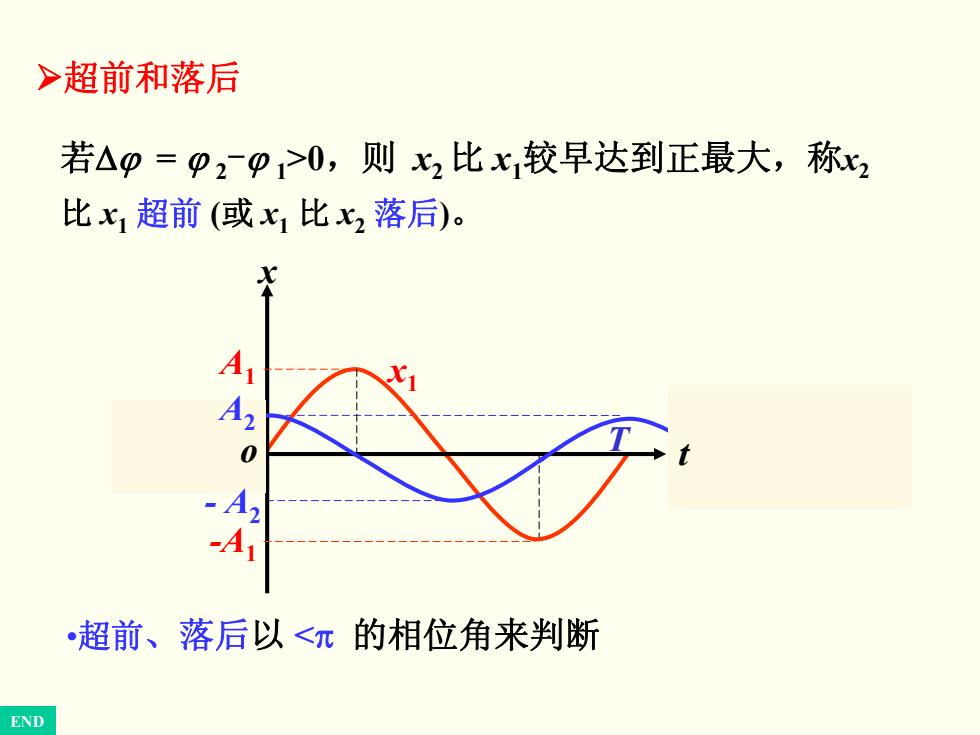
>超前和落后 若△p=p2p>0,则2比x较早达到正最大,称2 比七1超前(或x1比x2落后)。 日内味 •超前、落后以<π的相位角来判断 END
¾超前和落后 若Δϕ = ϕ 2-ϕ 1>0,则 x2 比 x1较早达到正最大,称x2 比 x1 超前 (或 x1 比 x2 落后)。 •超前、落后以 <π 的相位角来判断 A1 x1 T x o t A2 - A2 -A1 END