
第3章 机械能和功 §3.1功质点动能定理 §3.2保守力非保守力耗散力 §3.3质点在保守力场中的势能 §3.4质点系的势能 §3.5功能原理 能量守恒定律
第 3 章 机械能和功 §3.1 功 质点动能定理 §3.2 保守力 非保守力 耗散力 §3.3 质点在保守力场中的势能 §3.4 质点系的势能 §3.5 功能原理 能量守恒定律

§3.5功能原理能量守恒定律 一、质点系的动能定理 设第i个质点所受外力的功为A,。,内力的功为4,初 速度为V0,末速度为y;。 2 ∑A+∑4=∑2m-∑m呢 ∑A。=A,外力对质点系做的总功。 ∑A1=A,内力对质点系做的总功
一、质点系的动能定理 2 0 2 Ie 2 1 2 1 iii ii ii −=+= vmvmAAA 2 0 2 e I 2 1 2 1 ii i ii i i i i i =+ −∑∑∑∑ vmvmAA 设第 i 个质点所受外力的功为 ,内力的功为 , 初 速度为 , 末速度为 。 Aie AiI i0 v i v , AA ee i i = §3.5 功能原理 能量守恒定律 ∑ , AA II i ∑ i = 外力对质点系做的总功。 内力对质点系做的总功

∑=E, 质点系的末态总动能。 ∑)m呢=E0,厦点系的初态总动能。 A+A=E'k-Eko=AEk 质点系的动能定理:所有外力和内力对系统所作的 功之和等于系统总动能的增量
质点系的动能定理: 所有外力和内力对系统所作的 功之和等于系统总动能的增量。 + = − 0kkIe = ΔEEEAA k , 2 1 k 2 ii Evm i ∑ = , 2 1 0k 2 ii 0 Evm i ∑ = 质点系的末态总动能。 质点系的初态总动能
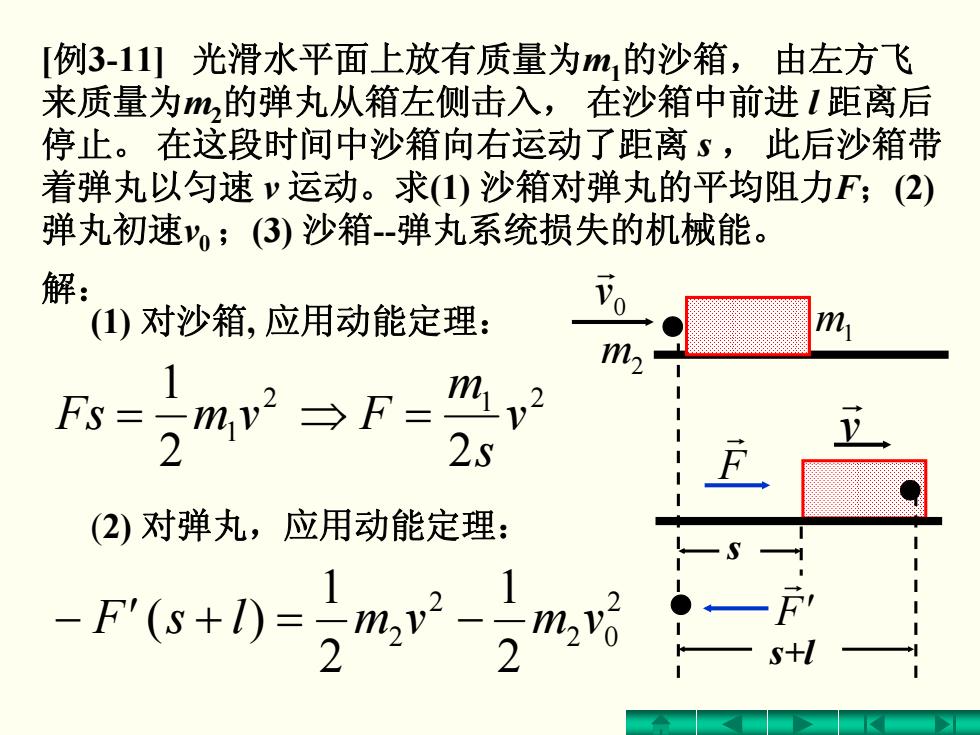
[例3-11]光滑水平面上放有质量为m,的沙箱,由左方飞 来质量为m,的弹丸从箱左侧击入,在沙箱中前进1距离后 停止。在这段时间中沙箱向右运动了距离s,此后沙箱带 着弹丸以匀速v运动。求(1)沙箱对弹丸的平均阻力F;(2) 弹丸初速;(3)沙箱-弹丸系统损失的机械能。 解 ()对沙箱,应用动能定理: m2 24 2s (2)对弹丸,应用动能定理: -6+小-2m2- 2 S+
[ 例3-11] 光滑水平面上放有质量为 m 1的沙箱, 由左方飞 来质量为 m 2的弹丸从箱左侧击入, 在沙箱中前进 l 距离后 停止。 在这段时间中沙箱向右运动了距离 s , 此后沙箱带 着弹丸以匀速 v 运动。求(1) 沙箱对弹丸的平均阻力 F;(2) 弹丸初速 v0 ;(3) 沙箱--弹丸系统损失的机械能。 (2) 对弹丸,应用动能定理: 2 1 2 1 = vmFs 2 02 2 2 2 1 2 1 − ′ )( −=+ vmvmlsF (1) 对沙箱, 应用动能定理: 解: m 1 m 2 • 0 v r v r s+l • F r ′ s • F r 1 2 2 v s m F =⇒

F'=F→V0=V m(s+ 2+1 (3)机械能变化: 2 m2 2 =Fs-F(s+1) -F=- %12 2s 一对非保守内力(耗散力)做 负功,使系统动能减少
(3) 机械能变化: 2 02 2 21 2 1 )( 21 −+=Δ vmvmmE 一对非保守内力(耗散力)做 负功,使系统动能减少。 m1 m2 • 0 v r v r s+l • F r ′ s • F r 1 )( 2 1 0 + + ′ =⇒= sm lsm vvFF = − + lsFFs )( 1 2 2 lv s m Fl −=−=

二、功能原理 保守内力的总功AC 内力的总功A 非保守内力的总功A A+AN+AC=Ek-Ek0=△Ek A=-(E。-E0)=-AE, A+A=(E+E,)-(Ew+E0) =E-E,=△E 质点系的功能原理:质点系在运动过程中,所有外 力的功和非保守内力的功的总和等于系统机械能的 增量
二、功能原理 保守内力的总功 ACI 非保守内力的总功 ANI 内力的总功 AI + NIe + CI = − 0kk = ΔEEEAAA k CI p0p p = − − )( = −ΔEEEA )()( + = + − +EEEEAA p0k0pkNIe = − 0 =ΔEEE 质点系的功能原理: 质点系在运动过程中,所有外 力的功和非保守内力的功的总和等于系统机械能的 增量

4+A=(Es+Ep)-(Eko+Epo) 说明 1.明确系统及初、末状态。 2.适用于惯性系。 3.若A=0,A=0 △E=0→Ek+E。=Eko+E0 机械能守恒定律 •系统中的动能和势能可以转换,各质点间的机械能 也可以互换,但保持系统的总机械能不变。 •在某一惯性系中机械能守恒,但在另一惯性系中机 械能不一定守恒。 .AN与参考系无关,而A与参考系有关
1. 明确系统及初、末状态。 2. 适用于惯性系。 Δ = 0 ⇒ + = k0pk + EEEEE p0 0,0 e = AA NI = 机械能守恒定律 3. Q ANI 与参考系无关, 而Ae与参考系有关。 •在某一惯性系中机械能守恒,但在另一惯性系中机 械能不一定守恒。 •系统中的动能和势能可以转换, 各质点间的机械能 也可以互换, 但保持系统的总机械能不变。 说明 )()( + = + − +EEEEAA p0k0pkNIe 若

A+A=(Es+Ep)-(Eko+Epo) 4.对孤立系统 若A=0,则: ANI=AE 能量转换和守恒定律 AN >0 △E>0 其他形式的能量转化为机械能。 AN<0△E<0机械能转化为其他形式的能量
4. 对孤立系统 NI = ΔEA ANI > ΔE > 0 0 0 0 ANI < ΔE < 若 则: 能量转换和守恒定律 其他形式的能量转化为机械能。 机械能转化为其他形式的能量。 )()( + = + − +EEEEAA p0k0pkNIe ,0 Ae =

[例3-12】证明流体内流速大的地方压力反而小(伯努 利方程)。 证:单位时间流过的水量相等 △V=Syt=S2V21 △V=S,△x1=2Ax2 由功能原理:(忽略高度的变化) p1S△x1-p2S2△x2 Ami 2
[例3-12] 证明流体内流速大的地方压力反而小(伯努 利方程)。 证: Δ = = 2211 tvstvsV 2211 Δ = Δ = ΔxsxsV 2 1 2 2 222111 2 1 2 1 mv mv xspxsp Δ−Δ= Δ − Δ 由功能原理:(忽略高度的变化) 单位时间流过的水量相等 v2 v1 1 Δx 2 Δx s2 s1 s2 s1 p1 p2

1△m 2 1△m2 p1-P2= 2△V 2 2△V N △m 设P= 为流体质量密度,则 △V A+2n=n+5m S p+ m2=恒量 P2 伯努利方程
2 1 2 21 2 2 1 2 1 v V m v V m pp Δ Δ − Δ Δ =− 2 2 2 2 1 1 2 1 2 1 ρ +=+ ρvpvp 2 =+ 恒量 21 ρvp 伯努利方程 s2 s1 p1 p2 设 为流体质量密度,则 V m Δ Δ ρ =