
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.5力学量算符的本征值问题 一、力学量的算符表示 这是量子力学的又一基本假设 在量子力学中,系统的任何力学量均对应一算符, 力学量所能取的值是其相应算符的本征值。例如: ·动量算符 p→p=-ihV d 对一维运动 p=-ih dx
§22.5 力学量算符的本征值问题 一、力学量的算符表示 在量子力学中,系统的任何力学量均对应一算符, 力学量所能取的值是其相应算符的本征值。例如: • 动量算符 h∇−=→r r i ˆ pp 这是量子力学的又一基本假设 对一维运动 x p d d ˆ −= ih

·坐标算符 F以下=F (就是它自己) =x ·动能算符: 2→方p=(iv)(iv)=-2v2 E= 2m 5=-2 2m 2m
• 坐标算符 rrrr r r ˆ =→ (就是它自己) ˆ = xx ( )( ) 2 22 ii ˆˆˆ hhh ∇−=∇−⋅∇−=⋅→ r r rppp • 动能算符: m p E 2 2 k = mm pp E 22 ˆˆ ˆ 22 k ∇− = ⋅ = h v v

·能量算符: E= +U( 2m 尼v2+UG) 2m ·角动量算符: 瓦=F×p j 元=×D= x y p. Py
)( 2 ˆ 2 2 rU m H h r +∇−= )( 2 2 rU m p E r r += • 能量算符: • 角动量算符: prL v r r ×= prL ˆ ˆ r r r ×= zyx ppp zyx kji ˆˆˆ r r r =
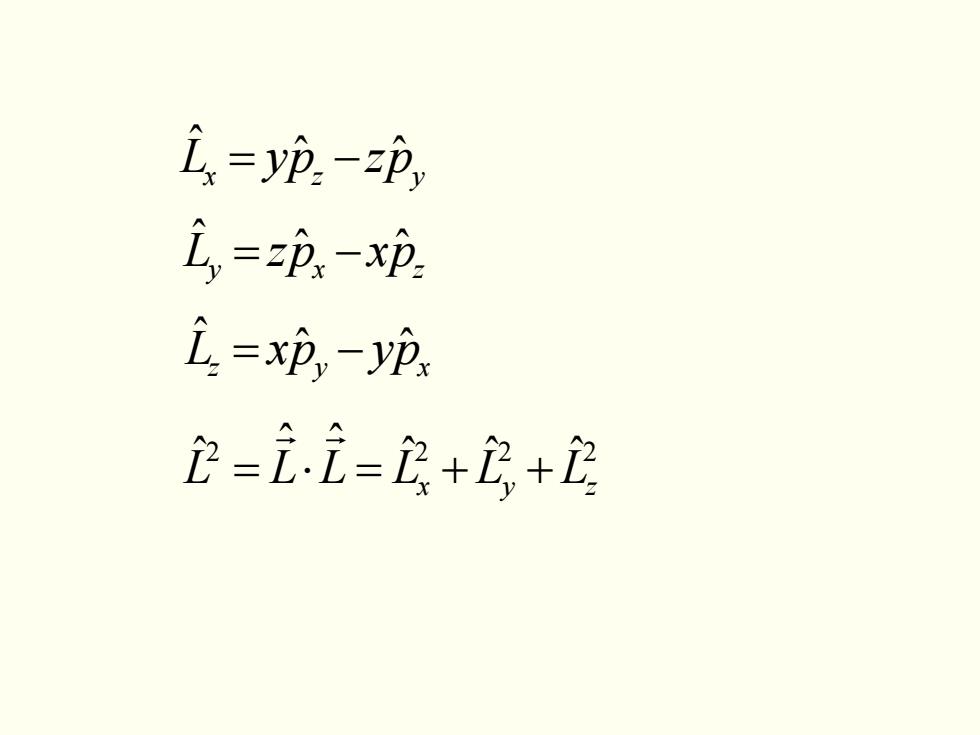
L=yp.-zp =功-p 2=x炉,-yp 企=ii=2+2+2
yzx pzpyL ˆˆ ˆ −= pxpzL zxy ˆˆ ˆ −= xyz pypxL ˆˆ ˆ −= 2 222 ˆˆˆ ˆˆ ˆ ++=⋅= LLLLLL zyx r r

二、算符的本征值问题 利用定态薛定谔方程求解能量和定态波函数实际上 是一个能量算符的本征值问题。 HΦ()=EΦ(F) 能量算符H的本征值方程 :称为能量算符的本征函数(本征态) E:称为能量算符的本征值。 为了使波函数单值、连续、有限,能量的取值受到 了限制
)()( ˆ rErH r r = ΦΦ 利用定态薛定谔方程求解能量和定态波函数实际上 是一个能量算符的本征值问题。 ——能量算符 二、算符的本征值问题 E :称为能量算符的本征值。 H ˆ 的本征值方程 为了使波函数单值、连续、有限,能量的取值受到 了限制。 r )( :称为能量算符的本征函数(本征态) r Φ

同理,通过求解动量算符、角动量算符.的本征方 程可得到相应算符的本征函数和本征值。 对于处在束缚态势场中的粒子能量只能取一系列的 分立值: E1E2...,En... END
对于处在束缚态势场中的粒子能量只能取一系列的 分立值 : E 1 , E 2 , … , En , … 同理,通过求解动量算符、角动量算符 …的本征方 程可得到相应算符的本征函数和本征值。 END