
第3章 机械能和功 §3.1功质点动能定理 §3.2保守力非保守力耗散力 §3.3质点在保守力场中的势能 §3.4质点系的势能 §3.5功能原理 能量守恒定律
第 3 章 机械能和功 §3.1 功 质点动能定理 §3.2 保守力 非保守力 耗散力 §3.3 质点在保守力场中的势能 §3.4 质点系的势能 §3.5 功能原理 能量守恒定律

§3.3质点在保守力场中的势能 一、势能的引入 与物体的位置相联系的系统能量称为势能(E,)。 保守力的功是势能变化的量度: 物体在保守力场中,b两点的势能Ea'Epb之差等 于质点由a点移动到b点过程中保守力做的功A。 E-E6=JF.d=A。 Aab=-(Epb-Epa)=-AEp >保守力的功等于系统势能的减少
一、势能的引入 与物体的位置相联系的系统能量称为势能(Ep)。 保守力的功是势能变化的量度: 物体在保守力场中a,b两点的势能Epa, Epb之差等 于质点由a点移动到b点过程中保守力做的功Aab。 ab b a ba =⋅=− ArFEE ∫ r r d pp ¾ 保守力的功等于系统势能的减少。 pp p ab = − − ab )( = −ΔEEEA §3.3 质点在保守力场中的势能
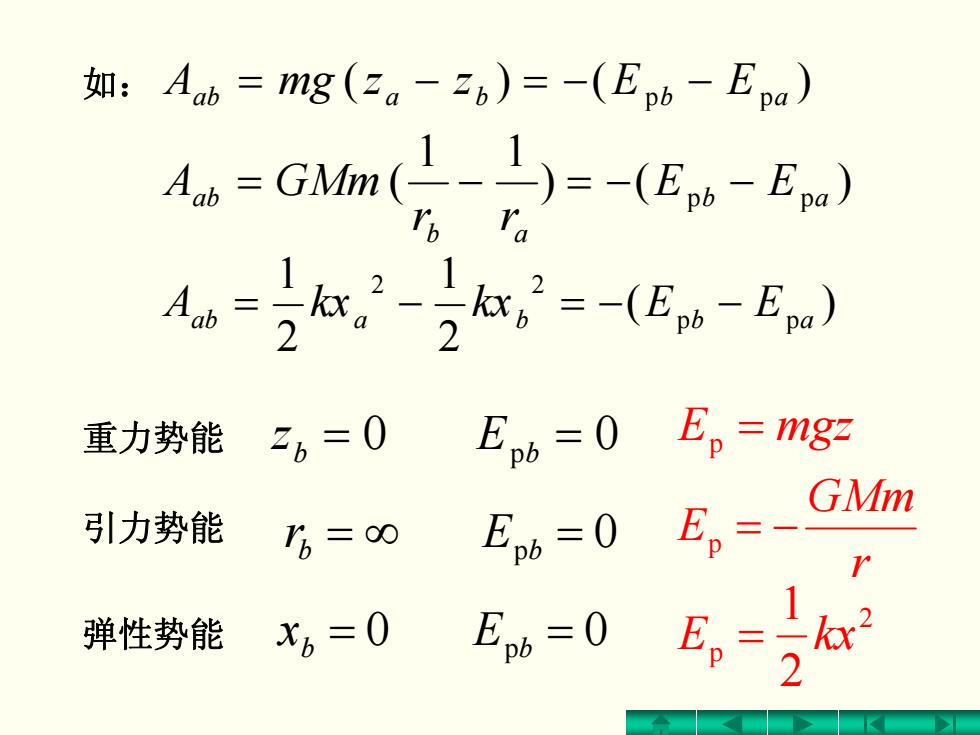
如:Aab=mg(2a-26)=-(Epb-Epa) Ab=Gm(-)=-(E6-E) Aab= ,2- 2=-(E6-Ea) 重力势能 26=0 Ep6=0 E。=mg GMm 引力势能 6=00 E6=0E。= 弹性势能 x6=0 E=0E。=5kx2
b = Ez pb = 0 0 弹性势能 重力势能 引力势能 0 b = ∞ Er pb = b = Ex pb = 0 0 p = mgzE r GMm Ep −= 2 p 2 1 = kxE )()( ab = − ba = − − EEzzmgA pp ab )( 21 21 pp 2 2 ab a b −−=−= EEkxkxA ab )() 11( pp ab ab ab EE rr = GMmA −−=− 如:

说明 ·势能是相互作用有保守力的系统的属性。 ·势能的大小只有相对的意义,相对于势能零点而 言。势能零点可以任意选取。 设空间点为势能零点,则空间任意一点下的势能为: E,()=E,()-E,()=F.d >空间某点的势能E,在数值上等于质点从该点移动到势 能零点时保守力作的功
∫ ⋅=−= 0 d)()()(p p 0p rr rFrErErE r r r r r r r ¾ 空间某点的势能Ep在数值上等于质点从该点移动到势 能零点时保守力作的功。 • 势能的大小只有相对的意义,相对于势能零点而 言。势能零点可以任意选取。 • 势能是相互作用有保守力的系统的属性。 说明 设空间 点为 r0 势能零点,则空间任意一点 的势能为: r rr
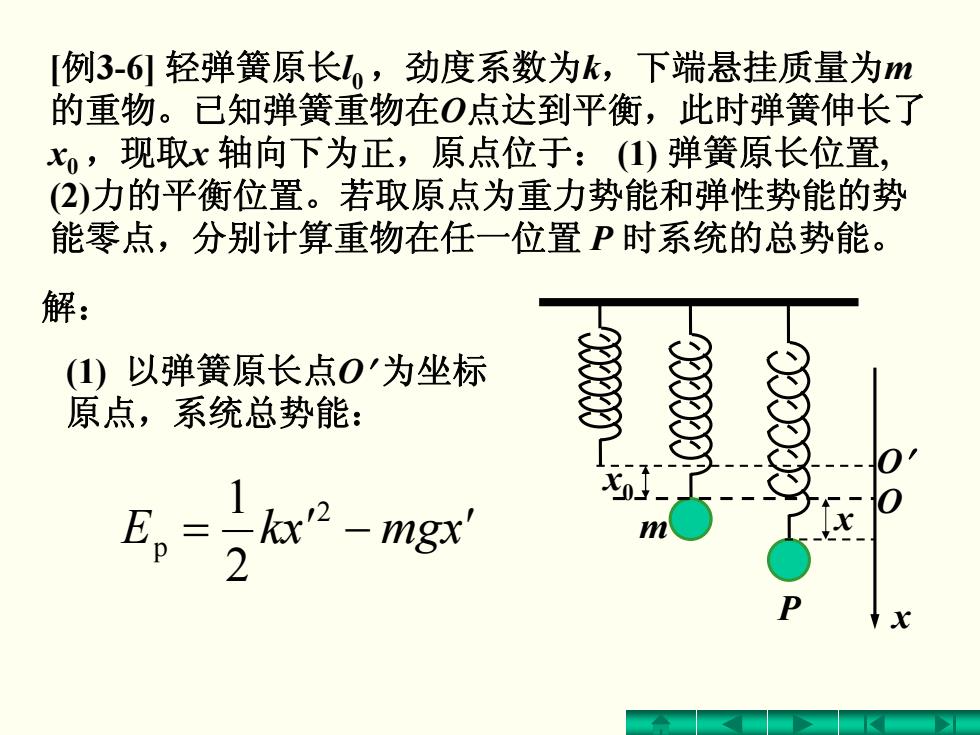
[例3-6轻弹簧原长L,劲度系数为k,下端悬挂质量为m 的重物。已知弹簧重物在O点达到平衡,此时弹簧伸长了 x,现取x轴向下为正,原点位于:()弹簧原长位置, (2)力的平衡位置。若取原点为重力势能和弹性势能的势 能零点,分别计算重物在任一位置P时系统的总势能。 解: (1)以弹簧原长点0'为坐标 原点,系统总势能:
[例3-6] 轻弹簧原长l0 ,劲度系数为k,下端悬挂质量为m 的重物。已知弹簧重物在O点达到平衡,此时弹簧伸长了 x0,现取x 轴向下为正,原点位于: (1) 弹簧原长位置, (2)力的平衡位置。若取原点为重力势能和弹性势能的势 能零点,分别计算重物在任一位置 P 时系统的总势能。 解: (1) 以弹簧原长点O′ 为坐标 原点,系统总势能: = ′ − xmgxkE ′ 2 p 21 x m O′ O P x0 x
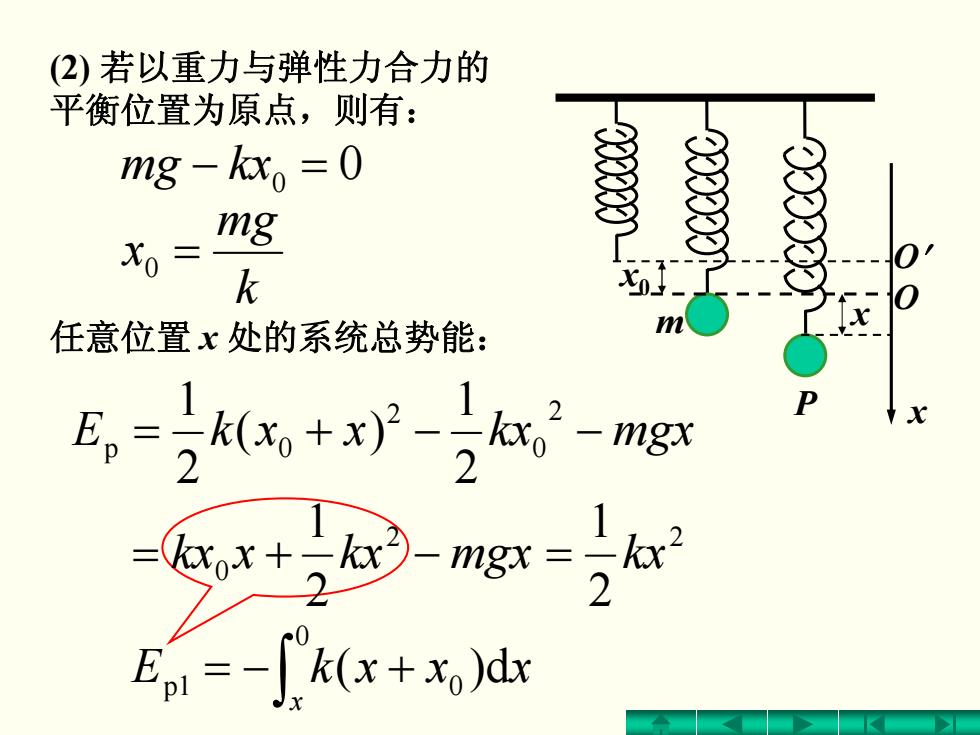
(2)若以重力与弹性力合力的 平衡位置为原点,则有: mg-kxo=0 mg X0= k 任意位置x处的系统总势能: E,=(+xP- mgx 2 =cx+2ac⊙- Ep=-k(x+xo)dx
(2) 若以重力与弹性力合力的 平衡位置为原点,则有: 任意位置 x 处的系统总势能: − kxmg 0 = 0 k mg x 0 = ∫ +−= 0 1p 0 d)( x xxxkE −−+= mgxkxxxkE 2 0 2 p 0 2 1 )( 2 1 x m O ′ O P x 0 x −+= mgxkxxkx 2 0 2 1 2 2 1 = kx

二、保守力与势能的关系 1.积分关系 E。=F(d 2.微分关系 d4=-dEp dA=F.dr=Fdx+F,dy+F.dz dE。= OE dy OE,de 8x F F.= Ep 8x y 02
二、保守力与势能的关系 1. 积分关系 2. 微分关系 = −dd EA p x y ++=⋅= zddddd zFyFxFrFA v v z z E y y E x x E E dddd p p p p ∂ ∂ + ∂ ∂ + ∂ ∂ = , p x E Fx ∂ ∂ −= , p y E Fy ∂ ∂ −= z E Fz ∂ ∂ −= p ∫ ⋅= p 0 p p d)( rrFE r r r

矢量式: ax V=i 8+j 称梯度算子。 y 0z
⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ + ∂∂ + ∂∂ −= k zE j yE i xE Fr rr r p p p Ep 矢量式: = −∇ z k y j x i ∂ ∂ + ∂ ∂ + ∂ ∂ =∇ r r r 称梯度算子

[例3-7]已知势能函数,求保守力。 (1)E。=mg2(2)E。= GMm const. 解: -=是+e= 万,=一VE。利用梯度算子在球坐标系中的表达式得:
mgz z k y j x iEF ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ −=−∇= r rr r 1 p )1( p = mgzE [ 例3-7] 已知势能函数, 求保守力。 )2( const. p +−= r GMm E 2 −∇= EF p r 解: kmg r −= )( 1 sin 1 r GMm r e r e r e r − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ −= φθφ θ φ rr r r e r GMm r 2 −= 利用梯度算子在球坐标系中的表达式得:

三、势能曲线 0 7 0 重力势能曲线 引力势能曲线 弹性势能曲线 双原子分子的势能曲线:F()= dE >0 dr r=片 dE E F()= =0 363 dr r=r 0 F()= dE 0时,物体可以在片到无穷远间运动, E。=E2<0时,物体可以在5到5间运动
三、势能曲线 o z Ep 重力势能曲线 双原子分子的势能曲线: O r Ep E1 E2 r1 2r 0r 3r ⋅ 0 d d )( 1 1 ⎟ > ⎠⎞ ⎜⎝⎛ −= =rr rE rF 0 , EE 1p >= 时, 物体可以在 r1到无穷远间运动 0 d d )( 0 0 ⎟ = ⎠⎞ ⎜⎝⎛ −= =rr rE rF 0 d d )( 3 3 ⎟ < ⎠⎞ ⎜⎝⎛ −= =rr rE rF Ep o r EE 2p <= 0时,物体可以在 到rr 32 间运动。 引力势能曲线 o x Ep 弹性势能曲线