
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振

§6.3微振动的简谐近似 如图所示,一刚体绕过o的垂直于纸面。 的轴转动,满足转动定律: d20 -mgr.sin=J dt2 式中负号表示重力矩方向恰与 角0的正方向相反。 d20 令: 02=8 得: dt2 +@2sin0=0
x o rc θ c 2 2 c d d sin t mgr J θ − θ = 式中负号表示重力矩方向恰与 角 的正方向相反。 θ 令: J mgr 2 c ω = 得: 0sin dd 2 2 2 θω =+ θt §6.3 微振动的简谐近似 如图所示,一刚体绕过o的垂直于纸面 的轴转动,满足转动定律:

由:sin0=0- 83 85 31 5! 由于0很小,略去03以上各项,则sin0≈0 d20 +o2sin0=0◆ dr2 解为: 0=0 cos(@t+p) 相应的角频率: mgre @=\J
−+−= L !5!3 sin 53 θθ 由: θθ 由于θ 很小,略去θ 3以上各项,则sinθ ≈ θ 0sin d d 2 2 2 θω =+ θ t 0 d d 2 2 2 θω =+ θ t 解为: )cos( θ =θ 0 ωt +ϕ 相应的角频率: J mgrc ω =

或从机械能守恒: Er←ner0-cos0n 两边对时间t求一阶导数: d0d20 do +mgre dt .sin8=0 dt dt2 比 d20 ,mge0=0 dt2 J 解为: 0=0 cos(ot+p)
或从机械能守恒: )cos1() dd( 21 c 2 θ θ = mgr −+ t JE 解为: )cos( θ =θ 0 ωt +ϕ x o rc θ c 0sin d d d d d d 2 c 2 θ =⋅+⋅ θθθ t mgr tt J 0 d d c 2 2 θ =+ θ J mgr t 两边对时间 t 求一阶导数:

[例题6-1一质点沿x轴作简谐振动,振幅为12cm,周期为2s。 当仁0时,位移为6cm,且向x轴正方向运动。求:1.振动式。 2.仁0.5s时,质点的位置、速度和加速度。3.如果在某时刻 质点位于x=-6cm,且向x轴负方向运动,求从该位置回到平 衡位置所需要的时间。 解:设简谐振动表达式为x=Ac0S(Ot+p) (rad/s) 2π 已知:A=12cm,T=2s,0= x=0.12c0s(πt+p) 初始条件: t=0时,x=0.06m,v>0
[例题6-1] 一质点沿x轴作简谐振动,振幅为12cm,周期为2s。 当t=0时, 位移为6cm,且向x轴正方向运动。求:1. 振动式。 2. t=0.5s时,质点的位置、速度和加速度。3. 如果在某时刻 质点位于x=-6cm,且向x轴负方向运动,求从该位置回到平 衡位置所需要的时间。 解: 设简谐振动表达式为 已知: A=12cm , T=2s , π )s/rad( 2π == T ω 初始条件: t = 0 时, x0 = 0.06m , v0 > 0 = ω tAx +ϕ )cos( x = cos(12.0 πt +ϕ )
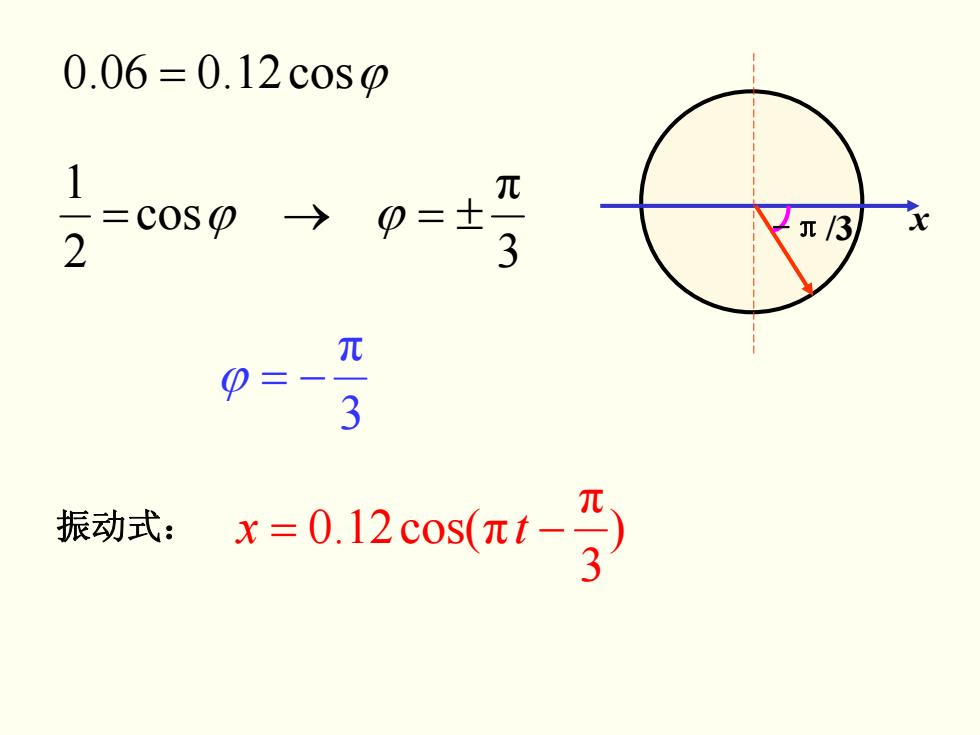
0.06=0.12c0s0 1 =coS →0=士 3 13 2 元 3 振动式:X=0.12c0s(1-孕
3 π cos 2 1 ϕϕ ±=→= 3 π ϕ −= 振动式: ) 3π x = cos(12.0 πt − x -π/3 = cos12.006.0 ϕ
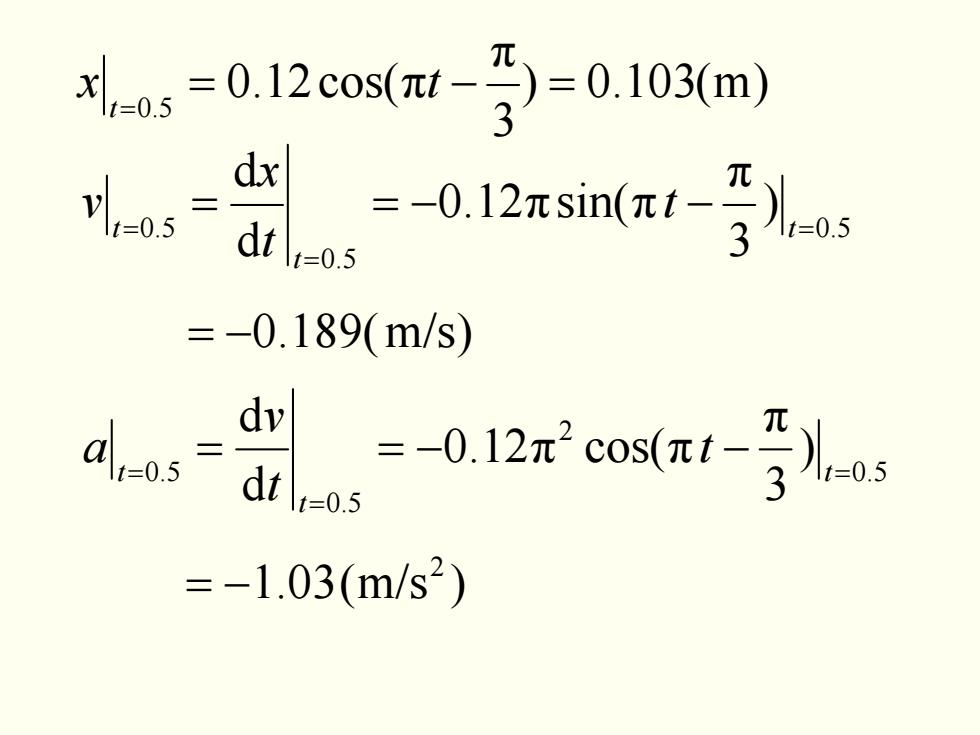
40s=0.12co8(t-3)=0.103(m) dx 5= dt =-0.12xsinπt-牙Xag t=0.5 =-0.189(m/s) dv t=0.5 0.12 cos( =-1.03(m/s2)
5.0 5.0 5.0 ) 3π 12.0 πsin(π dd = = = −== − t t t t t x v 5.0 2 5.0 5.0 ) 3π 12.0 π cos(π dd = = = −== − t t t t t v a )m(103.0) 3π cos(12.0 π 5.0 = =− = x t t −= )m/s(189.0 )m/s(03.1 2 −=

设在某一时刻t1,x=-0.06m 代入振动式 :-0.06=0.12c0s(πt1-π/3) c0s(πt-π3)=2 元 2元 4元 元t 或 3 3 2元 2元 πt1 >t1=1s 3 3
设在某一时刻 t1, x = -0.06 m 代入振动式: − = (cos12.006.0 t1 − ππ )3 2 1 (cos ππ )3 t1 −=− 3 4π 3 2π 3 π πt1 =− 或 s1 3 2π 3 π πt1 t1 =→=− -π/3 x 2π 3/

元 3元 1 元t2 t2= S) 3 2 2π/3
s)( 611 23π 3π πt2 t2 =→=− )s( 65 1 611 ttt 12 =−=−=Δ -π/3 x 2π 3/

「例题6-21两质点作同方向、同频率的简谐振动,振幅相等。 当质点1在x=A/2处,且向左运动时,另一个质点2在x2= A/2处,且向右运动。求这两个质点的相位差。 解: -A -A/2 0 A/2 A x=Acos(@t+) A/2=Ac0s(0t+p1)→0t+91=±π/3 0t+9,=/3 π3
[例题6-2] 两质点作同方向、同频率的简谐振动,振幅相等。 当质点1在 x1=A/2 处,且向左运动时,另一个质点2在 x2= - A/2 处,且向右运动。求这两个质点的相位差。 )(cos 1 = ω +ϕ1 tAx = ω tAA +ϕ1 )(cos2 →ωt +ϕ1 = ± π 3 ωt +ϕ1 = π 3 解: -A o A -A/2 A/2 x π/3