
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振

§6.7受迫振动 共振 一、受迫振动 受迫振动:系统在周期性的外力持续作用下所 发生的振动。 策动力: 周期性的外力。 设: F=Fo cos@t
系统在周期性的外力持续作用下所 发生的振动。 受迫振动: 策动力: 周期性的外力。 设: = 0 cos ωtFF 一、受迫振动 §6.7 受迫振动 共振 Fr r xkf v v F −= o x x

d2x dx m =-kx-Y dt +Fcosωt 令: k 2 Y=26 m m d2x dx +2δ +00x=0 cos wt dt2 dt
tF t x kx t x m γ cosω d d d d 2 0 2 +−−= 令: δ γ ω 2 20 == mm k t m F x t x t x ωδ cosω d d 2 d d 2 0 2 0 2 =++

x=Ae 5 cos(-t+)+Acos(@t+p) 稳定振动状态: x=Acos(@t+o) A= F tan⑩= k 2 k 0n- om- 0 >结论:在稳定振动状态下,受迫振动的频率等于 策动力的频率
cos( )cos() 0 22 0 0 ϕωϕδω δ = +++− − eAx tAt t 稳定振动状态: = ω tAx +ϕ )cos( 2 2 0 ⎟⎠⎞ ⎜⎝⎛ −+ = ω ωγω k m F A ω ω γ ϕ k m − tan = 在稳定振动状态下,受迫振动的频率等于 策动力的频率。 ¾结论:

在稳态时,振动物体的速度 dx V= dt =mcosoM+g+3 其中: F max +(cm-k
在稳态时,振动物体的速度 ) 2 π cos( d d == max tv ϕω ++ t x v 其中: 2 2 0 max )( ω ωγ k m F v −+ =
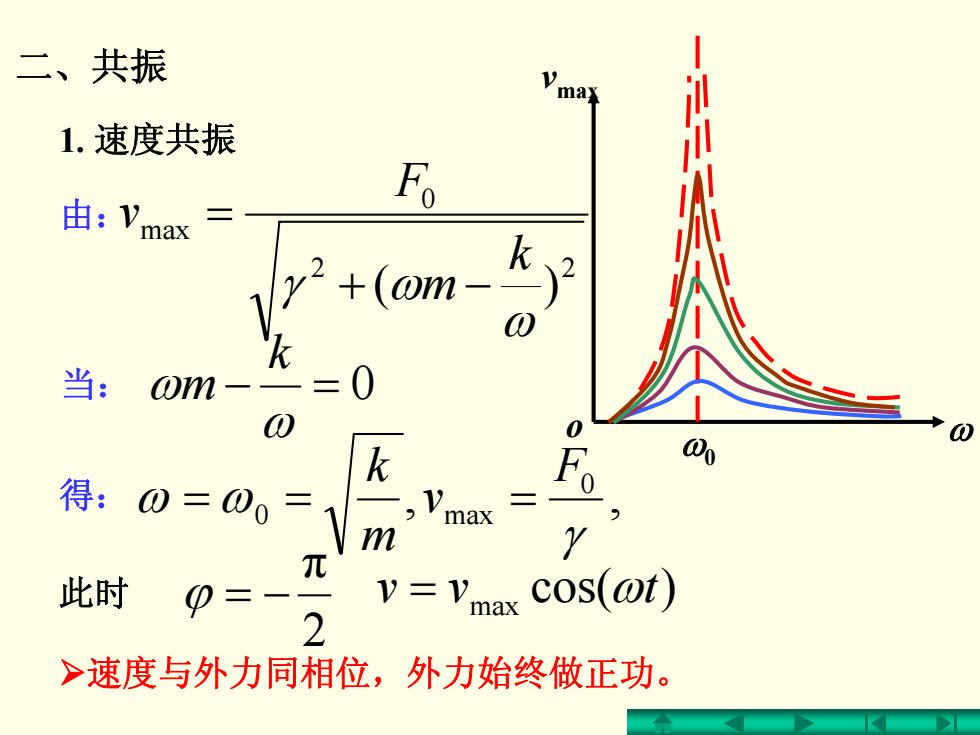
二、共振 max 1.速度共振 F 由: 二 max y2+(om- k 2 0 当: om- 一 =0 O 0 k 00 得: 0 =00 V max m Y 元 此时 V=Vmax cos(@t) 2 >速度与外力同相位,外力始终做正功
二、共振 1. 速度共振 由: 2 2 0 max )( ω ωγ k m F v −+ = 当: =− 0 ω ω k m 得: ,, 0 0 max γ ωω F v m k == = 此时 2 π ϕ −= )cos( max = ωtvv ¾速度与外力同相位,外力始终做正功。 vmax o ω ω0

2.位移共振 共振:当策动力的频率接近于固有频率时,受迫振动 的振幅达到最大值的现象。 由: F A= 令: d4=0,得:0=v02-262=0, d F A ax 2m8Vo,2-6
2. 位移共振 共振:当策动力的频率接近于固有频率时,受迫振动 的振幅达到最大值的现象。 2 2 0 ⎟⎠⎞ ⎜⎝⎛ −+ = ω ωγω k m F 由: A 2 2 0 0 max 2 −δωδ = m F A 令: r 2 2 0 ,0 2 dd ωδωω ω= =−= A 得:

0,-V,2-262 A : F。 Amax 阻尼=0 2mδV,2-2 阻尼较小 >结论: 阻尼较大 阻尼系数6越小, 共振角频率ω越接近于 000 系统的固有频率o,,同 时共振振幅A也越大。 END
阻尼系数δ 越小, 共振角频率ωr越接近于 系统的固有频率ω0 ,同 时共振振幅Ar也越大。 ¾结论: 2 2 r 0 −= 2δωω 2 2 0 0 max 2 −δωδ = m F A o A ωrω0 ω 阻尼=0 阻尼较小 阻尼较大 END