
第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量
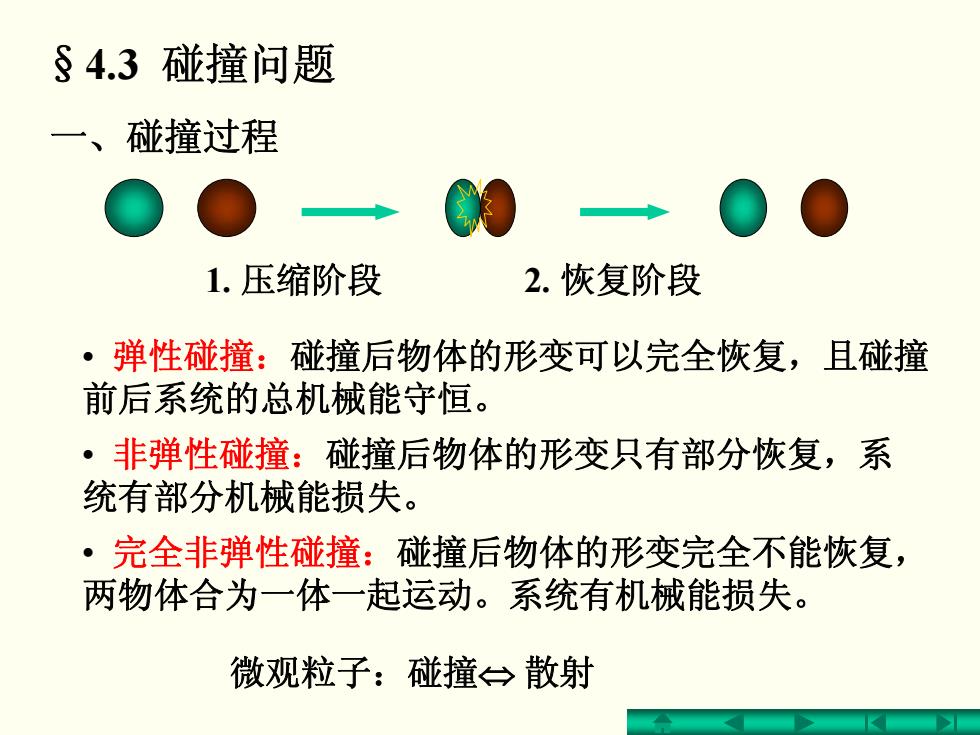
§4.3碰撞问题 一、碰撞过程 1.压缩阶段 2.恢复阶段 ·弹性碰撞:碰撞后物体的形变可以完全恢复,且碰撞 前后系统的总机械能守恒。 ·非弹性碰撞:碰撞后物体的形变只有部分恢复,系 统有部分机械能损失。 ·完全非弹性碰撞:碰撞后物体的形变完全不能恢复, 两物体合为一体一起运动。系统有机械能损失。 微观粒子:碰撞→散射
一、碰撞过程 1. 压缩阶段 2. 恢复阶段 §4.3 碰撞问题 微观粒子:碰撞⇔ 散射 • 弹性碰撞:碰撞后物体的形变可以完全恢复,且碰撞 前后系统的总机械能守恒。 • 非弹性碰撞:碰撞后物体的形变只有部分恢复,系 统有部分机械能损失。 • 完全非弹性碰撞:碰撞后物体的形变完全不能恢复, 两物体合为一体一起运动。系统有机械能损失

(1)弹性碰撞 动量守恒:m1y1o+m2'20=mV1+m2V2 12 1 动能守恒: ,21 2 mio+ 2 n.120-o11'1t_ 2 2 一→y=例-m,+2m2 m +m V2-y1=y10-V20 v,(ms-m xn+2mvo m+m V10 1V20
(1) 弹性碰撞 v 2 v 1 v20 v10 2211202101 动量守恒: + = + vmvmvmvm 动能守恒: 2 22 2 11 2 202 2 101 2 1 2 1 2 1 2 1 +=+ vmvmvmvm ( ) 21 1021 202 1 2 mm vmvmm v + − + = ( ) 21 2012 101 2 2 mm vmvmm v + − + = 201012 − = − vvvv

讨论1.当m,=m,时,则:1=V20V2=V10 在一维弹性碰撞中,质量相等的两个质点在碰撞中交 换彼此的速度。 2.若20=0,且m>m1,则:1≈-10y2≈0 质量很小的质点与质量很大的静止质点碰撞后,调转运动 方向,而质量很大的质点几乎保持不动。 3.若o0,且m<m,则:y1≈Y10V2≈2Y10 质量很大的入射质点与质量很小的静止质点碰撞后速度几 乎不变,但质量很小的质点却以近两倍的速度运动起来。 (m-m2)y1o+2m2y20 (m2-m1)y20+2my10 m1+m2 m1+m2
1. 当m1=m2时, 则: 102201 讨论 = = vvvv 在一维弹性碰撞中, 质量相等的两个质点在碰撞中交 换彼此的速度。 2. 若v20=0,且 m2>>m1,则: ( ) 21 1021 202 1 2 mm vmvmm v + − + = ( ) 21 2012 101 2 2 mm vmvmm v + − + = −≈ vvv 2101 ≈ 0 质量很小的质点与质量很大的静止质点碰撞后,调转运动 方向,而质量很大的质点几乎保持不动。 3. 若v20=0, 且m2<<m1, 则: 2 102101 ≈ ≈ vvvv 质量很大的入射质点与质量很小的静止质点碰撞后速度几 乎不变,但质量很小的质点却以近两倍的速度运动起来

(2)完全非弹性碰撞 动量守恒: mivio m2v2o (m +m2 )v V= mV10+m2y20 m1+m2 机械能损失: AE=R-Ew=m+m2-(5m哈+ m2V20 AE=、 m,m(y10-y20))月 2(m1+m2) V10 1V20
(2) 完全非弹性碰撞 动量守恒: + 202101 = + 21 )( vmmvmvm 21 202101 mm vmvm v + + = 机械能损失: ) 21 21()( 21 2202 2101 2 0kk 21 +−+=−=Δ vmvmvmmEEE )(2 )( 21 2 201021 mm vvmm E + − −=Δ v v20 v10

(3)非弹性碰撞: 动量守恒:my10+n2V2o=my1+m2V2 碰撞定律:碰撞后两球的分离速度(y,-)与碰撞前两 球的接近速度(y0y20)成正比。比值由两球 的质料决定。 V2-y1 e= 恢复系数 y10-V20 V10 V20
动量守恒: 2211202101 vmvmvmvm (3) 非弹性碰撞: + = + 碰撞定律: 碰撞后两球的分离速度(v2-v1)与碰撞前两 球的接近速度(v10-v20) 成正比。比值由两球 的质料决定。 2010 12 vv vv e − − = ——恢复系数 v2 v1 v20 v10

弹性碰撞:e=1 (y2-y1)=(y10V20〉 V2-1 e= 非弹性碰撞:0<e<1 V10-V20 完全非弹性碰撞:e=0 '2=V1 碰后两球的速度: (1+e)(y10-V20) y1=V10-m2 mm (1+e)(y1o-v2o) V2=V20+m1 m1+m2 机械能损失: -e
碰后两球的速度: 21 2010 2101 ))(1( mm vve mvv + + − −= 21 2010 1202 ))(1( mm vve mvv + + − += 机械能损失: 2 2010 21 2 21 k )()1( 2 1 vv mm mm E e − + −−=Δ 完全非弹性碰撞: e = 0 v 2=v 1 非弹性碰撞: 0 < e < 1 弹性碰撞: e = 1 ( v 2-v 1 )= ( v10-v20 ) 2010 12 vv vv e − − =

[例4-8)已知板M,L;小球m,vo,h。弹簧k,桌面光 滑,掉下时与板为弹性碰撞。求()弹簧最大压缩量,(2) 若只发生一次碰撞,则y应满足什么条件? 解:(1)碰撞时(y方向碰撞), m vo 小球速度为: Vx Yo,Vy =v2gh 设'为小球与平板碰撞后的速 度,V为平板碰撞后的速度。对 于弹性碰撞: my,mv,MV 2mk,2+n,)=2mlc.+y+5Mw
[例4-8] 已知板 M,l;小球 m, v0 , h。弹簧 k,桌面光 滑,掉下时与板为弹性碰撞。求(1) 弹簧最大压缩量, (2) 若只发生一次碰撞,则v0 应满足什么条件? 解: ghvvvx y 2, 0 == MVvmmv = ′yy + ( ) ( ) 22 22 2 21 21 21 yx +=+ ′yx + MVvvmvvm (1)碰撞时(y方向碰撞), 小球速度为: h l m v0 x k y 设 为小球与平板碰撞后的速 度, 为平板碰撞后的速度。对 于弹性碰撞: V r v' r

解得:V- 2m2gh M-m2gh m+M =- m+M 碰后,板、弹簧、地球系统: n2+y-方a+4-gy 其中△y= Mg k 得: 2m 2Mgh △y=k m+M\k
解得: Mm ghm V + = 22 Mm ghmM vy + − ′ −= 2 碰后,板、弹簧、地球系统: ( ) Δ−Δ+Δ=Δ+ yMgyykykMV 2 0 20 2 21 21 21 得: k Mgh Mm m V k M y 22 + ==Δ k Mg 其中 y0 =Δ

(2)小球从桌面下落至板上经历的时间: =2h/g 球要与板发生碰撞,首先 须满足条件1: V41≤1 一 次碰撞后,小球弹起再落 回原碰撞处经历的时间: 3 6=2 8
(2)小球从桌面下落至板上经历的时间: /2 ght1 = 球要与板发生碰撞, 首先 须满足条件 1: ≤ ltv 10 一次碰撞后,小球弹起再落 回原碰撞处经历的时间: g v t y ′ = 2 2 h l m v0 k