
第14章稳恒磁场 §14.1磁感应强度 及洛仑滋力公式 §14.2毕奥一萨伐尔定律 §14.3磁高斯定理安培环路定理 §14.4磁场对载流导线的作用 §14.5带电粒子的运动
第 14 章 稳恒磁场 §14.1 磁感应强度 及洛仑兹力公式 §14.3 磁高斯定理 安培环路定理 §14.2 毕奥—萨伐尔定律 §14.4 磁场对载流导线的作用 §14.5 带电粒子的运动

§14.4磁场对载流导线的作用 一、安培力公式 B 一个载流子受力: Idi R=g×B 一个电流元受力: n gl dF=nSdl(qvx B) .j=nqw1=Sdl∥j →dF=Sdlj×B)=Id×B八d F=∫dF=J(di×B周) a
§14.4 磁场对载流导线的作用 一、安培力公式 一个载流子受力: BvqF r r r L ×= BvqlnSF )(dd r r r ×= vnqj r r Q = = SjI j//l r r d BlIBjlSF r r r r r d)(dd ×=×=⇒ ∫∫ ×== l l BlIFF )d(d r r r r 一个电流元受力:

[例14-9]如图所示,求导线受力? 解: dF2 =B I,dl, 单位长度 2=B1=4L d Id7 12d0 受力: dl 2πa d近 B.1 =Eol1l2 dl, 2元a 1A是如何定义的? 2x10-7NWm=,×1x1A'/m 2元×1 同时确定:4=4π×10-7N/A2
d d 2212 = lIBF 单位长度 受力: a II IB l F d 2π d 210 12 1 1 μ == a II IB l F d 2π d 210 21 2 2 μ == 1A是如何定义的? /mA 2π 1 11 N/m102 7 0 2 × × × × = − μ 27 0 4 π N/A10− 同时确定:μ ×= d 11 lI r d 22 lI r 1 I dF1 r dF2 r a 2 I [例14-9] 如图所示,求导线受力 ? 解:

[例14-10]求匀强磁场中载流导线受力。 解:F=-(6×8 =(d)×B X XX XXX =IAB×B 在均匀磁场中,和AB段直电流受力相同!
∫ ×= l BlIF )d( r r r BlI l r r ×= ∫ )d( [例14-10] 求匀强磁场中载流导线受力。 A B I AB B r = × 解: 在均匀磁场中,和 AB 段直电流受力相同!
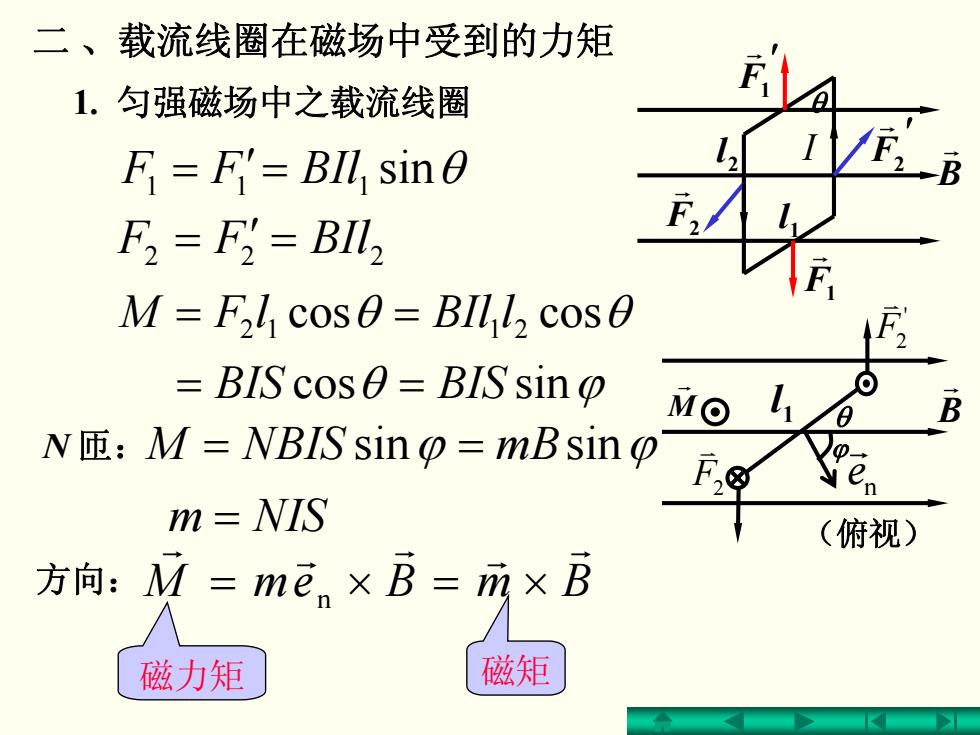
二、载流线圈在磁场中受到的力矩 1.匀强磁场中之载流线圈 A F=F'=BIL sin0 F2=F;=BIL, M=Fh cos=BIl l,cos BIS cos0=BIS sino B N匝:M=VBIS sin=mBsinp m NIS (俯视) 方向:M=men×B=m×B 磁力矩 磁矩
二 、载流线圈在磁场中受到的力矩 1. 匀强磁场中之载流线圈 = ′ = BIlFF 111 sin θ 22 = BIlFF 2 = ′ θ ϕ θ θ cos sin cos cos 12 21 BIS BIS lFM lBIl = = = = N 匝: NISm NBISM mB = = sin ϕ = sin ϕ 方向: BmBemM r r r r r n ×=×= 磁力矩 磁矩 θ F1 r ′ F1 r F2 r ′ F2 r 1 l 2 l B I r n e ϕr B r M θ r (俯视) 1 l F2 v ' F2 v

2.匀强磁场中之任意形状平面载流线圈 F=f(dl×B)=1(fd)×B=0 小矩形:dM=dm×Bdm=IdSe。 总力矩:=∫dM=∫(dmxB)=dm)×B =(1dSe)xB=Ie×B∫ds =ISen×B=m×B
2. 匀强磁场中之任意形状平面载流线圈 =×=×= 0)d()d( ∫∫ BlIBlIF l l r r r r r 小矩形: dd dd n eSImBmM 总力矩: r r r r r =×= BmBmMM r r r r r r ×=×== ∫ ∫ ∫ )d()d(d ∫ ∫ ×=×= d )d( SBeIBeSI n n r r r r BmBeIS r r r r n ×=×=

三、磁力之功 1.运动之载流导线 F=BIl A=F△x=BIlx =BI△S=I△Φ m =I(Φ-Φ) △少m:扫过的磁通量或磁通之增量
三、磁力之功 = BIlF = Δ = ΔxBIlxFA ΔΦ m:扫过的磁通量或磁通之增量 ΔΔ Φ m = = ISBI )( = Φ −Φ if I 1. 运动之载流导线

2.转动之载流线圈 M=m×B do不e M=ISBsin o 转动d0 ?? d4=-BIS sin pdo .do>0,dA<0 dA=IBSd(coso)=Id(BS cosp)=Idp
2. 转动之载流线圈 BmM r r r ×= = ISBM sinϕ d = −BISA ϕdsin ϕ ??? Q ϕ > A < 0d ,0d ϕ ϕ d)cos(d)(cosdd Φ m = IBSA = BSI = I 转动 dϕ dϕ

p1→p2 BIS sin odo_ =I△Φm=I(Φm,-Φm)=I(Φ-功) 电流与外磁场呈右手螺旋关系磁通量取正,反之取负。 dA=-BIS sin pdo do>0,dA<0 dA=IBSd(cosp)=Id(BS cosp)=IdPm
ϕ →ϕ 21 ∫ −= 21 dsin ϕϕ BISA ϕϕ Δ )( m m2 m1 = Φ = II Φ − Φ 电流与外磁场呈右手螺旋关系磁通量取正,反之取负。 dϕ d = −BISA ϕdsin ϕ Q ϕ > A < 0d ,0d ϕ ϕ d)cos(d)(cosdd Φ m = IBSA = BSI = I ∫ = m2 m1 d m ΦΦ I Φ )( = Φ −Φif I
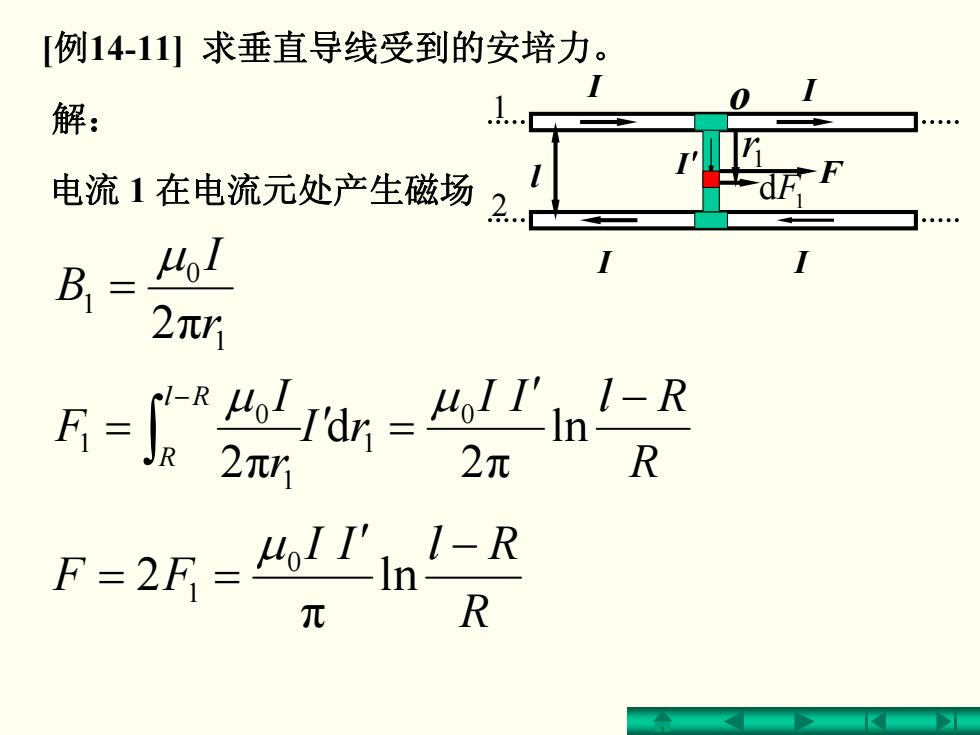
[例14-11)求垂直导线受到的安培力。 解: 电流1在电流元处产生磁场2 B= 41 2元r -”- I-R -In 2Tr 2兀 R F=25=MIn-R 元
1 0 1 2πr I B μ = F 1rdF1 [例14-11] 求垂直导线受到的安培力。 l I I I I I′ 1 2 o R II Rl rI r I F Rl R ′ − = ′ = ∫ − ln 2π d 2π 0 1 1 0 1 μ μ R II Rl FF ′ − == ln π 2 0 1 μ 解: 电流 1 在电流元处产生磁场