
第13章电介质 §13.1静电场中的电介质 §13.2介质中的高斯定理 §13.3介质边界两侧的静电场 §13.4静电场的能量
第 13 章 电介质 §13.2 介质中的高斯定理 介质中的高斯定理 §13.1 静电场中的电介质 静电场中的电介质 §13.4 静电场的能量 §13.3 介质边界两侧的静电场 介质边界两侧的静电场
§13.4静电场的能量 一、带电体系的静电能 若点电荷q0处于q的电场中, 静电能为: W.=4'=464元er 9 dr ◆把qo从P点移到无限远时 静电场力作的功,就是 ·d “系统”的静电势能。 或:把qo从无限远移动到P点的过 V=E.dF 程中,外力反抗静电力作的功
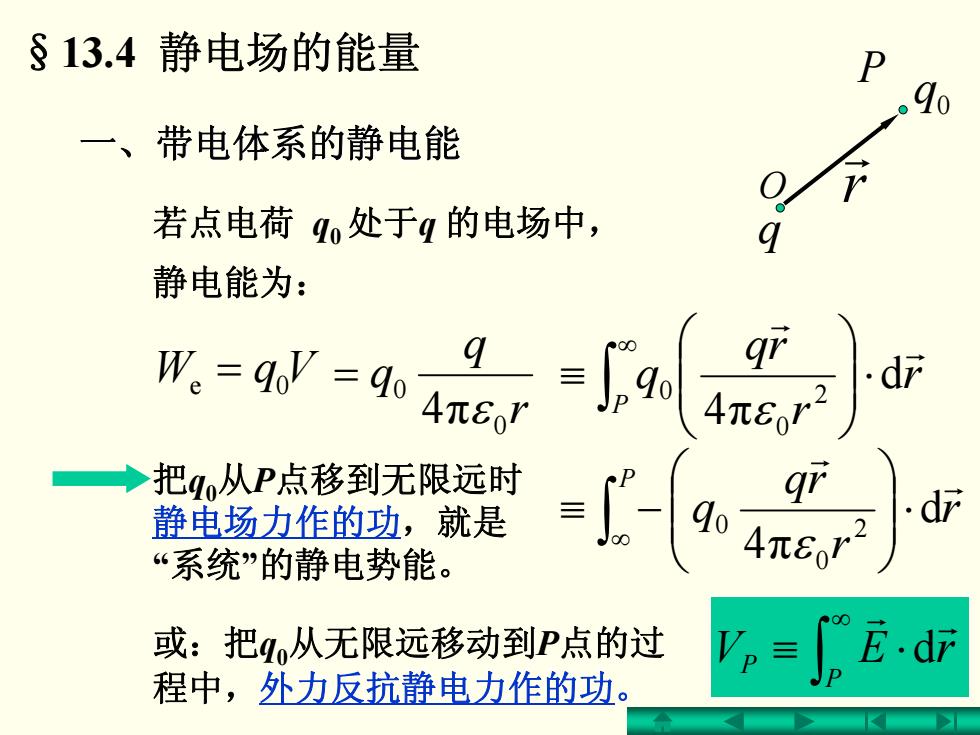
一、带电体系的静电能 带电体系的静电能 若点电荷 q0 处于q 的电场中, = 0e VqW 静电能为: §13.4 静电场的能量 r q q 0 0 4πε = ∫∞ ⋅ ⎟⎟⎠⎞ ⎜⎜⎝⎛ ≡ P r rrq q r r d 4π 2 0 0 ε r r q 0 q P O 把q0从P点移到无限远时 静电场力作的功,就是 “系统”的静电势能。 r r rq q P r r ∫∞ ⋅ ⎟⎟⎠⎞ ⎜⎜⎝⎛ −≡ d 4π 2 0 0 ε 或:把q0从无限远移动到P点的过 程中,外力反抗静电力作的功。 ∫∞ ⋅≡ P P rEV r r d

*对于点电荷体系(或连续带电体),系统的能 量可以有类似的定义: >把点电荷体系无限分离到彼此间相距无限远的 过程中静电场力作的功,叫作该系统内的静电势 能。 >对连续带电体,可以把带电体看成是由无限多 电荷元组成的点电荷体系。这样,连续带电体的 静电能量的定义同上
¾ 把点电荷体系无限分离到彼此间相距无限远的 过程中静电场力作的功,叫作该系统内的静电势 能。 ¾ 对连续带电体,可以把带电体看成是由无限多 电荷元组成的点电荷体系。这样,连续带电体的 静电能量的定义同上。 * 对于点电荷体系(或连续带电体),系统的能 量可以有类似的定义: 量可以有类似的定义:

二、点电荷系的能量 电势能: 91 W。=q24元6r 02 二q小4元60' =qK+9] 个点电荷系统的电势能:队。=)∑9,叫 其中,V,为除4:外其它点电荷在4:处产生的电势之和
二、点电荷系的能量 二、点电荷系的能量 q 2 r q qW 0 1 2e 4 π ε = 电势能: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ +⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = r q q r q qW 0 1 2 0 2 e 1 42 π 4 π 1 ε ε n个点电荷系统的电势能: 个点电荷系统的电势能: ∑= = n i VqW ii 1 e 2 1 q1 r q 2 [ ] 2211 2 1 += VqVq r q q 0 2 1 4 π ε = q 1 其中, Vi 为除 q i 外其它点电荷在 q i处产生的电势之和。 处产生的电势之和

三、连续带电体的静电能量 体状带电体:所.=广P八(pd) 面状带电体,化.=P(GdS) 线状带电体:.=V(2d > 式中V表示电荷元处的电势,原则上不包括该电荷元的贡 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略
三、连续带电体的静电能量 三、连续带电体的静电能量 = ∫ d q τ τρ )d( 2 1 体状带电体: e VW 面状带电体: ∫ = S SVW )d( 2 1 e σ 线状带电体: ∫ = L lVW )d( 2 1 e λ ¾ 式中 V 表示电荷元处的电势,原则上不包括该电荷元的贡 表示电荷元处的电势,原则上不包括该电荷元的贡 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略。 献。但由于电荷元的贡献为一阶小量,其中的差别可以忽略

讨论与说明: 1.点电荷系的静电能是指点电荷间的相互作用能量之 和一称为“互能”。互能可能为正值也可能为负 值,由系统构成决定。 2.单个连续带电体的总静电能习惯上称为“自能”。 数值上它等于将该带电体上各个部分的电荷分散到无 限远的状态时,电场力所作的总功。自能只能为正。 3.连续带电体系的静电能等于各连续带电体的“自能”和各 连续带电体之间的“互能”之总和(总为大于零的值)
讨论与说明: 1. 点电荷系的静电能是指点电荷间的相互作用能量之 点电荷系的静电能是指点电荷间的相互作用能量之 和——称为“互能”。互能可能为正值也可能为负 互能可能为正值也可能为负 值,由系统构成决定。 由系统构成决定。 2. 单个连续带电体的总静电能习惯上称为 的总静电能习惯上称为“自能”。 数值上它等于将该带电体上各个部分的电荷分散到无 数值上它等于将该带电体上各个部分的电荷分散到无 限远的状态时,电场力所作的总功。 限远的状态时,电场力所作的总功。自能只能为正。 3. 连续带电体系的静电能等于各连续带电体的“自能”和各 连续带电体之间的“互能”之总和(总为大于零的值 总为大于零的值)
四、电容器储存的静电能量(带电±Q) dA=dq'uas=dg 9 B dq AB 电容器的静电能: )=CU W≡A
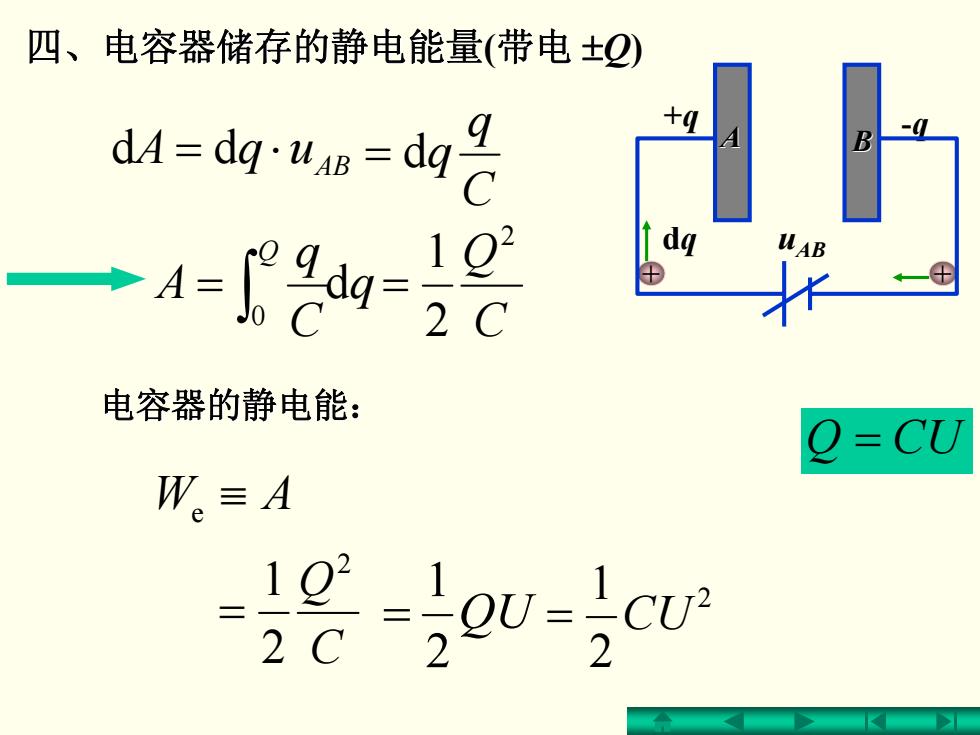
四、电容器储存的静电能量 四、电容器储存的静电能量 (带电 ± Q ) uqA AB = dd ⋅ + q - q uAB + + d q = CUQ e ≡ AW C Q 2 2 1 = 电容器的静电能: 电容器的静电能: C q = d q q C q A Q d ∫0 = C Q 2 2 1 = QU 2 1 = 2 2 1 = CU A B

五、电场的能量,能量密度 设带电系统静电作用能量是以电场能量 的形式储存在电场中的。 以平板电容器为例:W=CU2 es 其中:C U=Ed d →W。= 1 aS d (Ed) 2E'5 电容器体积:V=Sd
五、电场的能量,能量密度 五、电场的能量,能量密度 设带电系统静电作用能量是以电场能量 的形式储存在电场中的。 2 e 2 1 = CUW d S C ε = = EdU ( ) 2 e 2 1 Ed d S W ε = ( ) SdE 电容器体积:V = Sd 2 2 1 = ε 其中: 以平板电容器为例:

电场的能量密度:单位体积电场所具有的能量 We E2 2 把电场能量密度推广到非均匀场的情况! w=小edr=∫s地dr=D-a →W。= 12 d (Ed) cE(Sd) 电容器体积:V=Sd
电场的能量密度: 电场的能量密度: 单位体积电场所具有的能量 单位体积电场所具有的能量 2 e 2 1 = ε Ew ∫ = τ dτ wW e ∫ = τ dτε 21 2 E ∫ ⋅= τ dτ 21 EDr r 把电场能量密度 把电场能量密度推广到非均匀场的情况! 非均匀场的情况! ( )2 e 21 Ed dS W ε = ( ) SdE 电容器体积:V = Sd 2 21 = ε

[例题13-4求带电量为Q,半径为R的均匀球体的静电场能。 [解法一】按照电势能定义式求 利用高斯定理: E,·4元r2= 4πr3/3 4πR3/3 80 得球内电场:E,= Or 4元6R3 (r≤R) Q 同样得球外 电场: 4π8r2 (r>R) 球内一点电势:V=[E,dr+E,d w.--fv(pdr)p=R
[例题13 -4]求带电量为 Q ,半径为 R 的均匀球体的静电场能。 [解法一] 按照电势能定义式求 0 3 3 2 1 4 π 3 4 π 3 4 π ε r R Q rE =⋅ 得球内电场: )( 4 π 3 0 1 Rr R Qr E = ≤ ε 同样得球外 电场: )( 4 π 2 0 2 Rr r Q E = > ε ∫∫ ∞ += R R r 1 2dd rErEV 4 π 3 3 R Q ρ = 球内一点电势: ∫ = τ τρ )d( 2 1 e VW 利用高斯定理: R Q r