
第1章质点运动学 §1.1基本概念 §1.2质点的位移和速度 §1.3质点的加速度 §1.4相对运动
第 1 章 质点运动学 §1.1 基本概念 §1.2 质点的位移和速度 §1.3 质点的加速度 §1.4 相对运动
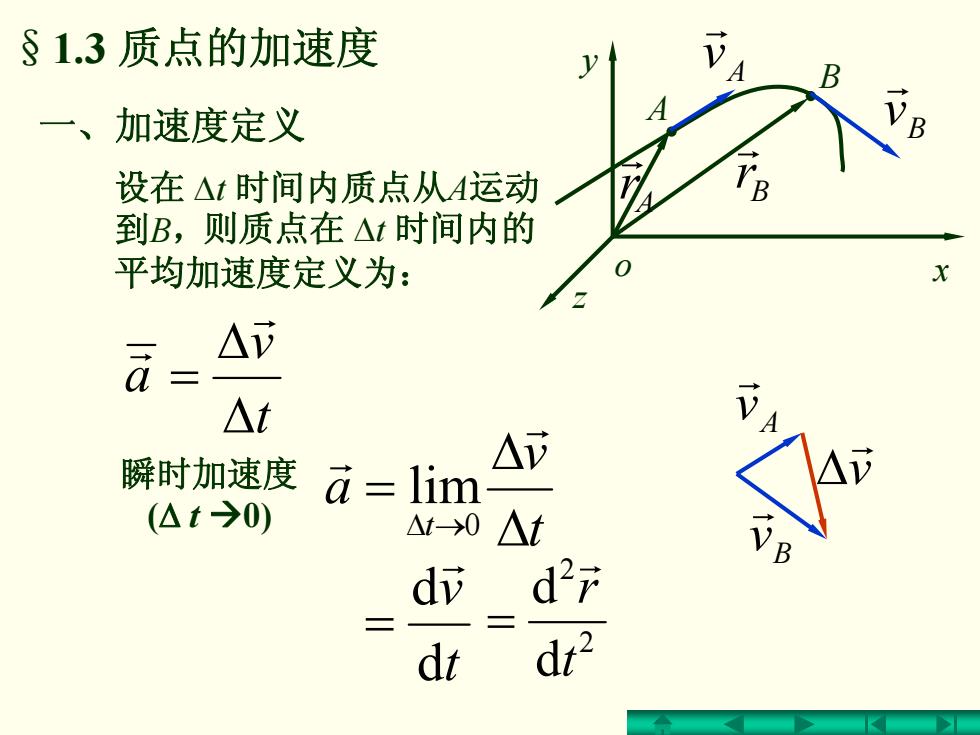
§1.3质点的加速度 1) A B 一、加速度定义 A 设在△t时间内质点从A运动 到B,则质点在△t时间内的 平均加速度定义为: a △ △t 瞬时加速度 a=lim △ (△t>0) △t->0 △t d d2分 dr dr
§1.3 质点的加速度 t v a Δ Δ = r r 瞬时加速度 ( Δ t Æ0) t v a t Δ Δ = →Δ r r 0 lim 一、加速度定义 t v d d r = 2 2 d d t r r = y x z o A B Ar r Br r B v r A v r B v r A v r v r Δ 设在 Δ t 时间内质点从A运动 到 B ,则质点在 Δ t 时间内的 平均加速度定义为:

二、加速度的分量形式 1.直角坐标系 d dv, a- dv-k dt dt dt dt d2 d&三k =a,i a,j+a.元 dx ◆ax= etc. dt
k t v j tv i tvx y z dd dd dd ++= 1. 直角坐标系 二、加速度的分量形式 k t z j ty i tx 2 2 2 2 2 2 d d d d d d ++= kajaia ++= zyx etc. , d d d d 2 2 t x t v a x x == t v a d dr r =

2.自然坐标系 e,(t) =v2= △e. dt e(t+△t) d a= d(ve) dt dt dv de e+ dt dr △e=e(t+△t)-e(t)
2. 自然坐标系 t t d d e t s evv rrr == t ev t v a d )(d d d t r r r == )()(tt t tetteer r r =Δ + Δ − o P1 P2 Δθ Δθ )(t ter )(t + Δtter t e r Δs Δ t e ve t v d d d d t t r r +=

大小:Ae=e△0=AB 2(t) △0:为e(t),e(t+△t)间的夹角P A.S 人0P △e △0→0:△e∥en e(t+△t) →△e=△0en de1im e1im △0 dθ en dt △t-→0 △t △t→0 △t en- dt dv ◆a= de, dv. d +v dt dt dt dt /0*
nt // : 0 eer r θ →Δ Δ ee tt Δ=Δ θ r r t n e e r r Δ⇒ = Δθ t e t e t Δ Δ = →Δ t 0 t lim d dr r t n d d d d e t ve t v θ rr += t e ve t v a d d d d t t r rr += n 0 lim e t t r ΔΔ = →Δ θ n dd e tθ r = = Δθ o P1 P2 Δθ Δθ )(t ter )(t + Δtter t e r Δs Δ 大小: )(),( : tt Δ + Δtteter r θ 为 间的夹角

dθ dθds dθ △0 e,(t) lim dt ds dt ds △s-0 △s △0 △e △s:P→P,间的路程 △5>0,△0>0 do △0 曲率:k= lim ds △1-→0 △S dv de. e+ dv do dt dt dt e+v dt
t n d d d d e t ve t v θ rr += t e ve t v a d d d d t t r rr += o P1 P2 Δθ Δθ )(t ter )(t + Δtter t e r t Δs Δ s st d d d d d dθ θ = s Δss Δ = →Δ θ θ 0 lim d d s θ →Δ→Δ 0,0 ss k t Δ Δ == →Δ θ θ 0 lim d d 曲率: 21 Δ : → PPs 间的路程
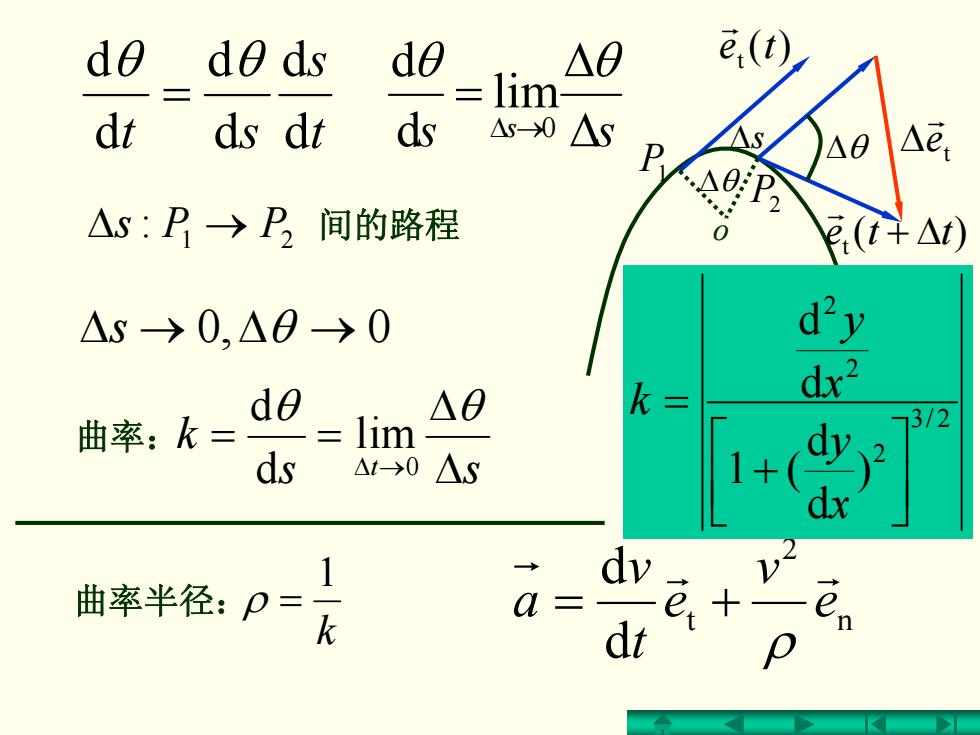
do d0 ds do △0 e,(t) lim dt ds di ds △s-0 △s A.S P △e △s:P→P,间的路程 .(t+△) △S>0,△0→0 d'y dθ △0 k= dx2 曲率:k= lim 3/2 ds △-→0△S dx 1 → dv 曲率半径:p= dt
n 2 t d d e v e t v a rr ρ += o P1 P2 Δθ Δθ )(t ter )(t + Δtter t e r t Δs Δ s st d d d d d dθ θ = s Δss Δ = →Δ θ θ 0 lim d d s θ →Δ→Δ 0,0 ss k t Δ Δ == →Δ θ θ 0 lim d d 曲率: 21 Δ : → PPs 间的路程 2/3 2 2 2 ) dd(1 d d ⎥⎦⎤ ⎢⎣⎡ + = x y x y k k 1 曲率半径:ρ =

dv 2 1) a e e,ar dt re. a=ae +a er dv d2s 切向加速度分量:4= dt 1 反映速度大小的变化: 法向加速度分量:a= 0 反映速度方向的变化!
n 2 2 t 2 ) d d ( 1 d d e t s e t s r r ρ += nntt eaeaa rr r = + p t e r a a n r a t n 2 t d d e v e t v a rrr ρ += 反映速度大小的变化! 反映速度方向的变化! 2 2 t d d d d t s t v 切向加速度分量: a == 2 n 1 va ρ 法向加速度分量: =

*圆周运动 dv a = dt D s d dθ V= (RO)=R dt dt dt dθ dt 0:角速度 dy do R do dt RB dt B dt 1 B:角加速度 a (Ro)-Ro 0
*圆周运动 * t s v d d = t v a d d t = 2 n 1 va ρ = n 2 t d d e v e t v a rrr ρ += β ω = d t d t R d d θ )( = d d R θ t = = R ω t R d d ω = = R β 2 )( 1 R ω R = 2 = R ω R θ s o ω θ = d t d ω : 角速度 β : 角加速度

运动学两类问题 1.已知:下=(t),求:(t),(t) d r 方法:求导数 ,a= dr dr 2.已知:(t)或(t),求:下(t) 方法:求积分 初值问题
* 运动学两类问题 运动学两类问题* ——初值问题 tatvtrr )(),( )( r r r r 1. 已知: ,求: = 2 2 d d , d d t r a t r v r r r r 方法:求导数 == trtvta )( ,)( )( r r r 2. 已知: 或 求: 方法:求积分