
國 第九章麦克斯韦方程与电磁波
第九章 麦克斯韦方程与电磁波

电磁学09.01:麦克斯韦方程组(参考赵凯华教程) 口电磁场规律: ∮Ds=jpdr V.D=Po 两个闭合面积分 aB VxE=- aB 两个闭合线积分 --1 8t → 两个梯度点乘 B.d5=0 7.B=0 两个梯度叉乘 fi=+识s V×H=j0+ aD 8t 8t 口存在介质时,须有介质方程: 洛伦兹力(微观): D=EE0E Jo=(E+E) 于=QE+Q(×B) j。=o(E+F×B) B=4,4H
电磁学09-01: 麦克斯韦方程组 (参考赵凯华教程) 电磁场规律: 0 0 0 0 0 ( 0 ) S V L S S L S D B E t B D dS d B E dl dS t B dS D H dl H j D j t dS t 存在介质时,须有介质方程: 0 * 0 0 0 0 ( ) ( ) r r D E j E j E j Ev B B E H 洛伦兹力 (微观 ): f QE Q v B ( ) 两个闭合面积分 两个闭合线积分 两个梯度点乘 两个梯度叉乘

电磁学0901:麦克斯韦方程组 口方程组的物理意义: >通过任意闭合面的电位移通量等于该曲面所包围的自 由电荷的代数和。 >电场强度沿任意闭曲线的线积分等于以该曲线为边界 的任意曲面的磁通量对时间变化量的负值。 >通过任意闭合面的磁通量恒等于零。 >稳恒磁场沿任意闭合曲线的线积分等于穿过以该曲线 为边界的曲面的全电流
电磁学09-01: 麦克斯韦方程组 方程组的物理意义: 通过任意闭合面的电位移通量等于该曲面所包围的自 由电荷的代数和。 电场强度沿任意闭曲线的线积分等于以该曲线为边界 的任意曲面的磁通量对时间变化量的负值。 通过任意闭合面的磁通量恒等于零。 稳恒磁场沿任意闭合曲线的线积分等于穿过以该曲线 为边界的曲面的全电流

圆电磁学09-01:麦克斯韦方程组 口方程组+介质性质方程:电磁场规律! >方程组加上边界条件的解是唯一的—这种客观条件下所发 生的真实的电磁场; >对电磁场,方程组中电荷、电流应看作是外来已知量,它们 的分布加上电磁场内介质的分布确定了电磁场的外部条件: >Maxwel方程组、洛伦兹力公式以及电荷守恒定律一 组成 电动力学的基本方程式,与力学定律结合。 口可解决: >运动带电体与电磁场所组成的力学体系的运动规律; >1 MaxwelⅡ方程组在洛伦兹变换下具有不变性(电动力学)
电磁学09-01: 麦克斯韦方程组 方程组+介质性质方程:电磁场规律! 方程组加上边界条件的解是唯一的——这种客观条件下所发 生的真实的电磁场; 对电磁场,方程组中电荷、电流应看作是外来已知量,它们 的分布加上电磁场内介质的分布确定了电磁场的外部条件; Maxwell方程组、洛伦兹力公式以及电荷守恒定律——组成 电动力学的基本方程式,与力学定律结合。 可解决: 运动带电体与电磁场所组成的力学体系的运动规律; Maxwell 方程组在洛伦兹变换下具有不变性(电动力学)

國电磁学09-01:麦克斯韦方程组 口边界条件问题: >界面上介质的性质有一突变,将导致静电场也会有突变; >积分形式的Maxwel方程在边界上依然成立,可以把不同介 质的场量用积分方程联系起来; >微分形式只适用于非边界区域,对于边界突变处,微分形式 已失去意义; >通常用积分方程不能直接求得空间各点场量的分布,要将方 程的积分形式变换成微分形式。 必须考虑用新的形式来给出边界上各物理量的关系,亦即给 出边界条件。 >边界条件就是把积分方程放到边界突变处得到的结果
电磁学09-01: 麦克斯韦方程组 边界条件问题: 界面上介质的性质有一突变,将导致静电场也会有突变; 积分形式的Maxwell 方程在边界上依然成立,可以把不同介 质的场量用积分方程联系起来; 微分形式只适用于非边界区域,对于边界突变处,微分形式 已失去意义; 通常用积分方程不能直接求得空间各点场量的分布,要将方 程的积分形式变换成微分形式。 必须考虑用新的形式来给出边界上各物理量的关系,亦即给 出边界条件。 边界条件就是把积分方程放到边界突变处得到的结果

厦电磁学0901:麦克斯韦方程组 ▣多类边界条件 电介质边界条件 Du D2>En=E2 i:(D2-D)=0,i×(E2-E)=0 磁介质边界条件 Ba=Be:Hn=H2 n(B2-B)=0,n×(H2-H)=0 导体界面电荷条件 -(i-)=-o 高频情况下真空界 i=Kn=ixH外 面条件 表面 导体内部
电磁学09-01: 麦克斯韦方程组 多类边界条件 电介质边界条件 磁介质边界条件 导体界面电荷条件 高频情况下真空界 面条件 1 21 2 2 1 21 , ( ) 0, ( ) 0 DDEE n ntt nD D n E E 1 21 2 21 2 1 , ( ) 0, ( ) 0 BBHH nn t t nB B n H H 0 02 01 nj j ( ) t m i k nH 外
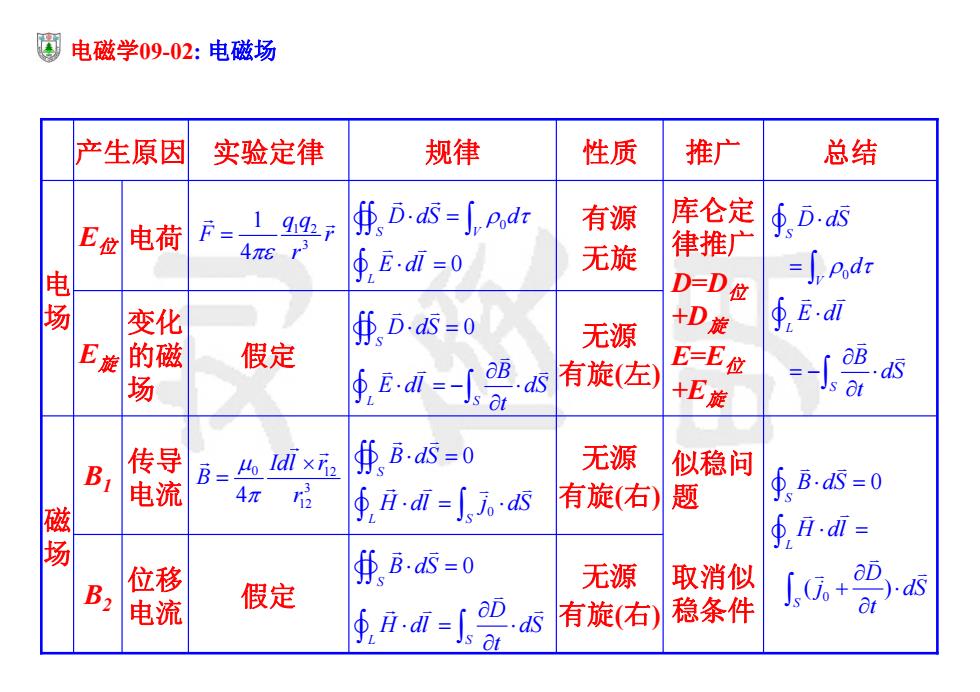
电磁学09.02:电磁场 产生原因 实验定律 规律 性质 推广 总结 有源 库仑定 E位电荷 F=19 ∯DS=∫pdr ∮D-as 4πer3 ∮Edi=0 无旋 律推广 D-D位 =5,Podr 场 变化 ∯Da否=0 无源 +D旋 ∮E-n E旋的磁 假定 E=E位 场 ∮i- B5有旋(左) +E旋 aB.dS 无源 Bi 传导 B=凸团× ∯B5=0 似稳问 电流 4π ∮H:i=〔j 有旋(右) 题 ∮B5=0 磁 ∮月dl= 位移 fB5=0 无源 取消似 B2 )d5 电流 假定 ∮idi= D d 有旋(右) 稳条件 +9 )s at
电磁学09-02: 电磁场 似稳问 题 取消似 稳条件 无源 有旋(右) 传导 电流 B1 库仑定 律推广 D=D位 +D旋 E=E位 +E旋 有源 无旋 E位 电荷 B2 E旋 无源 有旋(右) 假定 位移电流 磁 场 无源 有旋(左) 假定 变化 的磁 场 电 场 产生原因 实验定律 规律 性质 推广 总结 1 2 3 1 4 q q F r r 0 0 S V L D dS d E dl 0 S L S D dS B E dl dS t 0 12 3 12 4 Idl r B r 0 0 S L S B dS H dl j dS 0 S L S B dS D H dl dS t 0 S V L S D dS d E dl B dS t 0 0 () S L S B dS H dl D j dS t

圈电磁学09.03:电磁波的数学 ▣ 一些物理基础实验现象: ▣Dipole Antenna Microwave Interference 高 Microwave Polarization Telegraph Transmitter
电磁学09-03: 电磁波的数学 一些物理基础实验现象: Dipole Antenna Microwave Interference Microwave Polarization Telegraph Transmitter

电磁学09.03:电磁波的数学 口波动方程:无自由电荷、无传导电流、各向同性 V.D=Po V,E=0 D=E0EE VxE=- aB aH 8t P=0 了×E=-44 V.B=0 B=MouH V.i=0 aD 8t j6=0 V×H=6 OE 8t 口绝好的相似性、对称性、关联性!
电磁学09-03: 电磁波的数学 波动方程:无自由电荷、无传导电流、各向同性 0 0 0 0 0 0 0 0 0 0 0 0 0 D E B H j D E B H E E t t B H D E H j H t t 绝好的相似性、对称性、关联性!

厦电磁学09.03:电磁波的数学 A×(B×C) >激动人心的变换之一: 电场波动 =(4.C)B-(4.B)C V×(V×高=VV.-vEV-E=0=-v元 如果初始电场 VxE--m aH aH Vx(VxE)=V 或磁场取空间 波的形式,则 其一定会自发 .-7E=V× aH 在空间传播! 一一1 OE a(aE V×H=6E-VE=-(40c6 T.E=0 at at V×E=-4 oH .VE=(4μ)(88 a2E,1/-(44eE)12E at v.i=0 v2 8t2 OE V×H=6o8 aE I =v22E 4=1,8=1 in vacuum OE 0r2 8t2 =c2V2E
电磁学09-03: 电磁波的数学 激动人心的变换之一:电场波动 2 2 2 0 0 2 0 0 2 0 00 2 2 0 0 2 0 0 1/ ( ( )( ) ( ) ( ) , ( )( ) ( )( ) E v E EE E H H E E t t H E H t t E E H E t tt E E t 2 2 22 22 2 2 2 2 2 0 1, 1 in vacuum )( ) 1 E E vE cE t t E v t ( ) ( )( ) A BC A CB A BC 如果初始电场 或磁场取空间 波的形式,则 其一定会自发 在空间传播! 0 0 0 0 E H E t H E H t