
第1章质点运动学 §1.1基本概念 §1.2质点的位移和速度 §1.3质点的加速度 §1.4相对运动
第 1 章 质点运动学 §1.1 基本概念 §1.2 质点的位移和速度 §1.3 质点的加速度 §1.4 相对运动
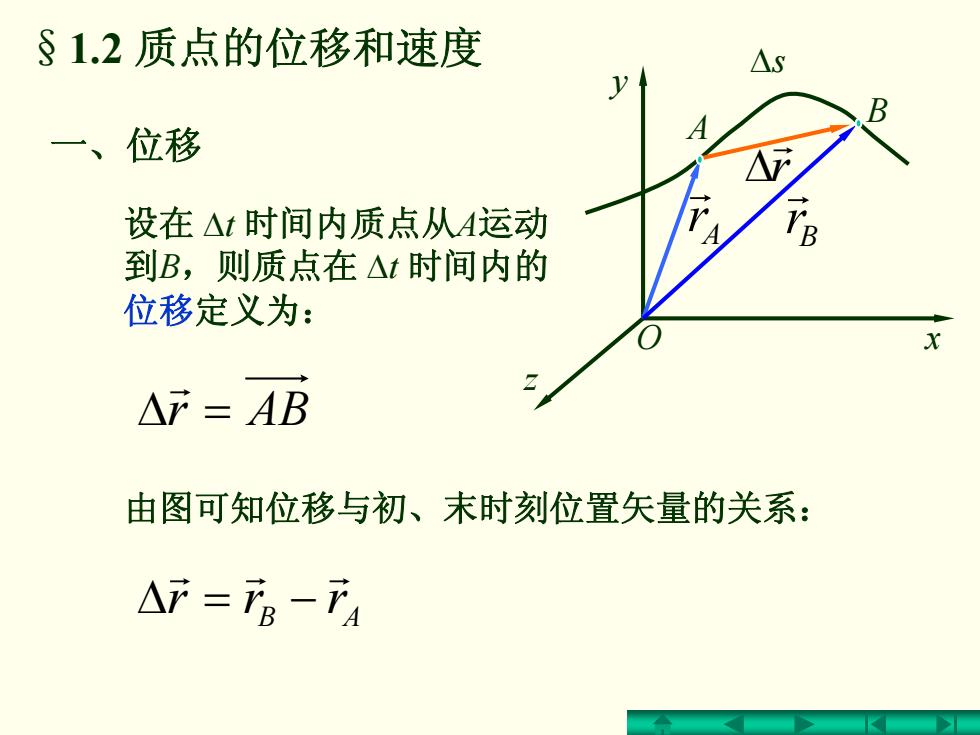
§1.2质点的位移和速度 一、位移 设在△t时间内质点从A运动 到B,则质点在△t时间内的 位移定义为: △产=AB 由图可知位移与初、末时刻位置矢量的关系: △产=2-7
一、位移 Δ = ABrr r §1.2 质点的位移和速度 r Δ Ar r Br r y x z O Δs A B 设在 Δt 时间内质点从A运动 到B,则质点在 Δt 时间内的 位移定义为: AB rrr r r r Δ = − 由图可知位移与初、末时刻位置矢量的关系:

位移的性质: 1.矢量性 如图所示:位移满足矢量叠加性质。 即在△t,+△t,时间内的 B 总位移满足: △t, AC=AB+BC △t,+△t2 直角坐标系中: F=xi+财+zk △产=△xi+△yi+△zk
A B C 1 Δt 21 Δ + Δtt 2 Δt += BCABAC kzjyixr kzjyixr rr r r r r r r Δ+Δ+Δ=Δ ++= 位移的性质: 1. 矢量性 如图所示:位移满足矢量叠加性质。 即在Δt1+ Δt2时间内的 总位移满足: 直角坐标系中:
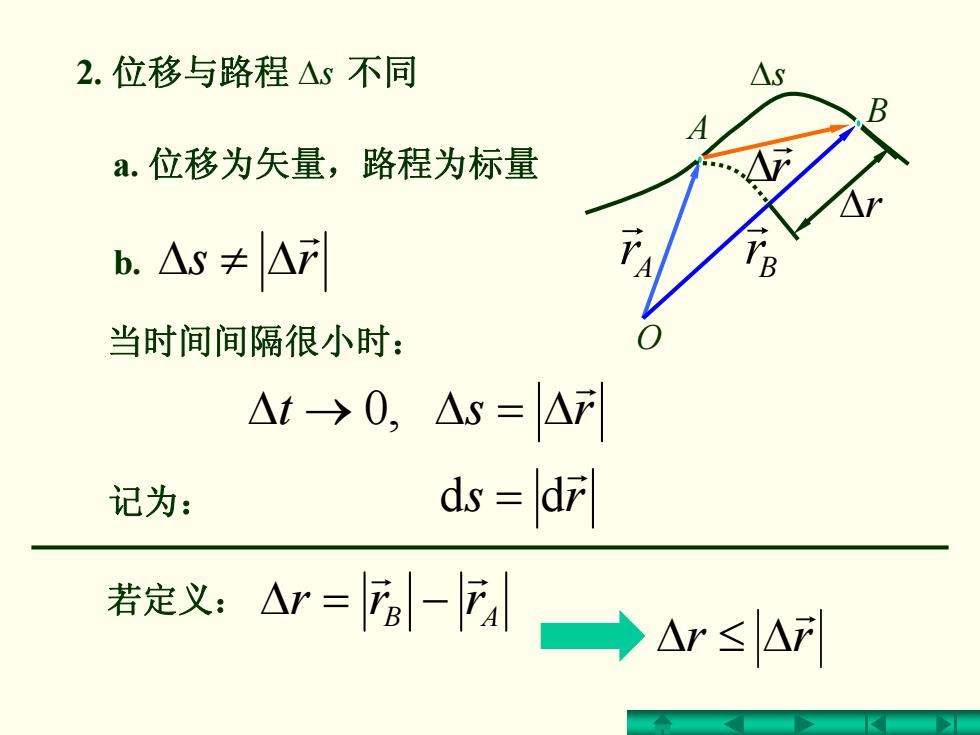
2.位移与路程△s不同 △S a.位移为矢量,路程为标量 b.△s≠△ 当时间间隔很小时: △t→0,△s=△F 记为: ds dF 若定义:Ar=-F→Ar≤A网
2. 位移与路程 Δs 不同 rst r ,0 Δ=Δ→Δ rs r = dd AB rrr r r −=Δ rr r Δ ≤ Δ r r Δ Ar r Br r O Δs A B 当时间间隔很小时: 记为: 若定义: Δr a. 位移为矢量,路程为标量 rs r b. Δ≠Δ
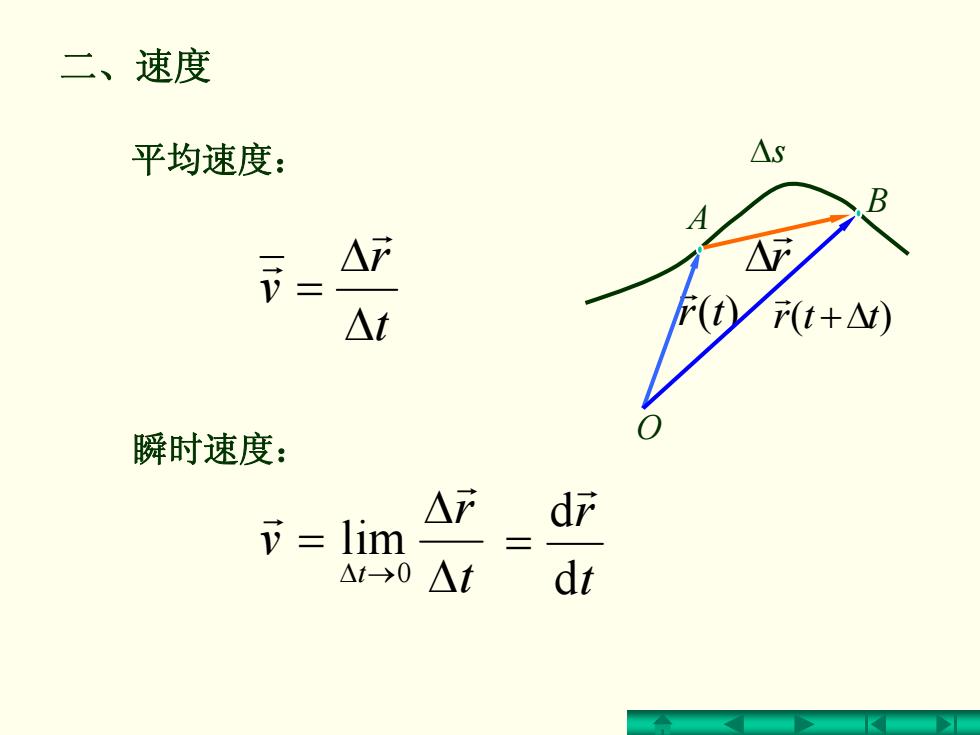
二、速度 平均速度: △S △ △t F(t+△) 瞬时速度: △ dr lim △t→0 △t dt
二、速度 t r v Δ Δ = r r 平均速度: 瞬时速度: t r v t Δ Δ = →Δ r r 0 lim t r d dr = r r Δ tr )(r +Δttr )(r O Δs A B

注意:速度为矢量! (1)方向 △t→0时, e B→A,△产沿A点处轨道的切线方向 (2)大小 d v= = lim r(t+△) dr △t-→0△t 1im△s=liml△ △t→0 △t→0 △S ∴.v=lim ds 速度大小与速率相等! △t-→0△t dt
t r vv d dr r == rs t t r Δ=Δ →Δ 0 →Δ 0 limlim t s v t Δ Δ =∴ →Δ 0 lim 注意:速度为矢量! (1) 方向 (2) 大小 速度大小与速率相等! t e r t r t Δ Δ = →Δ r 0 lim t s d d = r r Δ tr )(r +Δttr )(r O Δs A B rAB r → , Δ 沿A点处轨道的切线方向 t →Δ 0 时

三、速度的分量形式 1.直角坐标系 dr di+dyj+ k dt dt dt dt 正=yxi+yj+vk dx →x= etc. dt 速率: v=吲=V?++
t r v d dr r = vv r 速率: = 三、速度的分量形式 1. 直角坐标系 kvjvivv ++= zyx r k t z j ty i tx dd dd dd ++= 222 zyx ++= vvv etc. , d d t x vx =
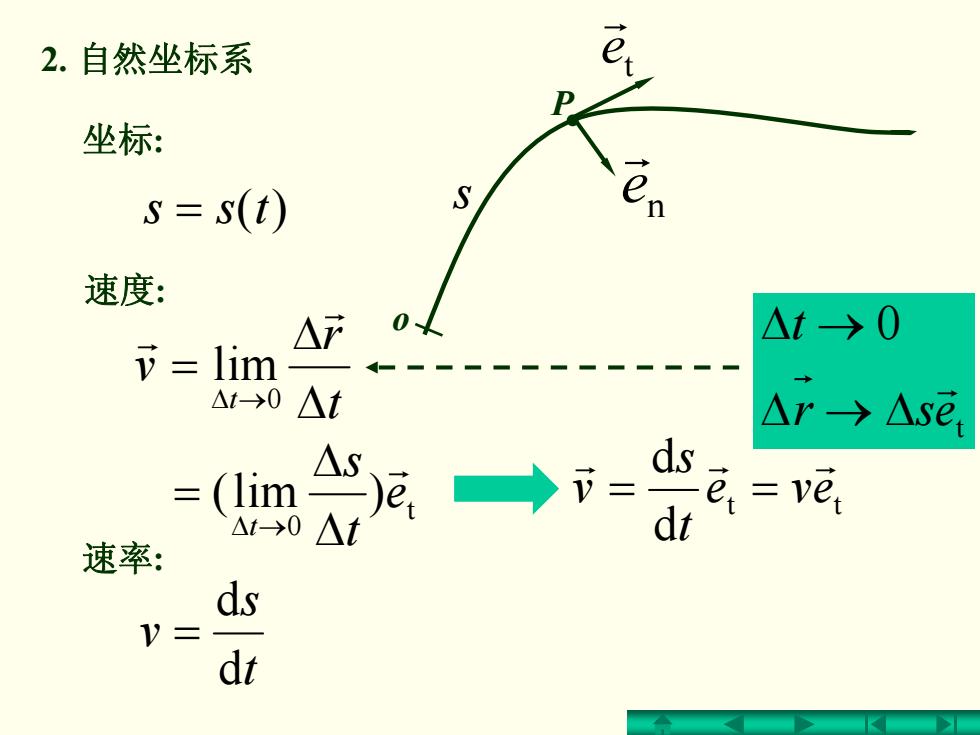
2.自然坐标系 坐标: s=s(t) 速度: △7 △t→0 lim △t-→0 △t △r→△se, △ (lim e,→= = △t→0 △t dt 速率: ds V= dt
t r v t Δ Δ = →Δ r r 0 lim 2. 自然坐标系 t s v d d = tt d d eve t s v rrr == = tss )( 速度: 速率: 坐标: o t e r s n e r t 0 )lim( e t s t r Δ Δ = →Δ t 0 esr t r Δ→Δ Δ → P
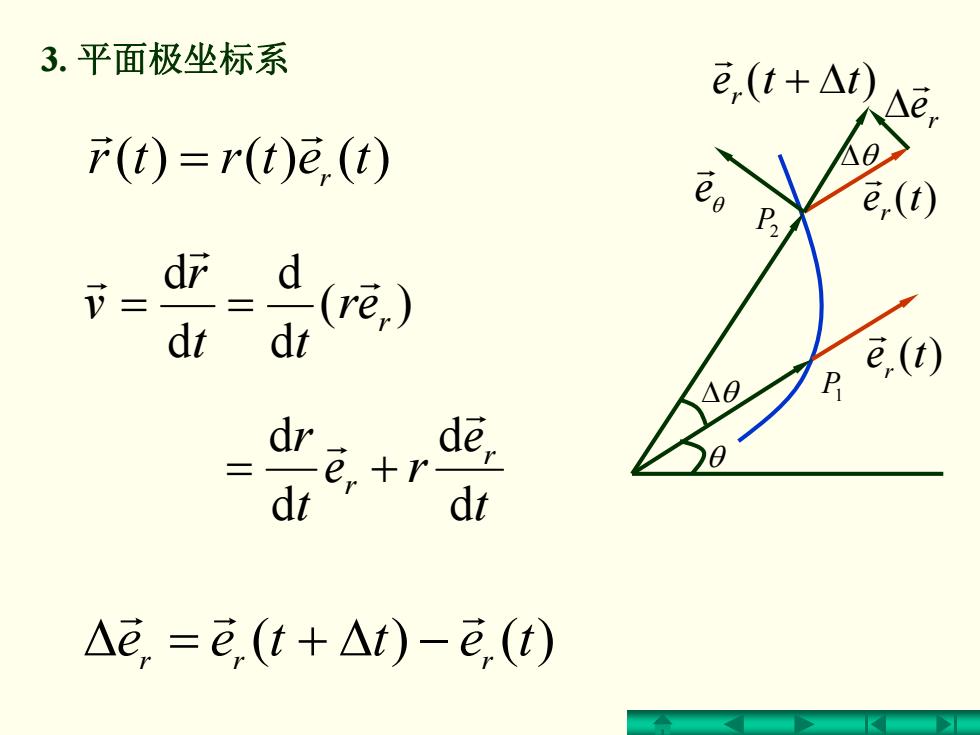
3.平面极坐标系 e(t+△t) e F(t)=r(t)e,(t) e,(t) d (re,) dt dt e0) dr de, e ,+r dt dt △e,=en(t+△t)-e(t)
tetrtr )()()( r r r = )( d d d d r er tt r v r r r == tettee )()(rr r r r r Δ = + Δ − θ e r tte )( r + Δ r te )( r r te )( r r r e r Δ Δ θ Δ θ θ P1 P2 3. 平面极坐标系 t e re t r r r d d d d r r +=
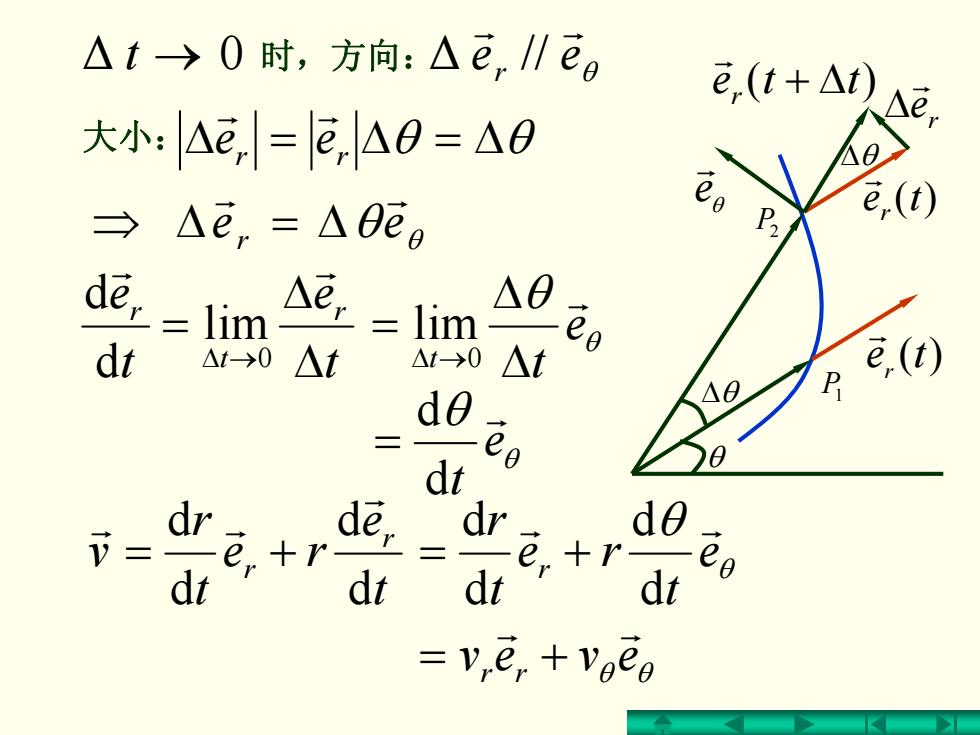
△t>0时,方向:△e,∥ee e,(t+△t) he, 大小:Ae,=e,A8=A0 →△e,=△0ea e,(t) de, lim △ r=lim △0 dt △t-→0 △t △t-→0 △t e,(t) d △0 dt dr D e,+r de r do e,+r- e dt dt dt dt v e,veeo
θ θ eer r r Δ⇒ = Δ θ θ e t t r Δ Δ = →Δ 0 lim t e t e r t r Δ Δ = →Δ r r 0 lim d d θ θ e t r d d = t e re t r v r r dd dd r rr += θ θ e t re tr r rr dd dd += θ e r tte )(r + Δ r te )(r r te )(r r r e r Δ Δθ Δθ θ P1 P2 θθevev rr r r = + θ t eer r r Δ → 时,方向: 0 Δ // ee rr Δ=Δ=Δ θθ r r 大小: