
第1章质点运动学 §1.1基本概念 §1.2质点的位移和速度 §13质点的加速度 §1.4相对运动
第 1 章 质点运动学 §1.1 基本概念 §1.2 质点的位移和速度 §1.3 质点的加速度 §1.4 相对运动

§1.4相对运动 一、运动描述的相对性 S系相对S系平动,速度为 S i 两个相对平动参考系 P(x,y,z) (x',y,z') y X 元='+R 对质点位置(矢量)描述的相对性!
§1.4 相对运动 = ′ + Rrrr r 两个相对平动参考系 对质点位置(矢量)描述的相对性! 一、运动描述的相对性 y y ' o P o ' x x ' S S' (x, y, z ) (x', y', z' ) y' u r r r r′ r R r S'系相对S系平动,速度为ur

利用速度和加速度定义: F=T+R dr dR dr' d dR dt dt dt t:S参考系时间下= u= dr dr d27d2R,d27 dr' d 如果t=t则: dt2 dr dr' du →下=+ a =a'+ dt 牵连速度 牵连加速度 dt
= ′ + Rrrr r 利用速度和加速度定义: t r t R t r d d d d d d ′ += r r r 2 2 2 2 2 2 d d d d d d t r t R t r ′ += r r r t u aa d dr rr = ′ + uvv = ′ + r r u r t u d dr 牵连速度 牵连加速度 t R u t r t v d d d d : r r r r S 参考系时间 == v t r t r tt = ′ ′ ′ = ′ ′ = r r r d d d d 如果 则:
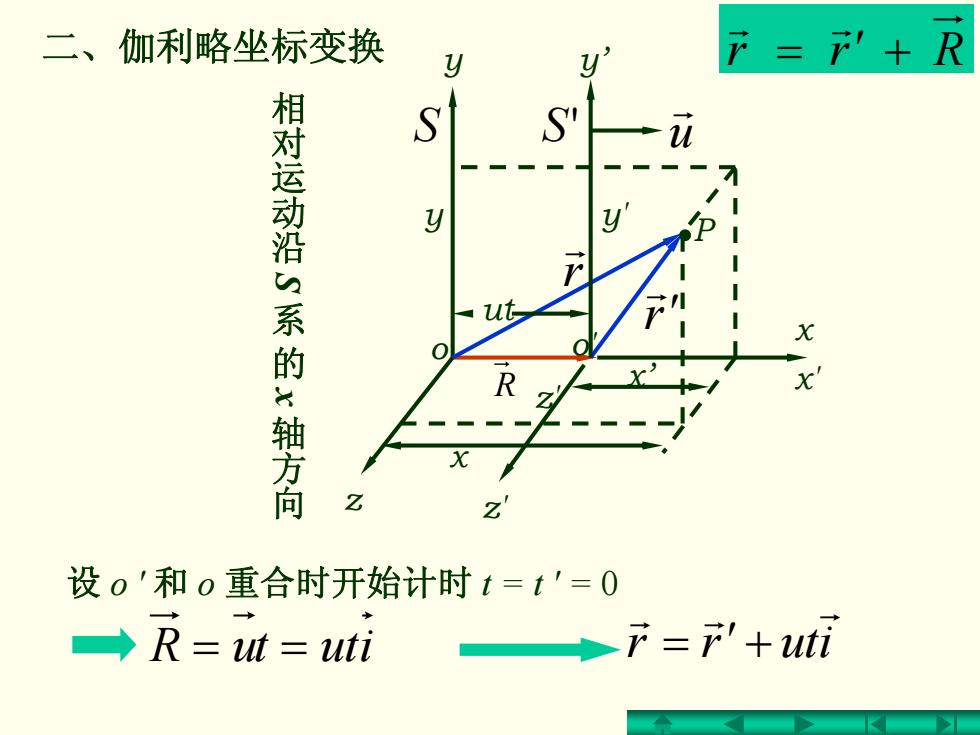
二、伽利略坐标变换 y y F=十R u 相对运动沿系的x轴方向 y 设0'和o重合时开始计时t=t'=0 →R=t=uti ◆下='+uti
二、伽利略坐标变换 相对运动沿 S 系的 x 轴方向 iutrrr r r = ′ + 设 o ' 和 o 重合时开始计时 t = t ' = 0 == iuttuR = ′ + Rrrr r y y’ x' x x’ x z z' y' o o' y ut z' u r r r r ′ r P R S S

写成分量形式: X x"+ut y 伽利略(Galilean)时 空坐标变换。 Z z 设o'和o重合时开始计时t=t'=0 →R=t=uti r=r'+uti END
写成分量形式: ⎪⎪⎩ ⎪⎪⎨⎧ = ⎪⎩ ⎪⎨⎧ = = += ' ' ' ' tt zz yy utxx 伽利略(Galilean) 时 空坐标变换。 END = ′ + iutrrr r 设 o ' 和 o 重合时开始计时 t = t ' = 0 == iuttuR