
第11章静电场 §11.1静电学基本问题 §11.2电场电场强度 §11.3高斯定理及应用 §11.4环路定理与电势 §11.5电势与电场强度的关系 静电场部分习题果内容
第 11 章 静电场 §11.1 静电学基本问题 静电学基本问题 §11.2 电场 电场强度 §11.3 高斯定理及应用 高斯定理及应用 §11.4 环路定理与电势 环路定理与电势 §11.5 电势与电场强度的关系 电势与电场强度的关系 静电场部分习题课内容 静电场部分习题课内容

§11.3高斯定理及应用 一、 电场线 通常用一簇空间曲线形象描述场强的空间分布一 称为电场线。 (1)方向:场线上每一点的切线方向与该处的电 场强度方向相同; (2)密度:在该点取一垂直于场强方向的面积元, 使通过单位面积的电场线数目满足: dN -E dS
(2)密度:在该点取一垂直于场强方向的面积元, 使通过单位面积的电场线数目满足: §11.3 高斯定理及应用 高斯定理及应用 一、电场线 通常用一簇空间曲线形象描述场强的空间分布—— 称为电场线。 (1)方向:场线上每一点的切线方向与该处的电 场强度方向相同; E S N = ⊥ d d E v dS⊥

*电场线的特征米 >电场线起自于正电荷或无穷远,止于负 电荷或无穷远,没有电荷处不中断; >两条电场线不会相交,不能相切! >电场线不可能是闭合曲线
¾两条电场线不会相交,不能相切! *电场线的特征* ¾电场线起自于正电荷或无穷远,止于负 电荷或无穷远 ,没有电荷处不中断; ¾电场线不可能是闭合曲线
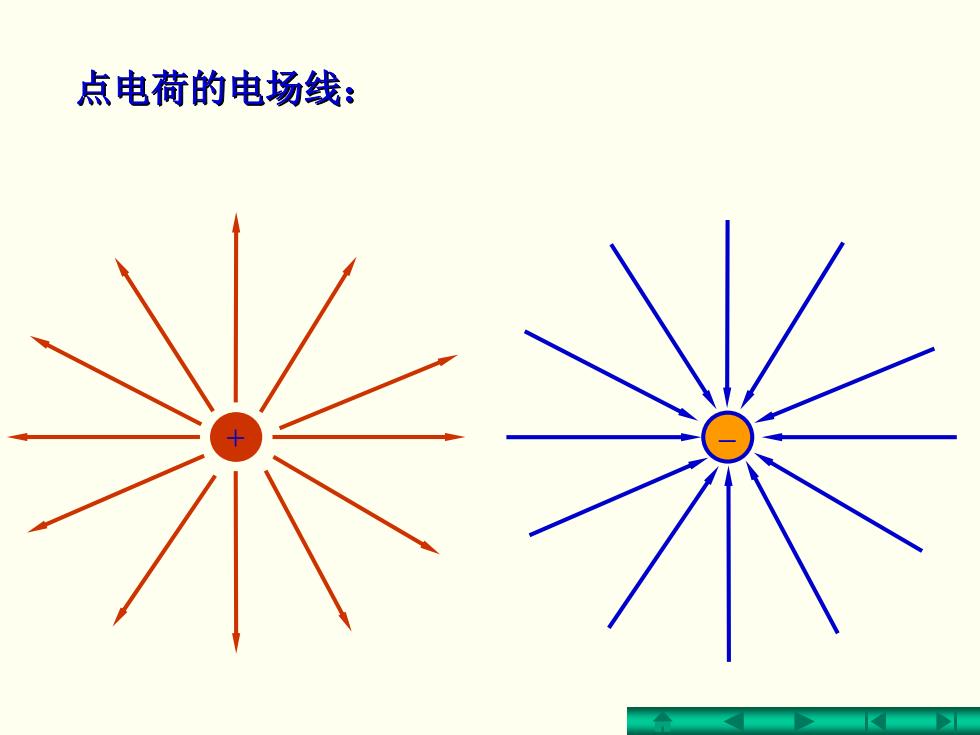
点电荷的电场线:
点电荷的电场线: 点电荷的电场线: + –

儿种典型带电系统的电场线
几 种 典 型 带 电 系 统 的 电 场 线
二、电通量 匀强电场 定义面元和通过面元的 电通量: ds dse, en— 面元的法向单位矢量 ds, ds →dΦ=E.d5 按定义: dΦ=EdS cos 0 EdS dN 通过面元dS的电通量与通过面元dS的电场 线的条数相等!
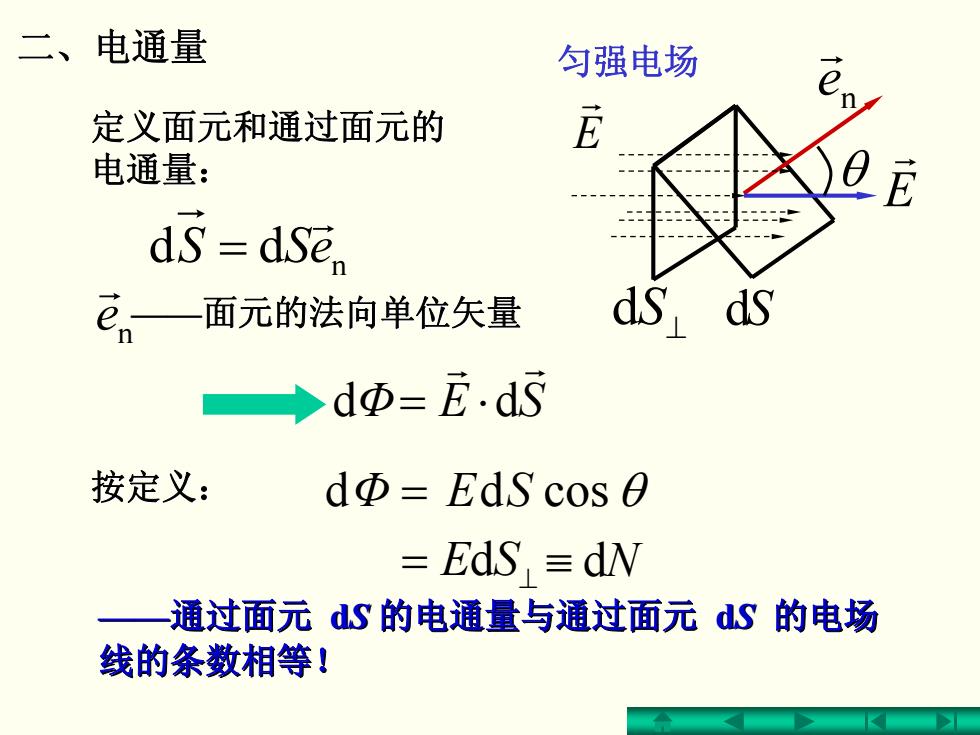
dS n e r r E = dSE ⊥ E r dd n eSS r = Φ = SE cosdd θ Φ SE r r ⋅= dd 二、电通量 匀强电场 θ 定义面元和通过面元的 定义面元和通过面元的 电通量: n e r ——面元的法向单位矢量 面元的法向单位矢量 dS⊥ ≡ dN ——通过面元 dS 的电通量与通过面元 的电通量与通过面元 dS 的电场 线的条数相等! 线的条数相等! 按定义:

通过任意曲面的电通量如何计算? 按数学的办法:把曲面切割成无穷多个面元,每 面元处可视为匀强电场 dΦ=E.dS 对曲面S总的电通量 -[E.ds
∫ Φ= dΦ 按数学的办法:把曲面切割成无穷多个面元,每 一面元处可视为匀强电场 ∫ ⋅= S SE 通过任意曲面的电通量如何计算? r r d 对曲面 S 总的电通量 S Φ SE dS r r ⋅= dd Ev
讨论 E ds 。dΦ=龙.d5的正、负取决于面元 的法线方向与电场强 度方向的关系。 如图所示: E.d5>0 若面元法向相反: E.d5<0 ·通过闭合曲面的电通量 规定闭合曲 面法线方向 -fE-as 向外为正!
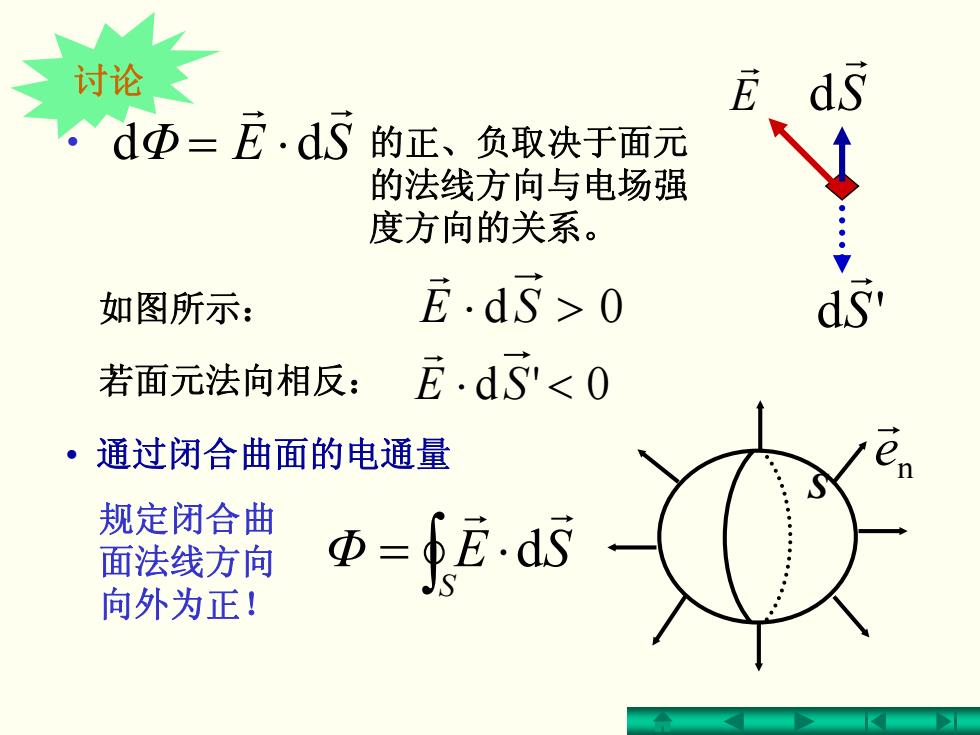
• 通过闭合曲面的电通量 ∫ ⋅= S Φ SEr r d Φ SE r r • ⋅= dd 的正、负取决于面元 的法线方向与电场强 度方向的关系。 S r d rE 如图所示: SE >⋅ 0d r 若面元法向相反: SE <⋅ 0'd r S 规定闭合曲 面法线方向 向外为正! n e r S'd r 讨论
E.ds电场线穿入,每一根电场 线对电通量的贡献为-1。 E.d5>0 dS" >电场线穿出,每一根电场 线对电通量的贡献为1。 通过闭合曲面的电通量 规定闭合曲 面法线方向 向外为正! -fE-d5
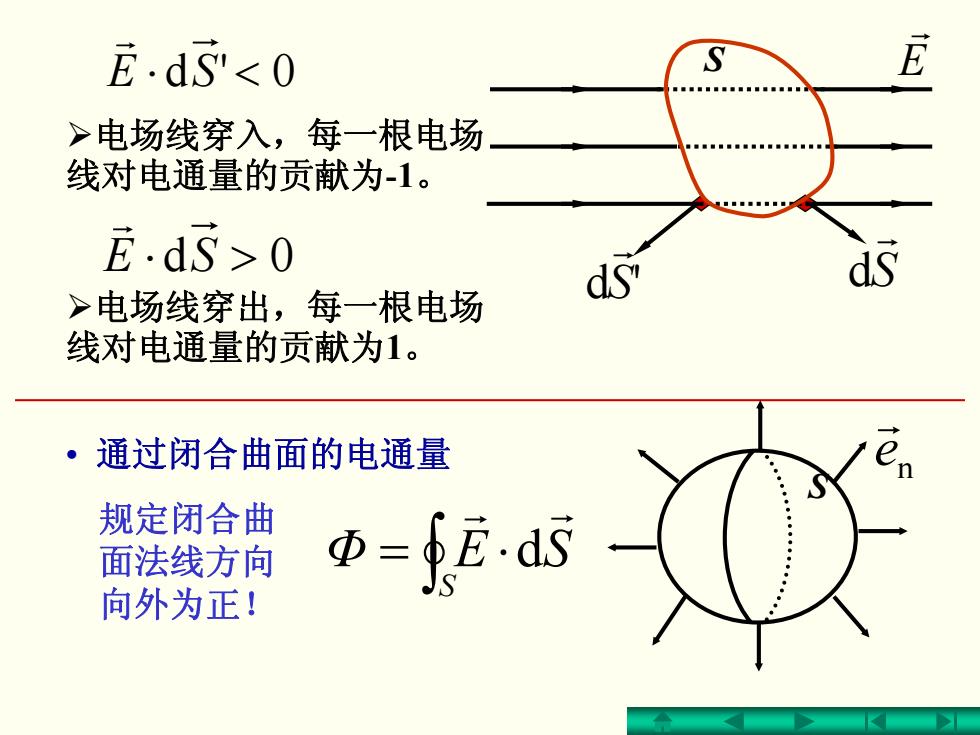
S'd r S r d SE >⋅ 0d r SE <⋅ 0'd r ¾电场线穿入,每一根电场 线对电通量的贡献为-1。 ¾电场线穿出,每一根电场 线对电通量的贡献为1。 • 通过闭合曲面的电通量 ∫ ⋅= S Φ SEr r d S 规定闭合曲 面法线方向 向外为正! n e r E r S

三、静电场的高斯定理 在真空中的电场内,通过任一闭合曲面的电通量等 于这闭合面所包围的电量代数和的1/e倍。 Es=Σ9 (不连续分布源电荷) f瓦.dS=。J川d业(连续分布游电荷) 一S称为Gauss面
三、静电场的高斯定理 三、静电场的高斯定理 在真空中的电场内, 通过任一闭合曲面的电通量等 于这闭合面所包围的电量代数和的1/ ε 0倍。 ∫ =⋅ ∑i i S qSE 0 1 d ε r (不连续分布源电荷) ∫∫∫∫ =⋅ S V SE d V 1 d 0 ρ ε r (连续分布源电荷) —— S 称为 Gauss 面