
第9章热力学定律 §9.1内能功和热量 准静态过程 §9.2热力学第一定律热容 §9.3绝热过程多方过程 §9.4循环过程卡诺循环过程 §9.5热力学第二定律 §9.6热力学过程的不可逆性 §9.7热力学系统的熵 §9.8熵增加原理 §9.9热力学第二定律的统计意义 熵的统计表述有序和无序
§9.1 内能 功和热量 准静态过程 第 9 章 热力学定律 §9.2 热力学第一定律 热容 §9.3 绝热过程 多方过程 §9.5 热力学第二定律 §9.6 热力学过程的不可逆性 §9.7 热力学系统的熵 §9.8 熵增加原理 §9.9 热力学第二定律的统计意义 熵的统计表述 有序和无序 §9.4 循环过程 卡诺循环过程
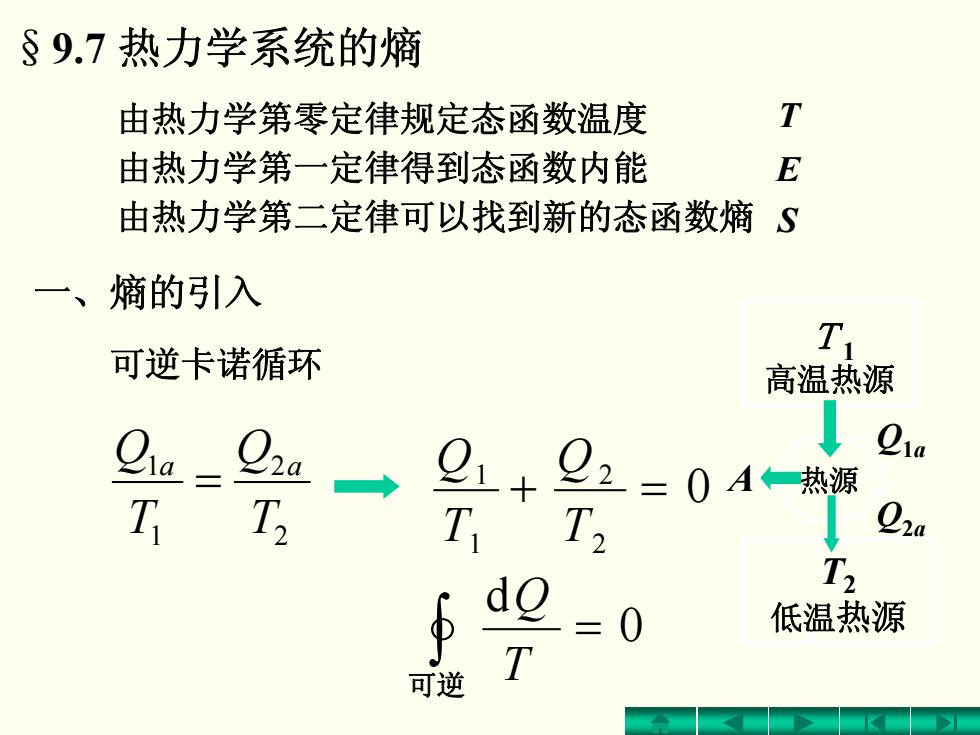
§9.7热力学系统的熵 由热力学第零定律规定态函数温度 T 由热力学第一定律得到态函数内能 E 由热力学第二定律可以找到新的态函数熵S 一、熵的引入 可逆卡诺循环 T 高温热源 22a ↓ 1 21a T T 2=0A一 T T, 22a do T 低温热源 T 可逆
由热力学第零定律规定态函数温度 T 一、熵的引入 可逆卡诺循环 0 2 2 1 1 =+ T Q T Q 2 2 1 1 T Q T Q aa = ∫ = 可逆 0 d T Q §9.7 热力学系统的熵 T 1 高温热源 T2 低温热源 A 热源 Q 1 a Q 2 a 由热力学第一定律得到态函数内能 E 由热力学第二定律可以找到新的态函数熵 S

任一可逆循环(图示) 绝热线 可以看作由许多微小卡 诺循环拼成,相邻两个 等温线 微小卡诺循环因过程相 反而大部分抵消,留下 一个锯齿形曲线一用 来近似替代可逆循环。 0 V 任一微小卡诺循环 02=0 Ta
可以看作由许多微小卡 诺循环拼成,相邻两个 微小卡诺循环因过程相 反而大部分抵消,留下 一个锯齿形曲线—— 用 来近似替代可逆循环。 任一可逆循环(图示) o V p 等温线 绝热线 任一 微小卡诺循环 Qi1 Qi2 Ti1 Ti2 0 2 2 1 1 =+ i i i i T Q T Q

所有微小卡诺循环叠加 无限细分锯齿曲线无限接近原来的可逆循环 do 入 克劳修斯等式 可逆 设可逆循环12b1 p 9鸭+兴=0 1 L 0 V
所有微小卡诺循环叠加 ∑ = 0 i i i T Q 无限细分锯齿曲线无限接近原来的可逆循环 ∫ = 可逆 0 d T Q 克劳修斯等式 设可逆循环 1 a 2 b 1 0 dd 21 12 =+= a ∫∫ b T Q T Q ∫ T d Q p o V 1 2 a b

J1b2 T 表明沿可逆过程的 d9的积分,只取决于始末状 态,而与过程无关。因此可以认为存在一个新的态函 数,克劳修斯称这个态函数为“熵”。 定义状态函数S: 52-8,=[2 T 可逆 9=2+9=0 0
定义状态函数 S: ∫ =− 21 12 dTQ SS 可逆 表明沿可逆过程的 的积分,只取决于始末状 态,而与过程无关。因此可以认为存在一个新的态函 数,克劳修斯称这个态函数为“熵”。 T dQ ∫∫ = 21 21 dd a b TQ TQ p o V 1 2 a b 0 dd 21 12 =+= a ∫∫ b TQ TQ ∫ TdQ

S,-s,=∫d 可逆 例如理想气体准静态绝热过程 ◆△S=0 对于微小过程 ds= do T 由热力学第一定律 do=dE+pdv →TdS=dE+pdV 综合了热力学第一、第二定律的可逆过程的基本 热力学关系式
对于微小过程 T Q S d d = = + ddd VpEQ = + ddd VpEST 例如理想气体准静态绝热过程 ΔS = 0 综合了热力学第一、第二定律的可逆过程的基本 热力学关系式。 ∫ =− 21 12 dTQ SS 可逆 由热力学第一定律

二、熵的计算 1.熵是态函数 2.熵是广延量 3.对可逆过程 52-S,=2d T 可逆 4.对不可逆过程 可以设计一个连接两状态可逆过程,计算相应 的熵变
3. 对可逆过程 4. 对不可逆过程 可以设计一个连接两状态可逆过程,计算相应 的熵变。 二、熵的计算 1. 熵是态函数 2. 熵是广延量 ∫ =− 21 12 dTQ SS 可逆

[例9-91试求1mol理想气体由初态(po,T。,',)经某一过 程到达终态(p1,T1,V)的熵变。 解: 4=∫9-∫+na T + = Cr.In Cr. Po Po
[ 例 9-9] 试求1mol理想气体由初态( p0 , T0 , V0 )经某一过 程到达终态( p 1 , T1 , V1)的熵变。 解: ∫∫ + == T VpE T Q S ddd Δ ∫∫ = + 1 0 1 0 m, d V d V T T V V V R T TC 0 1 0 1 m, lnln V V R T T = C V + 0 1 m, 0 1 m, ln ln V V C p p = C V + P 0 1 0 1 m, lnln p p R T T = CP −

To=T AS=RIn =-Rln P Po P。=乃 △S=Cr,m 。ln 二CP,m T Vo=VI 4S=PL-Cr.mn Po AS =Cr.m In T+RIn T △S>0 m In V P+Cp.m In Po =Cp.m In T RIn T Po
= TT 10 0 1 0 1 ln ln p p R V V Δ RS −== = PP 10 0 1 m, 0 1 m, ln ln T T C V V CS =Δ P = P =VV 10 0 1 m, 0 1 m, ln ln T T C p p Δ = CS V = V T S p V 0 Δ S > 0 1 0 1 m, lnln V V R T T CS =Δ V + 0 1 m, 0 1 m, ln ln V V C p p = C V + P 0 1 0 1 m, lnln p p R T T = CP −

三、温熵图 以心为横坐标,T为纵坐标 T 温熵图上一条曲线表示一个 准静态过程。 b 2 曲线下面积 S ['ras -g 温熵图又称示热图。 对于闭合曲线 0=A
= ∫ ba dST Q Q 三、温熵图 Q=A T S a b T S 以S 为横坐标,T 为纵坐标 温熵图上一条曲线表示一个 准静态过程。 曲线下面积 对于闭合曲线 温熵图又称示热图