
第16章变化的电兹场 §16.1电磁感应定律 §16.2动生电动势 §16.3感生电动势 感应电场 §16.4自感和互感 §16.5电容和电感电路中的暂态电流 §16.6磁场能量 §16.7位移电流 §16.8麦克斯韦电磁场方程组
第 16 章 变化的电磁场 §16.2 动生电动势 §16.1 电磁感应定律 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组 §16.5 电容和电感电路中的暂态电流

§16.2动生电动势 一、洛伦滋力产生动生电动势 设稳恒磁场乃,导线运动! 载流子受力户=q巾×B如q>0× B L s=瓦di=(xB)-df如s>0,sld 对于导线回路8=×d
§16.2 动生电动势 一、洛伦兹力产生动生电动势 设稳恒磁场 , r B × × × × × × × × × r B r l vr d a b BvqF r r r ×= Bv q F E r r r r k ×== ∫∫ ⋅×=⋅= ba ba lBvlE r r r r r d)(d k ε 对于导线回路 ( ) lBvl r r r ∫ ε ⋅×= d 如 q>0 l r 如 > εε d//,0 导线运动! 载流子受力

试证明:在稳恒磁场中,动生电动势 8=56×)= dΦm dt 证明: 如图△t时间内dl扫过面积 dS=dix△t 左、右底面和侧面构成闭合曲面S! 1(t+△)?? →乐Bd5=0 2> 作as-e体小-
(tl ) ( ) Δ+ ttl ′ l r d ′ dl r v r 证明:如图 Δt 时间内 l r d 扫过面积 dd ΔtvlS r r r ×= =⋅ 0d ∫∫S SBr r (dd Δ ) =⋅+×⋅+⋅− 0d l S′ ∫∫∫∫∫∫ l′ SBtvlBSB r r r r r r r ?? 试证明:在稳恒磁场中,动生电动势 ( ) t lBvl dd d Φm −=⋅×= ∫ r r r ε 左、右底面和侧面构成闭合曲面 S!

d(p×)=B.(×)=氵.(@×B) →f6×da1=B.d-川B.s) =一△Φ →0时,一8=6×= dΦ dr t)1(t+△t)?? dl @+瓜taxa0
( ) ( ) ∫ ∫∫∫∫ ⋅−⋅−=⋅×⇒ l l′ l SBSBtlBv r r r r r r r d Δ dd = −ΔΦ m Δt → 0时, βαγαγβγβα )()()( r r r r r r r r r Q ×⋅=×⋅=×⋅ ( ) t lBvl dd d Φ m ε −=⋅×= ∫ r r r (tl ) ( ) Δ+ ttl ′ l r d ′ dl r v r (dd Δ ) =⋅+×⋅+⋅− 0d l S′ ∫∫∫∫∫∫ l′ SBtvlBSB r r r r r r r ??

非闭合回路: e=["(vxB)-d7 1Φ dt dt时间内扫过 面积的磁通量
非闭合回路: t lBv b a d d d)( Φ m ε −= ⋅×= ∫ r r r dt 时间内扫过 面积的磁通量

电磁阻尼 金属片插入磁场,动生电动势在金属片内形成电流, 电流在磁场中受到安培力的作用,阻碍金属片的运动。 × × X××× ××
电磁阻尼 × × × × × × × × × × × × × × × × v r F r × × × × × × × × × × × × × × × × v r F r 金属片插入磁场, 动生电动势在金属片内形成电流, 电流在磁场中受到安培力的作用,阻碍金属片的运动

二、动生电动势过程中的能量转化 设均匀磁场B 以恒定外力向右拉杆 节个→I个→B1个 F=q(行+)×B =qg下×B+qd×B=f+方 不i=q×Bi=g⑧x正=-gax市=-方市 >外力做正功输入机械能,安培力做负功吸收它,同 时感应电动势在回路中做正功又以电能形式输出这个 份额的能量
二、动生电动势过程中的能量转化 设均匀磁场 r B 以恒定外力向右拉杆 r v r u 1f r ( ) BuvqF r r r r ×+= ( ) ( ) vfvBuqvuBquBvquf r r r r r r r r r r r r r ⋅−=⋅×−=⋅×=⋅×=⋅ 1 2 )( IBlIv ↑↑→↑→ ¾外力做正功输入机械能,安培力做负功吸收它,同 时感应电动势在回路中做正功又以电能形式输出这个 份额的能量。 r × × × × × × × × × × × × 2 f r 21 ffBuqBvq r r r r r r +=×+×=
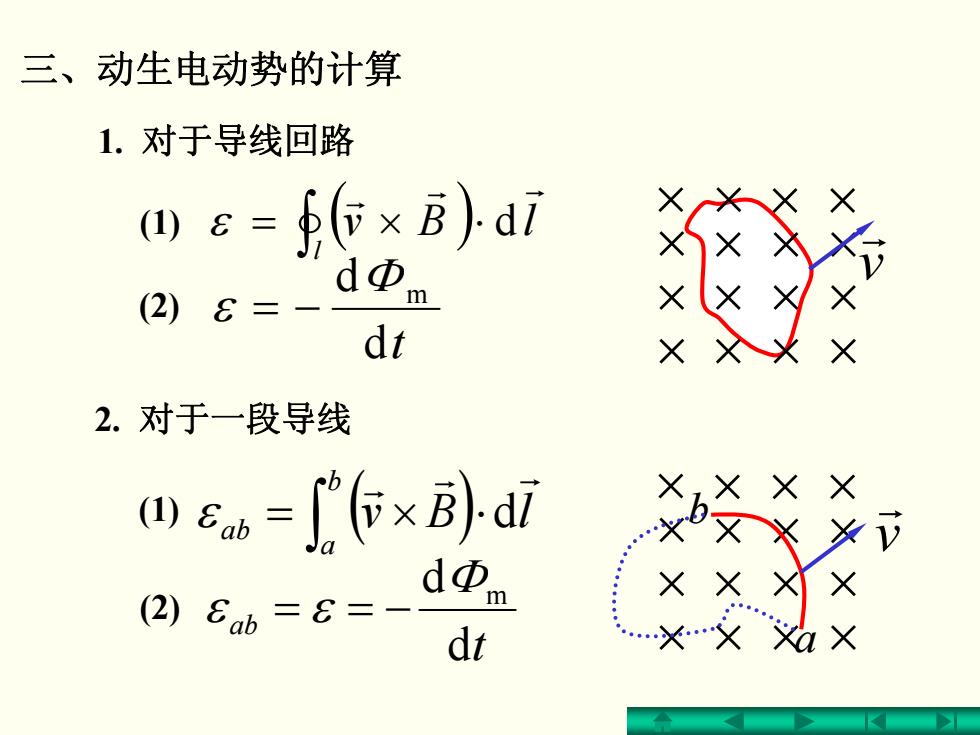
三、动生电动势的计算 1.对于导线回路 m) 效 (2)8= dt × 2.对于一段导线 田66=心6×)di X× (2)8b=8=- dt
三、动生电动势的计算 2. 对于一段导线 1. 对于导线回路 × × × × × × × × × × × × × × × × v r × × × × × × × × × × × × × × × × v r a b ( ) ∫ ⋅×= l lBv r r r (1) ε d t ab d d Φ m (2) εε −== ( ) ∫ ⋅×= b a ab lBv r r r (1) ε d d t d Φ m (2) ε −=

[例16-1川如图杆OA=L以角速度0绕0点转动, 且与直电流共面,求£。 解: B= oI 2πa+lcos0) de=(xB)-dI vBdl 41 =102πa+lcos0 d
[ 例16-1] = LOA求 ε 如图杆 以角速度 绕 ω O点转动 , 且与直电流共面, 。 I a o A θ l ω r d ( ) 解: θ μ 2 π cos 0 la I B + = ( ) lBv r r r d ε ⋅×= d = dlvB ( ) l la I l d 2 π cos 0 θ μ ω + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + == − ∫ a Laa L I θ θθ ωμ εε cos ln 2 πcos cos d 0
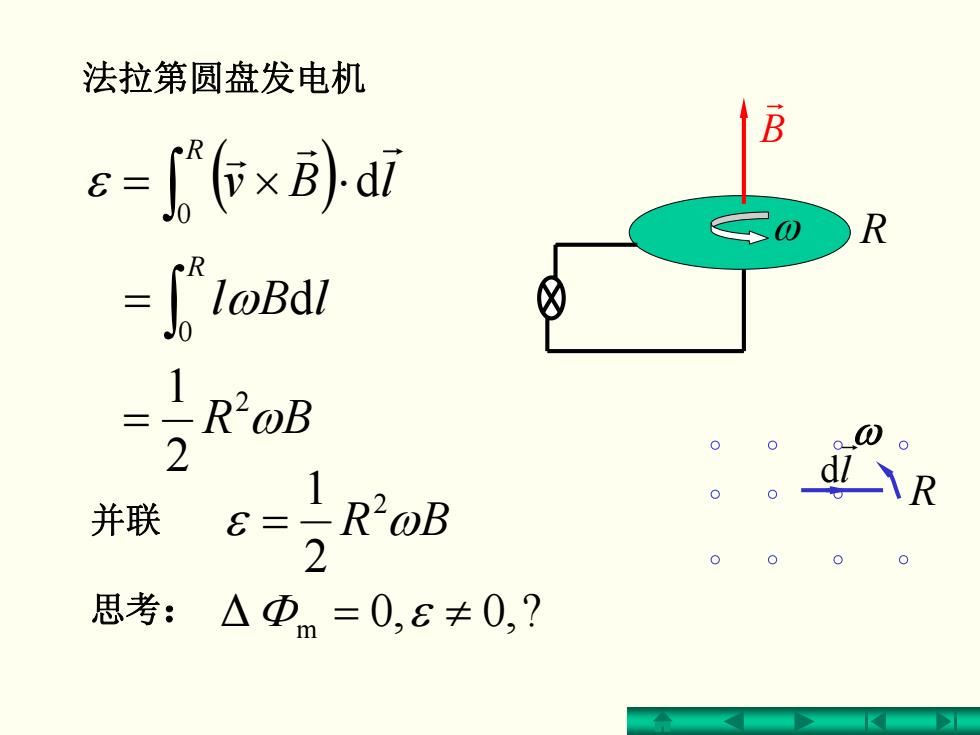
法拉第圆盘发电机 B s=作×dd R -ftohar 2 并联 8= R2oB 2 思考:△①m=0,6≠0,?
法拉第圆盘发电机 ( ) ∫ ⋅×= R lBv 0 d r r r ε r B ω R ∫ = R lBl 0 ω d ωBR2 2 1 = 并联 ωε BR2 2 1 = Δ ?,0,0 思考 : Φ m = ε ≠ ω R l r d