
第16章变化的电磁场 §16.1电磁感应定律 §16.2动生电动势 §16.3感生电动势 感应电场 §16.4自感和互感 §16.5电容和电感电路中的暂态电流 §16.6磁场能量 §16.7位移电流 §16.8麦克斯韦电磁场方程组
第 16 章 变化的电磁场 §16.2 动生电动势 §16.1 电磁感应定律 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组 §16.5 电容和电感电路中的暂态电流
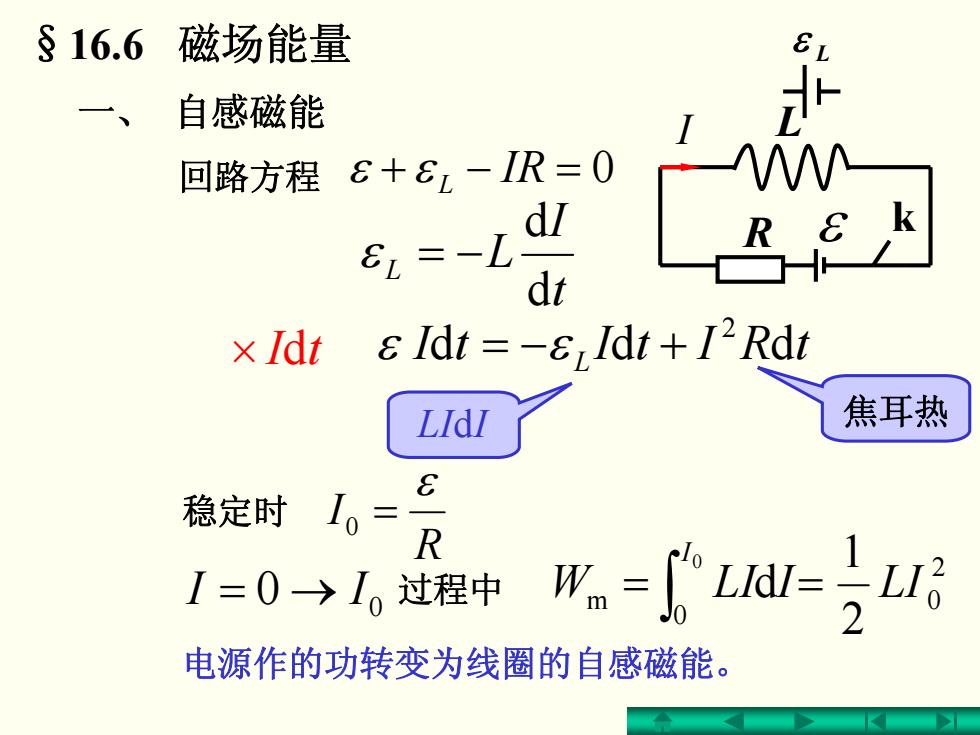
§16.6 磁场能量 自感磁能 回路方程 ε+L-IR=0 dl 8L=-L dt x Idt εldt=-&Idt+I2Rdt LIdI 焦耳热 E 稳定时 10= R I=0>I,过程中 =i=2g 电源作的功转变为线圈的自感磁能
§16.6 磁场能量 一、 自感磁能 稳定时 R I ε 0 = tRItItI L ddd 2 εε +−= ∫ = 0 0 m d I ILIW 20 21 = LI L R ε k × dtI L ε ε + ε L − IR = 0 t I L L dd ε −= dILI 焦耳热 I 回路方程 0 0 →= II 过程中 电源作的功转变为线圈的自感磁能

以密绕长直螺线管为例(长:1,横截面积:S,体积:V) NIo N2S :B=μ1 L=μ1 Wm= 1 N2S B2 21 1B2 (SY) 磁场能量密度 2 u 24 2 一餐情视承-小d=)6 Wm= BH 2 计算自感的又一种方法:B→W→L= 2Wm
以密绕长直螺线管为例 ( 长: l, 横截面积: S, 体积: V ) l SN L l NI B 2 0 Q = μ = μ 22 2 2 2 m 0 )( 2 1 2 1 l N B l SN LIW μ == μ V B Sl B μ μ 2 2 2 1 )( 2 1 = = ∫∫∫ m = m dVwW BHV 2 1 = 2 0 2 1 = LI 2 m m 2 I W LWB =→→ r BHw 2 1 m = 磁场能量密度 一般情况 计算自感的又一种方法:
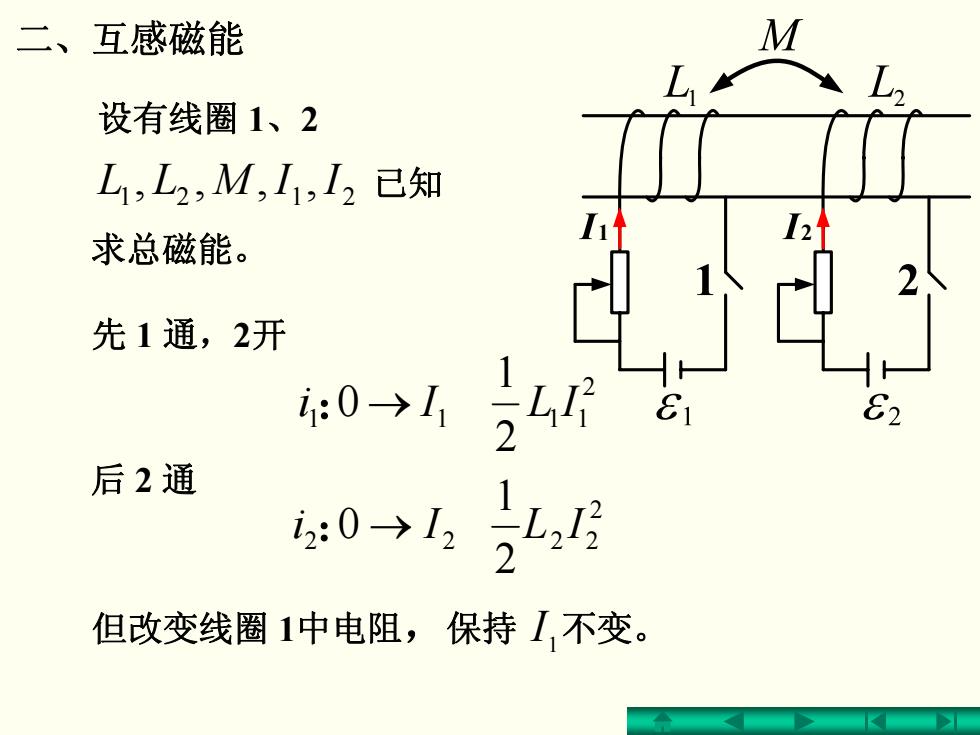
二、互感磁能 设有线圈1、2 L1,L2,M,I1,I2已知 求总磁能。 先1通,2开 :0→1 81 后2通 i2:0→12 但改变线圈1中电阻,保持I,不变
二、互感磁能 2 1 111 2 1 : → 0 ILIi 先 1 通,2开 后 2 通 2 2 222 2 1 : → 0 ILIi 但改变线圈 1中电阻,保持 不变。 1 I 设有线圈 1、2 2121 ,,,, IIMLL 求总磁能。 已知 1 2 1 2
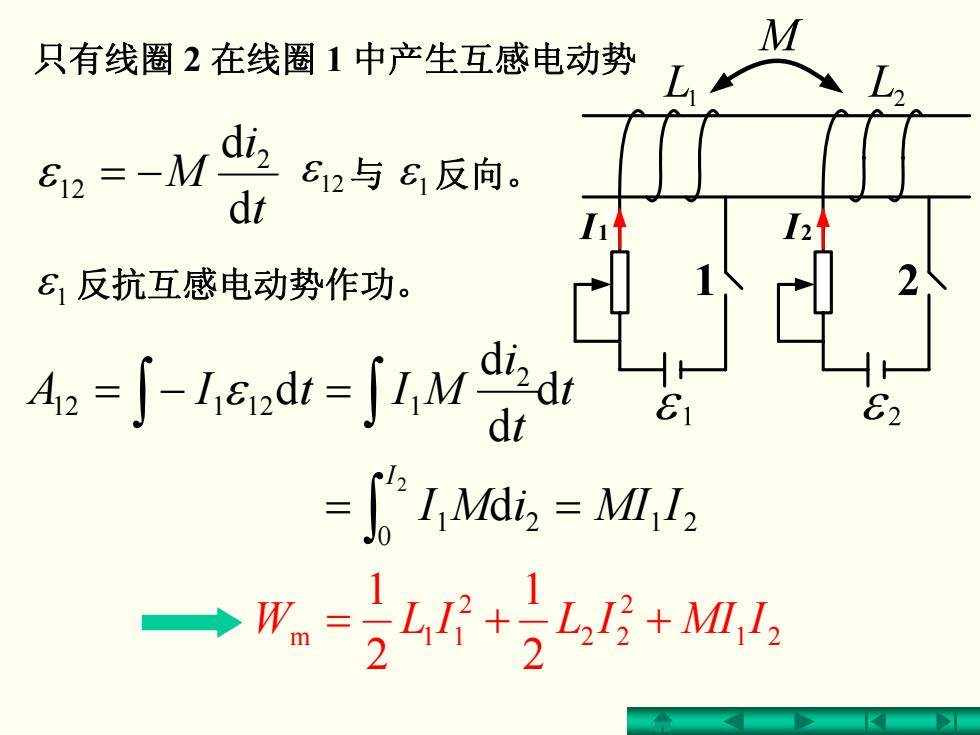
M 只有线圈2在线圈1中产生互感电动势 E12=-M 812与61反向。 dt 8反抗互感电动势作功。 A:-「-1a=j =1,M,=M,12 →顶=4+4g+M4
1 2 1 2 t t i MItIA d d d d 2 12 121 =−= ∫∫ 1 ε t i M d d 2 ε 12 −= ε 12与 ε 1反向。 21 2 22 2 m 11 2 1 2 1 ++= IMIILILW 只有线圈 2 在线圈 1 中产生互感电动势 ε 1 反抗互感电动势作功。 212 0 1 d 2 IMIiMI I = = ∫

设11,12 产生磁场B,B2,i,H2 B=B+B, 形。小∬.r =3ja,+庄,a,+,r 2jH+H+2A·A,r
设 21 , II 产生磁场 2121 , , , HHBB r r r r 21 HHHBBB 21 r r r r r r +=+= ∫∫∫ W ⋅= dVHB 21 m r r ( ) ∫∫∫ = ⋅++ d2 VHHHH 21 21 22 21 r r μ ( )( )dVHHHH 21 2121 r r r r = +⋅+ ∫∫∫ μ

[例16-10] 如图同轴电缆,已知,乃2,1,I,4 求磁场能量及自感。 解:H= B= r<r<2 2元r 2元r Wm= BH= 2 2 8π2r2 n=wn2ldr=M2in 4元 2元 END
[例16-10] 如图同轴电缆,已知 21 Ilrr , , , , μ 求磁场能量及自感。 1 2 2π 2π rrr r I B r I H <<== μ 解: 22 2 m 82 π 1 r I BHw μ == ∫ = 21 2π d m m rr rrlwW 1 2 2 ln 4π r μ rlI = 1 2 2 2 m m ln 2π 2 21 rrl IW LLIW μ Q ==∴= 1r 2r I I END