
第16章变化的电兹场 §16.1电磁感应定律 §16.2动生电动势 §16.3感生电动势 感应电场 §16.4自感和互感 §16.5电容和电感电路中的暂态电流 §16.6磁场能量 §16.7位移电流 §16.8麦克斯韦电磁场方程组
第 16 章 变化的电磁场 §16.2 动生电动势 §16.1 电磁感应定律 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组 §16.5 电容和电感电路中的暂态电流

§16.3感生电动势 感应电场 一、感生电动势 dΦ. I变化时8= I= dt R 产生感生电动势的 非静电力是什么? F=q(E+立×B) B() 1.可=0,B=0→fm=02. ilg 产生感生电动势的非静电力一定不是洛仑兹力
§16.3 感生电动势 感应电场 一、 感生电动势 dt dΦ m ε −= R I ε i = BvEqF )( r r r r ×+= tB )( r F r q 2. 产生感生电动势的非静电力一定不是洛仑兹力。 I l 产生感生电动势的 Ii 非静电力是什么? 00,0 fBv m =⇒== r r r 1. I 变化时

麦克斯韦提出感应电场概念:当空间中的磁场 发生变化时,就在周围空间激起感应电场E, 在导体中产生感生电动势,并形成感应电流。 -段号线:8=心兵d闭合回路:8-5瓦d0 d7= dm dt a=儿0 dt →f瓜d成=瓜酒安生场
t lE l d d d m i Φ −=⋅ ∫ r r ∫∫∫∫ ⋅=⋅= S S S tB SB tt r r r r d d d d d d m ∂ Φ ∂ ∫ ⋅= l lEr r d i ε ∫∫∫ ⋅−=⋅⇒ l S S tB lE r r r r i d d ∂ ∂ 麦克斯韦提出感应电场概念:当空间中的磁场 发生变化时,就在周围空间激起感应电场 , 在导体中产生感生电动势,并形成感应电流。 Ei r 一段导线: 闭合回路: 变化磁场产生电场! ∫ ⋅= ba lEr r ε i d

二、感应电场的性质 静电场 E 感应电场 E 场源 静电荷 变化的磁场 环流 fE、di=0 d .dS 静电场为无旋场! 感应电场为有旋场! 通量 d5 乐E,d=0 静电场为有源场! 感应电场为无源场!
静电场 Es r 感应电场 Ei r 场源 静电荷 变化的磁场 环流 S =⋅ 0d ∫l lEr r ∫∫∫ ⋅−=⋅ l S S tB lE r r r r d d i ∂ ∂ 通量 0 s d ε q SES =⋅ ∫∫ r r 0d i =⋅ ∫∫S SEr r 二、感应电场的性质 静电场为无旋场! 感应电场为有旋场! 静电场为有源场! 感应电场为无源场!
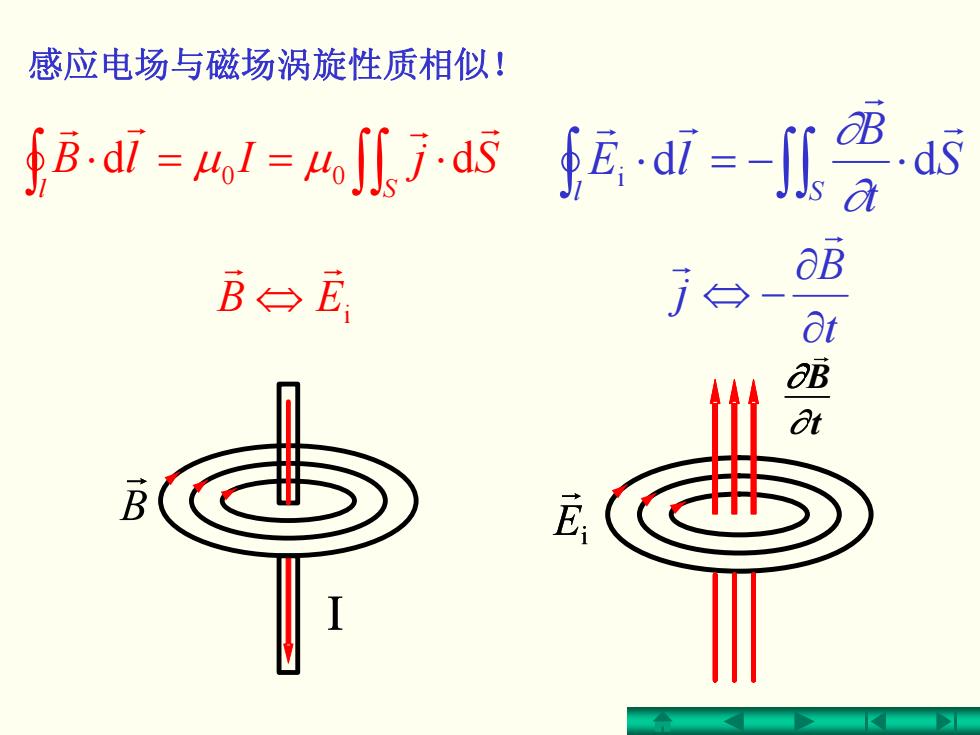
感应电场与磁场涡旋性质相似! .ds B⊙E aB at B E
∫ ∫∫ ⋅==⋅ l S SjIlBr r r r d μμ 00 d ∫∫∫ ⋅−=⋅ l S S tB lE r r r r i d d ∂ ∂ EB i r r ⇔ t B j ∂∂ −⇔ r r t B 感应电场与磁场涡旋性质相似!
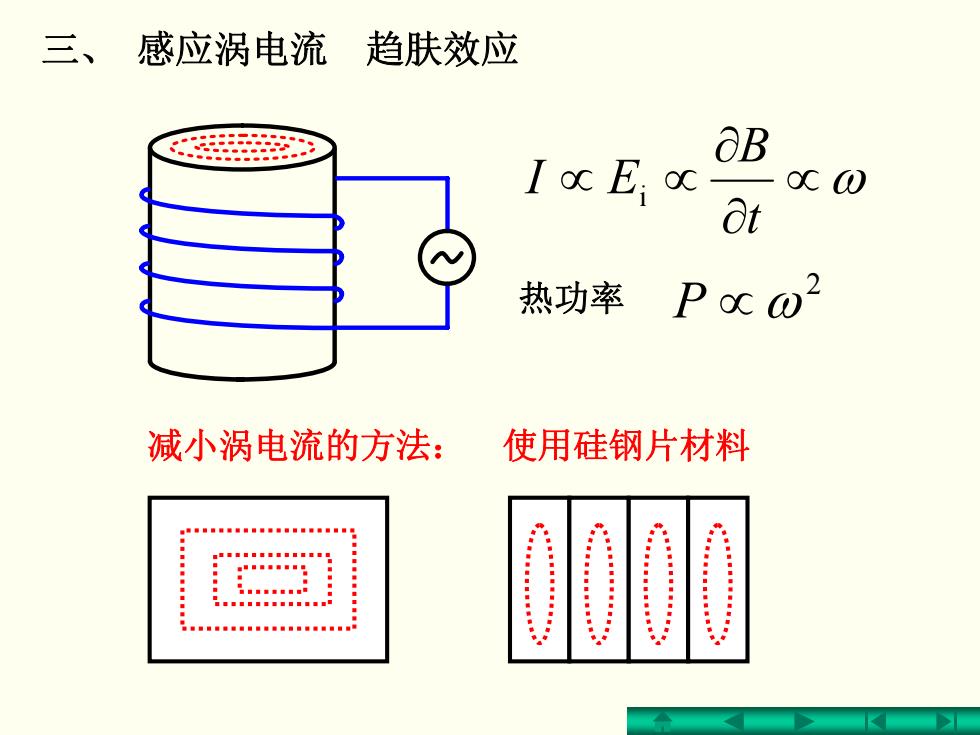
三、感应涡电流 趋肤效应 6B I o E oc W 8t 热功率 c02 P 减小涡电流的方法: 使用硅钢片材料 。。。。。。 AnEEEEnEnMaai MMNAMAMNNMAMANMMMnaaM
∝ ω ∂ ∂ ∝∝ t B EI i 减小涡电流的方法: 使用硅钢片材料 三、 感应涡电流 趋肤效应 2 热功率 P ∝ ω
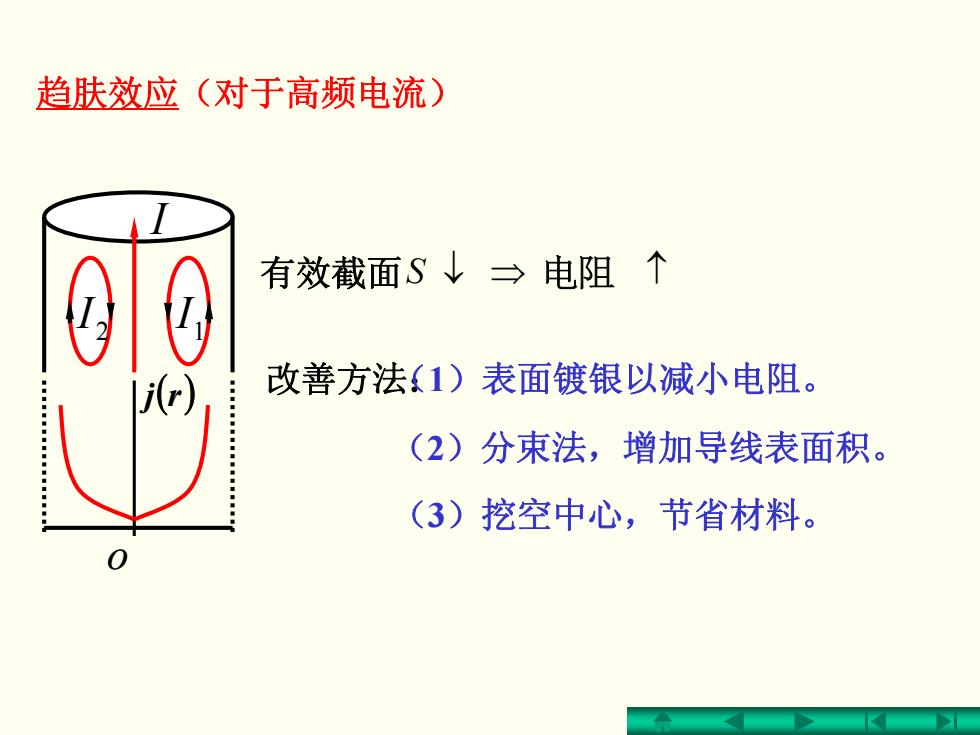
趋肤效应(对于高频电流) 有效截面S↓→电阻个 jr) 改善方法(1)表面镀银以减小电阻。 (2)分束法,增加导线表面积。 (3)挖空中心,节省材料
趋肤效应(对于高频电流) I ( )rj o 有效截面S 电阻 ↑⇒↓ 改善方法:(1)表面镀银以减小电阻。 (2)分束法,增加导线表面积。 (3)挖空中心,节省材料。 1I 2 I

四、感生电动势的计算 1.导体为闭合回路 dΦ 2.非闭合回路 dt (1) f病a-心 .dS →E,→e=Edl (2)8= dm=8oc+6ca dt →Eabc=e-8cda
四、感生电动势的计算 2. 非闭合回路 1. 导体为闭合回路 d t d Φ m ε −= a b c d abc cda ⇒ ε = ε − ε ∫∫∫ ⋅−=⋅ l S S t B lE r r r r i d d ∂ ∂ ( 1 ) abc cda t εε Φ ε +=−= d d m ( 2 ) Ei r ⇒ ∫ ⋅=⇒ c a lEr r d i ε

若既有动生电动势,又有感生电动势 c=心6xB)d7+心E,dl 或: G=f6x卧-儿西s
若既有动生电动势,又有感生电动势 ( ) ∫∫ ⋅+⋅×= b a b a lElBv r r r r r ε d i d 或: ( ) ∫∫∫ ⋅−⋅×= l S S t B lBv r r r r r d d ∂ ∂ ε
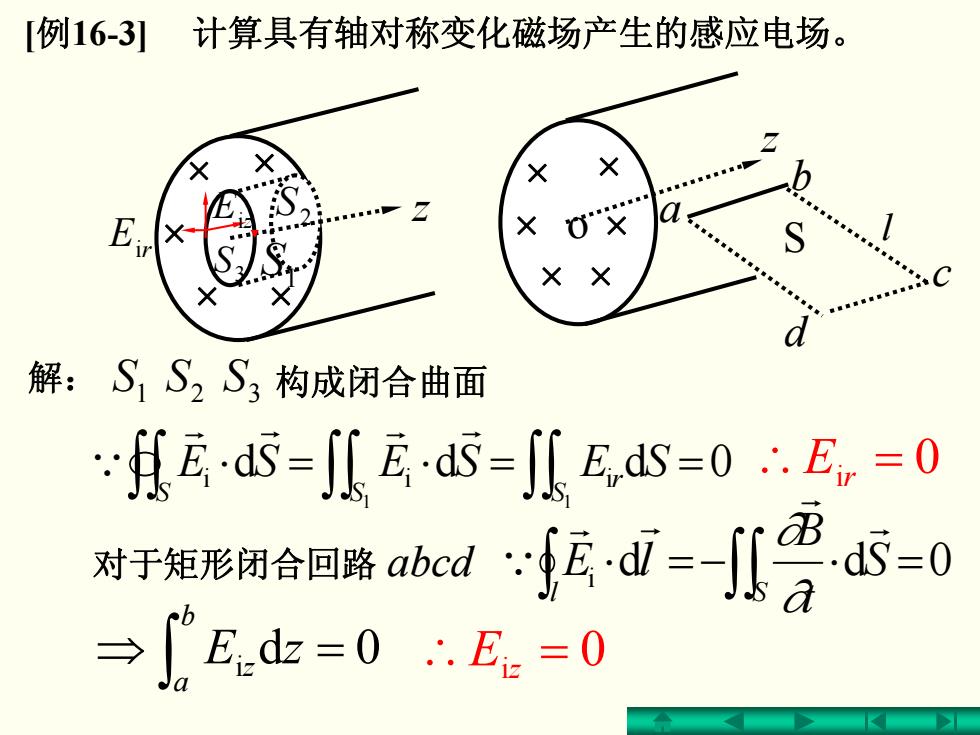
[例16-3) 计算具有轴对称变化磁场产生的感应电场。 解:S,S2S3构成闭合曲面 其Eds=瓜Eas=八6,ds=0E=0 对于矩形闭合同路acd在d=心d5=0 →E=0∴E。=0
0ddd 1 1 i i i ==⋅=⋅ ∫∫∫∫∫∫ S r S S SESESEr r r r Q ∴ Ei r = 0 d 0d i =⋅−=⋅ l ∫∫∫ S S t B lE r r r r Q ∂ ∂ i =⇒ 0d ∴ Ei z = 0 ∫ b a z zE 解: S 1 S 2 3 S 构成闭合曲面 [ 例16-3] 计算具有轴对称变化磁场产生的感应电场。 对于矩形闭合回路 abcd z 1 S S 2 S 3 Eir × × × × × o a b c d z S × × × × l Eiz × ×