
第17章机械波 §17.1机械波的类型 §17.2机械波的速度 §17.3惠更斯原理 §17.4平面简谐波 §17.5平面波的波动方程 §17.6波的能流密度和强度 §17.7半波反射和全波反射 §17.8波的叠加和干涉现象 §17.9多普勒效应
第 17 章 机械波 §17.1 机械波的类型 §17.2 机械波的速度 §17.3 惠更斯原理 §17.4 平面简谐波 §17.5 平面波的波动方程 §17.6 波的能流密度和强度 §17.7 半波反射和全波反射 §17.8 波的叠加和干涉现象 §17.9 多普勒效应

§17.8波的叠加和干涉现象 一、波的叠加原理 1.波传播的独立性原理:若干列波在传播过程中相 遇,每列波仍将保持其原有的振动特性(频率,波 长,振幅,振动方向),不受其它波的影响。 2.波的叠加原理:在相遇区域内,任一质元振动的位 移是各列波单独存在时在该点引起的位移的矢量和
一、波的叠加原理 1. 波传播的独立性原理:若干列波在传播过程中相 遇,每列波仍将保持其原有的振动特性(频率,波 长,振幅,振动方向),不受其它波的影响。 2. 波的叠加原理:在相遇区域内,任一质元振动的位 移是各列波单独存在时在该点引起的位移的矢量和。 §17.8 波的叠加和干涉现象

振动叠加发生在单一质点元 波的叠加发生在波的相叠区域 波动方程的线性决定了波服从叠加原理 波的强度过大(如冲击波)→非线性波 →叠加原理不成立。 ★电磁波 麦克斯韦方程组的四 个方程都是线性的, 解满足叠加原理。 光波在媒质中传播时 弱光媒质可看作线性媒质。 强光媒质非线性,波的叠加原理不成立
振动叠加发生在单一质点元 波的叠加发生在波的相叠区域 波动方程的线性决定了波服从叠加原理 波的强度过大(如冲击波) →非线性波 →叠加原理不成立。 ★电磁波 麦克斯韦方程组的四 个方程都是线性的, 光波在媒质中传播时 弱光 媒质可看作线性媒质。 强光 媒质非线性, 波的叠加原理不成立。 ——解满足叠加原理
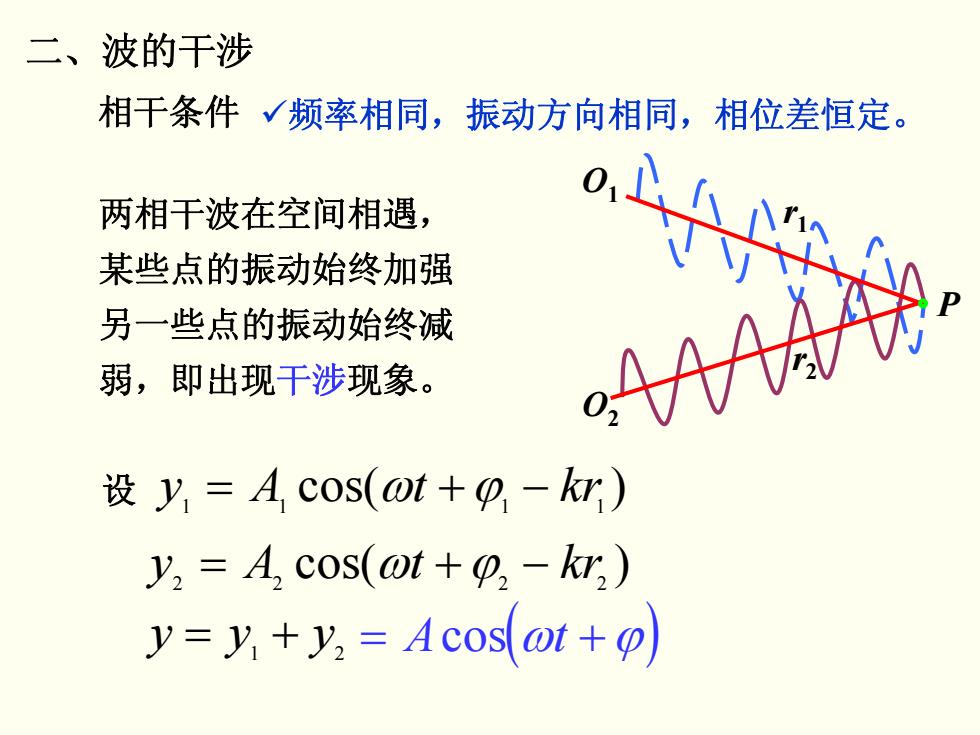
二、波的干涉 相干条件√频率相同,振动方向相同,相位差恒定。 两相干波在空间相遇, 某些点的振动始终加强 另一些点的振动始终减 弱,即出现干涉现象。 设y=A,Cos(ot+0-) y2=A2c0s(0t+0,-kw,) y=y+y:=Acosot+o)
二、波的干涉 相干条件 9频率相同,振动方向相同,相位差恒定。 两相干波在空间相遇, 某些点的振动始终加强 另一些点的振动始终减 弱,即出现干涉现象。 设 y A t kr 1 1 = cos( ) ω +ϕ1 1 − y A t kr 2 2 = cos( ) ω +ϕ2 2 − yy y = 1 2 + = + A t cos(ω ϕ) P r2 r1 O1 O2

其中A=A+A+2AA,c0S△0 △0=0-0,-k(g- 设 %=g0=:-)2牙-r) >当3-=士n2,n=0,1,2,… A=A+AI=1,+1+2V1,1相长 当5-片=±2m+0,n=0,12, A=A-A1=1,+1,-2VI1, 相消
A A A AA 2 1 2 2 2 = + + 2 1 2 cos Δϕ Δϕϕϕ =−− − 1 2 12 kr r ( ) 其中 设 ϕ2 1 = ϕ ( ) ( ) 12 12 2 π −=−=Δ rrrrk λ ϕ ¾ 当 − 12 = ± λ nnrr = ,2,1,0 , L A A A I I I II = + =++ 1 2 1 2 12 2 ¾ 当 ( ) ,2,1,0 , L 2 12 12 nnrr =+±=− λ A A A I I I II = − =+− 1 2 1 2 12 2 相长 相消

[例17-7 两相干机械波,振源相位差为的奇数倍, 在P点相遇,若波程差为半波长的偶数倍, 问P点是加强还是减弱? 解: A0=0-9,-k(-5) 0,-p2=(2k+1F-y=2n2 ag=bt+咖-变d-+1-2n 振动减弱
[例17-7] 两相干机械波,振源相位差为π的奇数倍, 在P点相遇,若波程差为半波长的偶数倍, 问P点是加强还是减弱? 解: Δϕϕϕ =−− − 1 2 12 kr r ( ) ϕ −ϕ21 = ( k +12 )π rr n 1 2 2 2 −= ⋅ λ ( ) ( ) 212 π 2π ∴ k 12 π λ −+=−+=Δ nkn λ ϕ 振动减弱

初相相同振幅相同,PQ= 3 [例17-8两相干波源P、Q, 2 R为PQ连线上任一点,求R点振动的振幅。 P R 解: △p=0-9,-k-5) =-k九=-3元 减弱 A=
[例17-8]两相干波源P、Q,初相相同振幅相同, λ 2 3 PQ = R为PQ连线上任一点,求R点振动的振幅。 P QR 3 2 λ 解: Δϕϕϕ =−− − 1 2 12 kr r ( ) 3π 2 3 k λ −=−= 减弱 A = 0

[例17-9]A、B分别为两个相干平面简谐波的波源,振幅均为 5cm,频率为100Hz,波速为10m/s。A点为波峰时,B点恰 为波谷,试确定两列波在P点干涉的结果。 解:BP=√202+152=25m 元=-4=0.1m 15m A 20m B 设A比B超前π PA一PB=元 BP-AP 25-15 △p=pB-0A-2元 =-元-2元 0.1 =-201元反相位 A=0 P点静止!
[例17-9]A、B分别为两个相干平面简谐波的波源,振幅均为 5cm,频率为100Hz,波速为10m/s。A点为波峰时,B点恰 为波谷,试确定两列波在P点干涉的结果。 解: 15m A B P 20m m251520 22 BP =+= == m1.0 ν λ u 设A比B超前π ϕ −ϕ BA = π 1.0 1525 2π π 2π − −−= − −−=Δ λ ϕϕϕ APBP AB = −201π 反相位 A = 0 P点静止!

[例17-10]两相干波源S,和S,的间距为d=30m,且都在x轴上, S,位于原点0。设由两波源分别发出两列波沿x轴传播,强度 保持不变。x1=9m和x2=12m处的两点是相邻的两个因干涉 而静止的点。求两波长和两波源间最小相位差。 S x1 x2 S2 d X 解:设S,和S,的振动相位分别为: 01 P2 飞点的振动相位差: aa牙d-x1-a牙x=2+ 2元
[例17-10]两相干波源S1和S2的间距为d=30m,且都在x轴上, S1位于原点o。设由两波源分别发出两列波沿x 轴传播,强度 保持不变。x1 =9m和 x2=12m处的两点是相邻的两个因干涉 而静止的点。求两波长和两波源间最小相位差。 解: o S1 x S2 1 x2 d x 设S1和S2的振动相位分别为:ϕ1 ϕ 2 )12(] π 2π [)]( 2π [ 2 xd 1 1 1 kx +=−−−− λ ϕ λ (1) ϕ x1点的振动相位差:

飞2点的振动相位差: [p2 2π(d-x,】-9-元 πx,1=(2k+3m (2) 4(x2-x)=2m 元=2(x2-x)=2(12-9)=6m 由(1)式02-0,=(2k+1)元 2m(d-2x) =(2k+5)π =-2,一3时相位差最小 P2-01=士π S X1 x2 S, d
)32(] π 2π [)]( 2π [ 2 xd 2 1 2 kx +=−−−− λ ϕ λ ϕ x2点的振动相位差: (2) 2)( π 4π xx 12 =− λ λ = − xx 12 = − = m6)912(2)(2 由(1)式 )2( 2π 12 )12( π 1 k −++=− xd λ ϕϕ = k + )52( π k= -2,-3时相位差最小 ϕ −ϕ12 = ±π o S1 x S2 1 x2 d x