
第20章光的干涉和衍射 §20.1光波的相干叠加 §20.2双缝干涉 §20.3薄膜干涉 §20.4偏振光的干涉 §20.5光的衍射 §20.6光栅衍射 §20.7圆孔衍射光学仪器的分辨本领 §20.8X射线的衍射
§20.1 光波的相干叠加 §20.3 薄膜干涉 §20.4 偏振光的干涉 §20.5 光的衍射 §20.6 光栅衍射 §20.7 圆孔衍射 光学仪器的分辨本领 §20.8 X射线的衍射 第 20 章 光的干涉和衍射 §20.2 双缝干涉
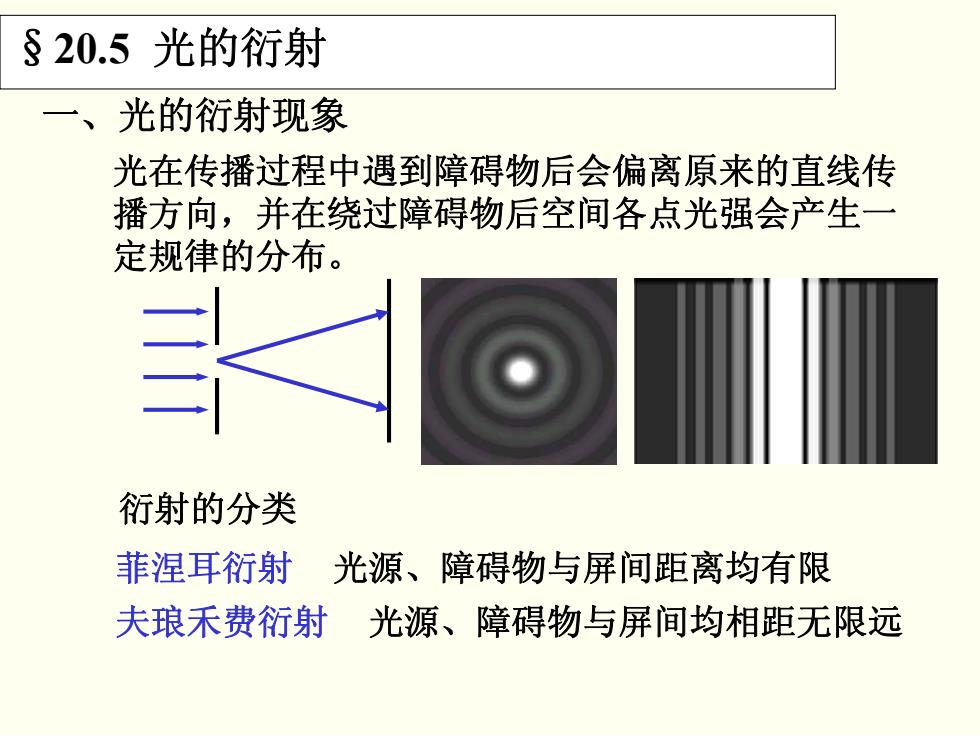
§20.5光的衍射 一、光的衍射现象 光在传播过程中遇到障碍物后会偏离原来的直线传 播方向,并在绕过障碍物后空间各点光强会产生一 定规律的分布。 } 衍射的分类 菲涅耳衍射光源、障碍物与屏间距离均有限 夫琅禾费衍射 光源、障碍物与屏间均相距无限远
一、光的衍射现象 §20.5 光的衍射 光在传播过程中遇到障碍物后会偏离原来的直线传 播方向,并在绕过障碍物后空间各点光强会产生一 定规律的分布。 衍射的分类 夫琅禾费衍射 光源、障碍物与屏间均相距无限远 菲涅耳衍射 光源、障碍物与屏间距离均有限

二、惠更斯一菲涅尔原理 在任一时刻,波阵面上每一未被阻挡的点均起着次 级球面子波波源的作用,障碍物后任一点上光场的 振幅是所有这些子波源所发出的球面子波的叠加。 数学表示: 理想单色光波的波动表达式 E(r,t)=A(r)cos @t-p(r) 复数表示 E(rt)=4(r)eil-0)1=A(r)e(e-ior 复振幅 w(r)=A(r)eio(r) 光强I=w(r)w(r) 辐角0(r)一相位在空间的分布
二、惠更斯—菲涅尔原理 在任一时刻,波阵面上每一未被阻挡的点均起着次 级球面子波波源的作用,障碍物后任一点上光场的 振幅是所有这些子波源所发出的球面子波的叠加。 数学表示: 理想单色光波的波动表达式 = [ω −ϕ rtrAtrE )(cos)(),( ] 复数表示: [ rti ] tiri rAr,tE rA −− ϕω − ωϕ = e)()( = ee)( ~ )( )( 复振幅 )( e)()( ri rAr ϕ ψ = 辐角ϕ r)( —— 相位在空间的分布 光强 )()( * ⋅= ψψ rrI
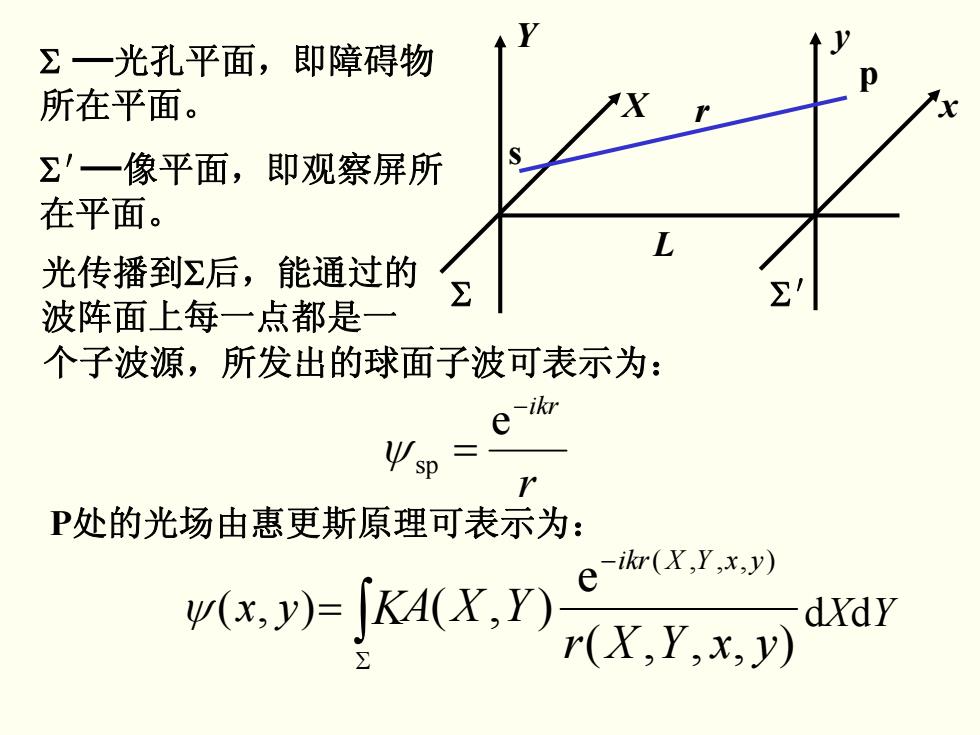
Σ一光孔平面,即障碍物 所在平面。 Σ'一像平面,即观察屏所 在平面。 光传播到Σ后,能通过的 波阵面上每一点都是一 个子波源,所发出的球面子波可表示为: Ψp= P处的光场由惠更斯原理可表示为: 小KX, -ikr(XY,x,y) dXdY
r −ikr = e ψ sp P处的光场由惠更斯原理可表示为: ψ yx ),( ),,,( e ),( ),,,( yxYXr YXA − yxYXikr ∫ Σ = K dd YX Y X y x s p L r Σ Σ′ Σ 光孔平面,即障碍物 所在平面。 Σ′ 像平面,即观察屏所 在平面。 光传播到 Σ后,能通过的 波阵面上每一点都是一 个子波源,所发出的球面子波可表示为:
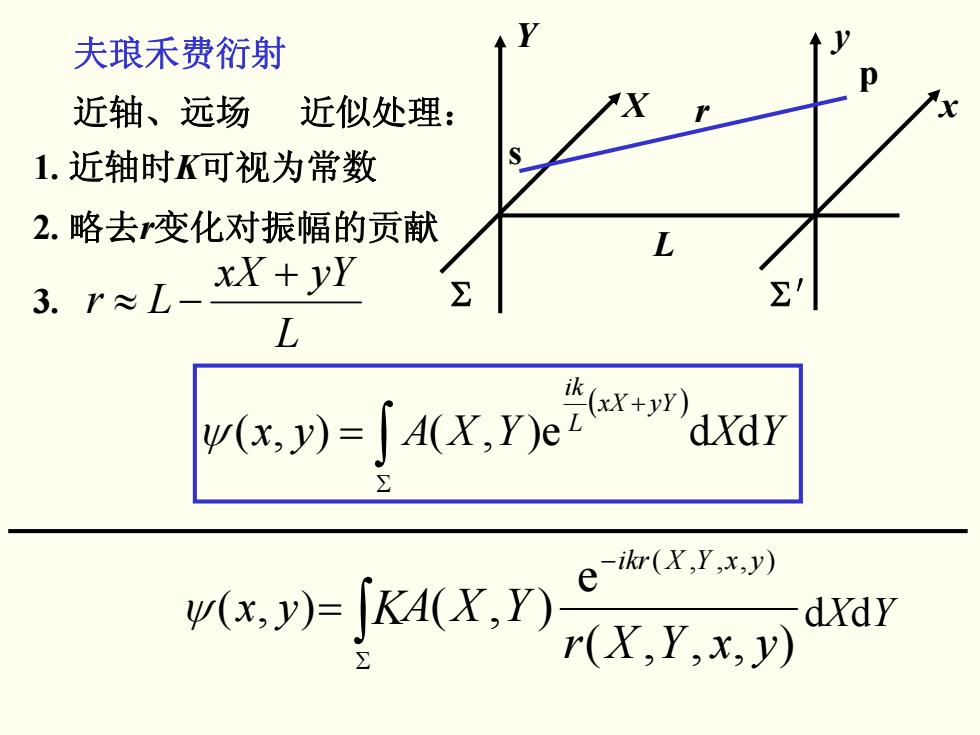
夫琅禾费衍射 近轴、远场 近似处理: 1.近轴时K可视为常数 2.略去变化对振幅的贡献 3.r≈L- xX+yY L k,y-jd〔X,reaa ∑ =[KACX,Y) h(X,y,)) (X.Y.x.y) dXdY
夫琅禾费衍射 近轴、远场 近似处理: 1. 近轴时K可视为常数 2. 略去r变化对振幅的贡献 3. L yYxX Lr + −≈ ( ) ∫ Σ + = YXAyx YX yYxX Lik ψ dde),(),( Y X y x s p L r Σ Σ′ ψ yx ),( ),,,(e ),( ),,,( yxYXr YXA − yxYXikr ∫Σ = K dd YX
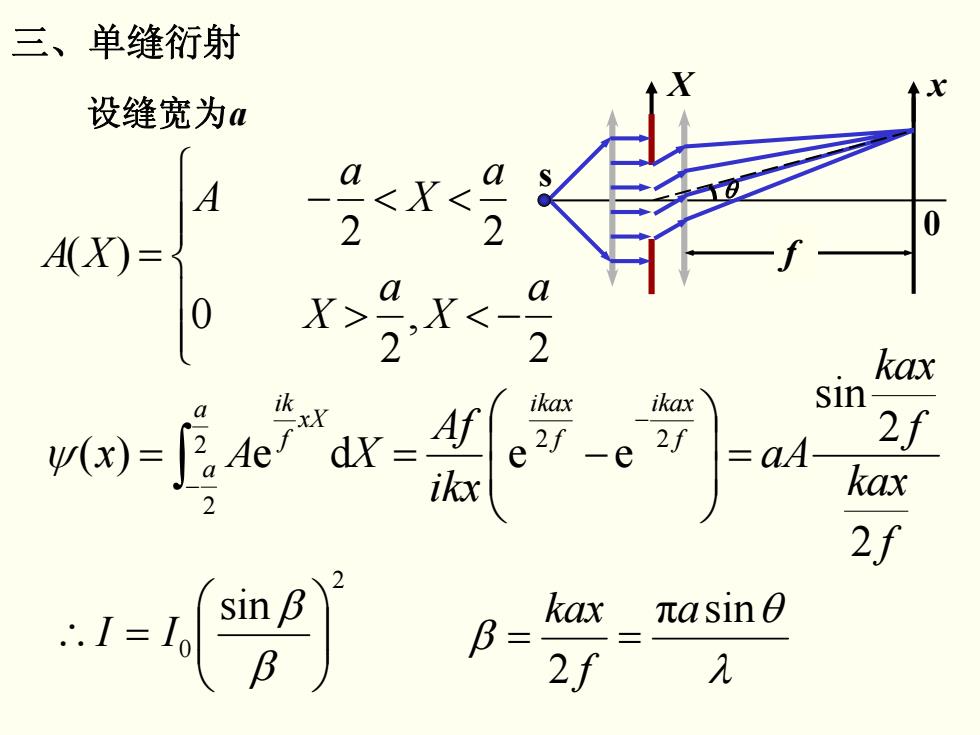
三、单缝衍射 设缝宽为a A 2 A(X)= 0 X 2 2 kax ik ikax kax dr- e 2f aA kx e kax 2f kax ,πasin O B 2f 几
三、单缝衍射 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ −<> <<− = 2 , 2 0 22 )( a X a X a X a A XA f kax f kax aA ikx Af XAx f ikax f a ikax a xX f ik 2 2 sin eede)( 2 2 2 2 =⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = −= − −∫ ψ 2 0 sin ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ =∴ β β II X x f 0 s θ 设缝宽为 a λ θ β π sin 2 a f kax ==

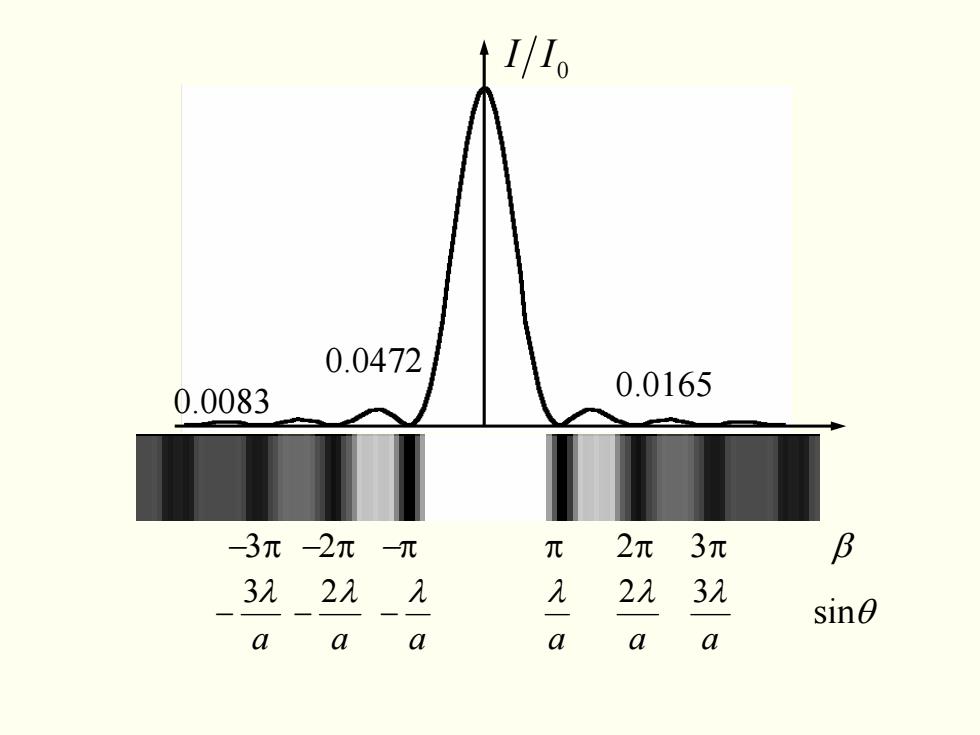
光强分布 暗纹:当sinB=0(即B=士kπ,k=1,2,..时),I=0 → asin0=±k2 明纹:当B=0时,I-Imax=1,中央明条纹 由 d=0→tanB=B,B=±1.43m,±2.46m,±3.47m,… dB 其他明纹位置满足asin0=±1.432,±2.46,±3.47元,. 光强:10,0.04721,0.0165,0.0083L,…即1其它<1中央 .1=0 kax nasinO 2f λ
光强分布 当sinβ = 0(即β = ±kπ ,k =1,2,…时),I = 0 asinθ = ±kλ 暗纹: 明纹:当β = 0 时,I = Imax= I0 中央明条纹 由 0 dd = βI β = β,tan 其他明纹位置满足 β = ± 43.1 ,± 2.46ππ ,± 3.47π,… a θ = ± λ ± λ ± λ,47.3 ,46.2 ,43.1sin … 光强:I0,0.0472I0, 0.0165I0, 0.0083I0,… 即I其它<< I中央 2 0 sin ⎟⎟⎠⎞ ⎜⎜⎝⎛ =∴ ββ II λ θ β π sin 2 a f kax ==
↑I/1o 0.0472 0.0083 0.0165 -3π-2元-π 元 2元3元 B 322九元 2λ 3λ sin0 aa a 2-a a a
−3π −2π −π π 2π 3π β sinθ a λ a 2λ a 3λ a λ − a 2λ − a 3λ − 0 II 0.0472 0.0165 0.0083
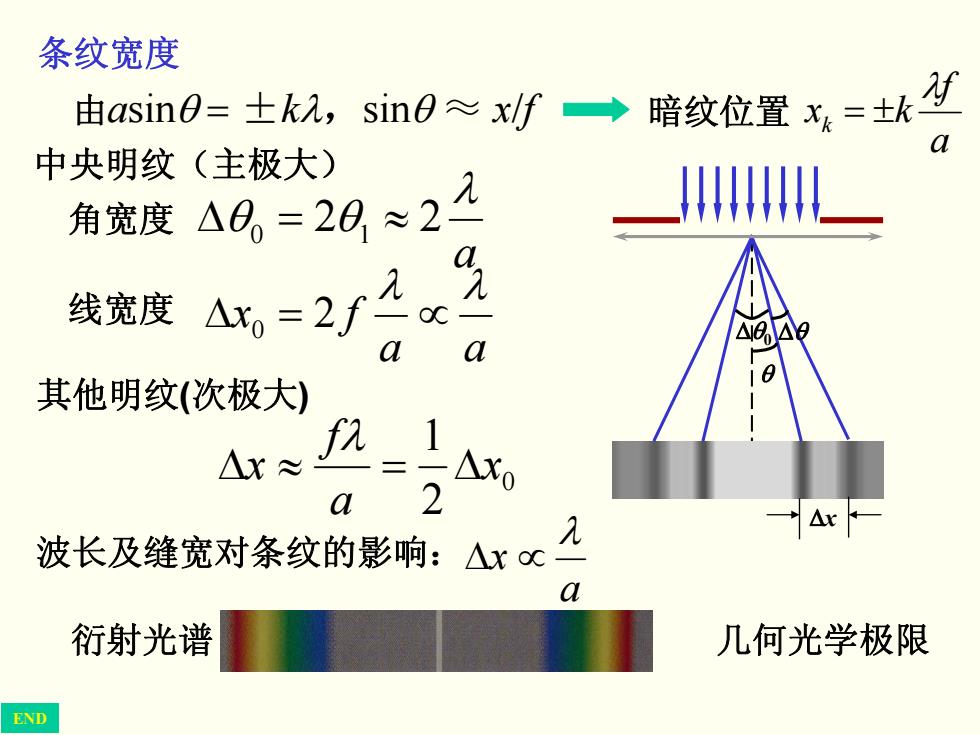
条纹宽度 由asin0=±kλ,sin0≈x/f◆ 暗纹位置x=士k a 中央明纹(主极大) 角宽度48,=2日≈22 _W 线宽度 a 其他明纹(次极大) 4r1 2 △ 波长及缝宽对条纹的影响:△xoc a 衍射光谱 几何光学极限 END
条纹宽度 由asinθ = ±kλ,sinθ ≈ x/f a f kxk λ 暗纹位置 ±= 角宽度 a λ θθ 22 10 ≈=Δ 线宽度 aa fx λ λ 0 2 ∝=Δ 中央明纹(主极大) 其他明纹(次极大) 0 2 1 x a f x Δ=≈Δ λ 波长及缝宽对条纹的影响: a x λ ∝Δ 衍射光谱 几何光学极限 Δθ0 Δθ θ Δx END