非线性物理:元胞自动机 简单系统模拟:砂堆规则 应颗粒物质研究的重要性而诞生。可以用简单的元胞自动机进行 处理,却能够漂亮地显示实际砂堆坍塌过程。 针对正方网格,根据微观规则进行模拟。一般情况下,借助 Moore八邻居规则足够,运动冲突情况下使用Margolusi规则
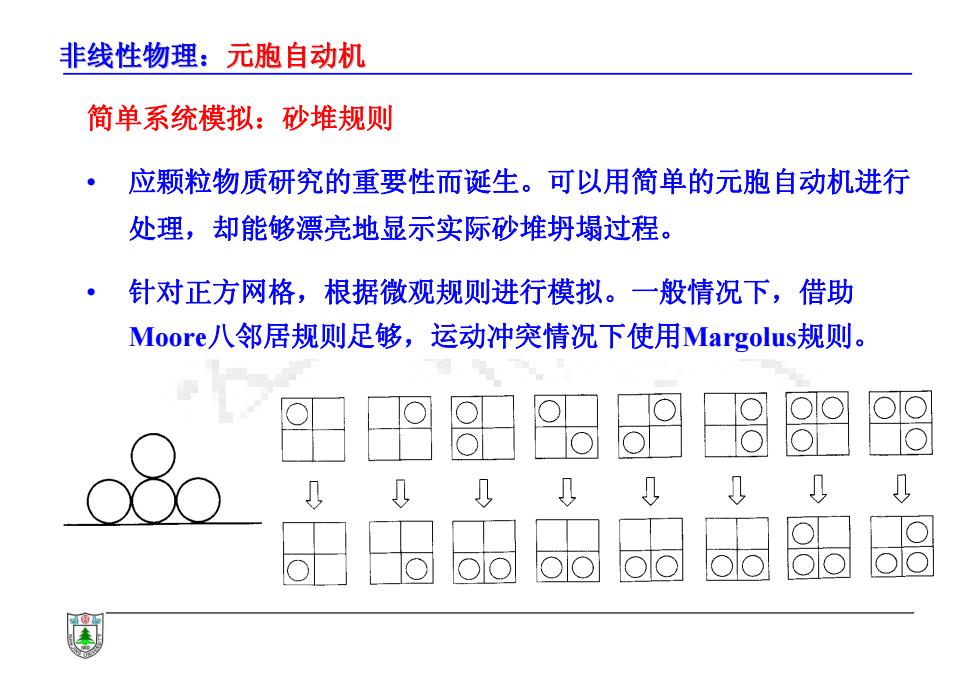
非线性物理:元胞自动机 简单系统模拟:砂堆规则 • 应颗粒物质研究的重要性而诞生。可以用简单的元胞自动机进行 处理,却能够漂亮地显示实际砂堆坍塌过程。 • 针对正方网格,根据微观规则进行模拟。一般情况下,借助 Moore八邻居规则足够,运动冲突情况下使用Margolus规则
非线性物理:元胞自动机 可见,砂堆规则分成确定性规则和概率规则两类,需要对实际微 观事件进行仔细考虑。 假定不出现上述右侧的阻塞行为,砂堆过程可以进行数学处理。 假定同步更新前后状态,则(up-low-left-right): Su什)=SuSulSi+I-SSu/
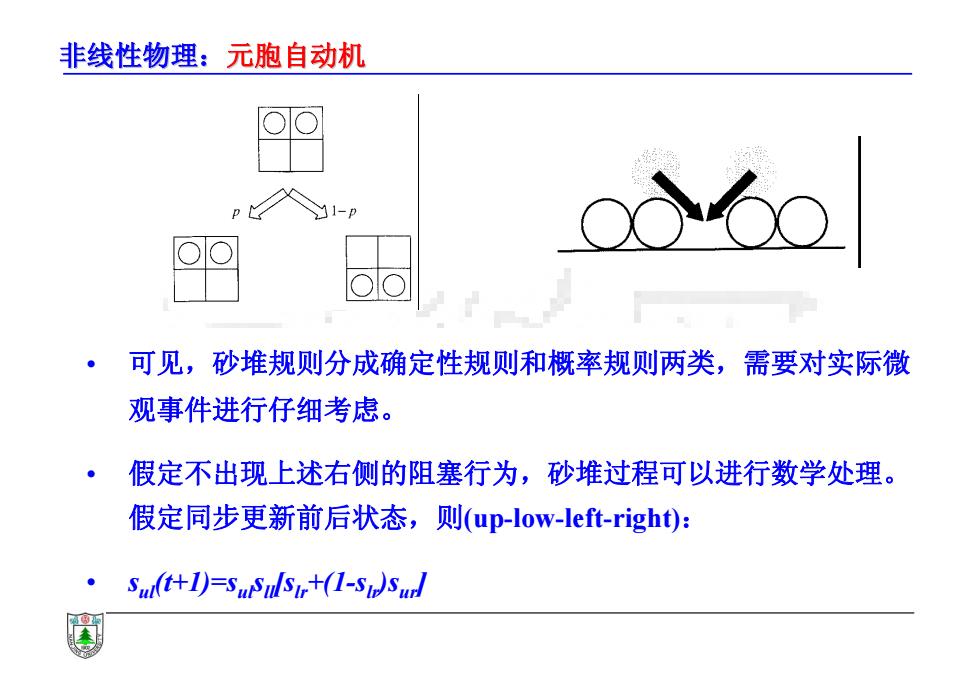
非线性物理:元胞自动机 • 可见,砂堆规则分成确定性规则和概率规则两类,需要对实际微 观事件进行仔细考虑。 • 假定不出现上述右侧的阻塞行为,砂堆过程可以进行数学处理。 假定同步更新前后状态,则(up-low-left-right): • sul(t+1)=sulsll[slr+(1-slr)sur]

非线性物理:元胞自动机 ·Sut什l)=SuSulSir+I-SSu/ ·Sut什)=SurSuSi+(I-SuSull ·Sut什l)=St(I-Sdsu+I-SuSur/ Si(t+1)=Sir+(1-SiSur+(I-SuSuSul ·上述演化过程粒子是守恒的: S(t什)+su(t件)+St什l)tst什l)=Sul+Sur++stsr 实际过程总有一个基础地面,位于其上的砂粒保持静止。以g一1 表示地面,其它位置g=0。则:
非线性物理:元胞自动机 • sul(t+1)=sulsll[slr+(1-slr)sur] • sur(t+1)=surslr[sll+(1-sll)sul] • sll(t+1)=sll+(1-sll)[sul+(1-sur)surslr] • slr(t+1)=slr+(1-slr)[sur+(1-sul)sulsll] • 上述演化过程粒子是守恒的: • sul(t+1)+sur(t+1)+sll(t+1)+slr(t+1)=sul+sur+sll+slr • 实际过程总有一个基础地面,位于其上的砂粒保持静止。以g=1 表示地面,其它位置g=0。则:

非线性物理:元胞自动机 ·Sut什)=SuSu(I-gu小SuSulSir+(I-Ssu/ Sur(t+1)-gurSur+(1-guSurSiSu+(1-SnSull ”St什l)=St(I-SDIS-gu+(I-SuS(1-8uDSd Si(t+1)=Sir+(I-SISur(1-gu+(1-SuSuR1-guDSul ·按照上述规则模拟,得到: ·更为实际的模拟只要通过摸索砂堆规则就可 以做到。这里不再啰嗦
非线性物理:元胞自动机 • sul(t+1)=gulsul+(1-gul)sulsll[slr+(1-slr)sur] • sur(t+1)=gursur+(1-gur)surslr[sll+(1-sll)sul] • sll(t+1)=sll+(1-sll)[sul(1-gul)+(1-sur)sur(1-gur)slr] • slr(t+1)=slr+(1-slr)[sur(1-gur)+(1-sul)sul(1-gul)sll] • 按照上述规则模拟,得到: • 更为实际的模拟只要通过摸索砂堆规则就可 以做到。这里不再啰嗦

非线性物理:元胞自动机 简单系统模拟:蚂蚁规则 蚂蚁规则是Langton等提出的,并非针对真正的蚂蚁运动,只是 作为一个例子显示简单规则如何导致复杂性。 ·基本规则如下:蚂蚁在网格上运动,格位为0或者1,如果运动遇 到0则左转90度并将该格位改成1;如果遇到1则右转并将格位改 成0。初始网格全白。看看,多简单的规则。 ·运动规则经历了初始过渡后进入混沌,然后突然进入一种有序道 路上,规规矩矩地走路了。 ·结论:有微观规则,未必能解释宏观行为。规则重要但不完备
非线性物理:元胞自动机 简单系统模拟:蚂蚁规则 • 蚂蚁规则是Langton等提出的,并非针对真正的蚂蚁运动,只是 作为一个例子显示简单规则如何导致复杂性。 • 基本规则如下:蚂蚁在网格上运动,格位为0或者1,如果运动遇 到0则左转90度并将该格位改成1;如果遇到1则右转并将格位改 成0。初始网格全白。看看,多简单的规则。 • 运动规则经历了初始过渡后进入混沌,然后突然进入一种有序道 路上,规规矩矩地走路了。 • 结论:有微观规则,未必能解释宏观行为。规则重要但不完备

非线性物理:元胞自动机 ·单个蚂蚁:
非线性物理:元胞自动机 • 单个蚂蚁:

非线性物理:元胞自动机 ·两个蚂蚁:
非线性物理:元胞自动机 • 两个蚂蚁:

非线性物理:元胞自动机 ·多个蚂蚁:
非线性物理:元胞自动机 • 多个蚂蚁:

非线性物理:元胞自动机 简单系统模拟:Penrose拼盘三色问题 Penrose拼盘问题是纯数学几何问题,但是对于解释准晶现象做出 了重大贡献。 Penrose:拼盘填满的图形一定是非周期的,即不满足平移对称性等 周期对称操作。 需要解决的问题是如何用三种颜色为三类Penrose拼盘着色,使得 每一种颜色都各自分开,不能通过线边相邻,但是点接触可以。 Penrose拼盘有三类。 From Mark McClure
非线性物理:元胞自动机 简单系统模拟:Penrose拼盘三色问题 • Penrose拼盘问题是纯数学几何问题,但是对于解释准晶现象做出 了重大贡献。 • Penrose拼盘填满的图形一定是非周期的,即不满足平移对称性等 周期对称操作。 • 需要解决的问题是如何用三种颜色为三类Penrose拼盘着色,使得 每一种颜色都各自分开,不能通过线边相邻,但是点接触可以。 • Penrose拼盘有三类。 From Mark McClure
非线性物理:元胞自动机 一类是kites and darts,其中x是黄金分割数,因此每个夹角都 是πl5的整数倍。拼接时要求Kite与Kite相接,Dart与Dart相接, 而且每每要同边相接。 The Kite The Dart
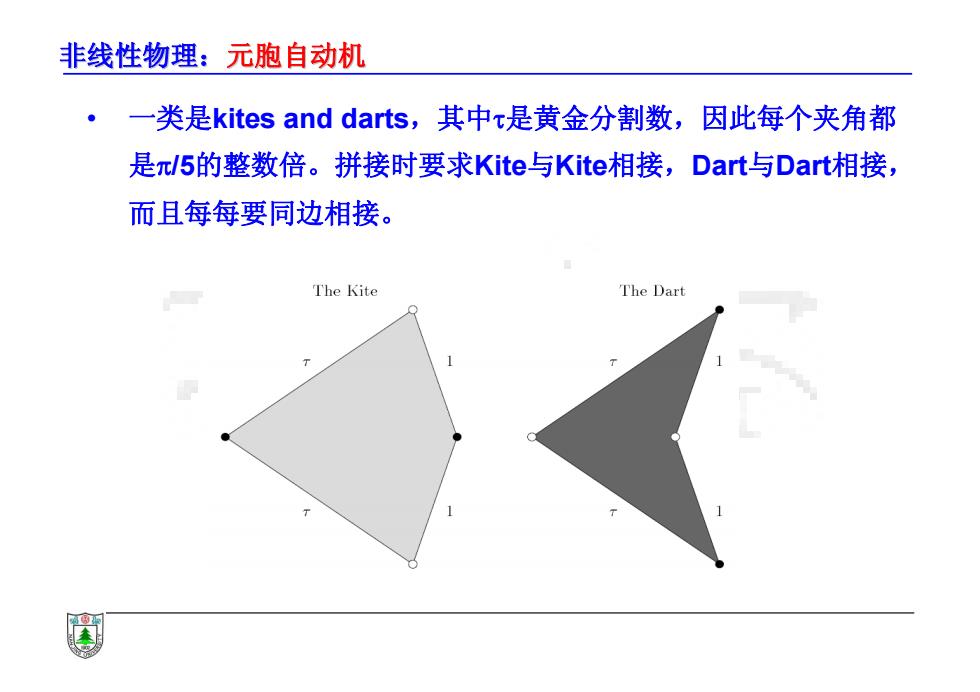
非线性物理:元胞自动机 • 一类是kites and darts,其中是黄金分割数,因此每个夹角都 是/5的整数倍。拼接时要求Kite与Kite相接,Dart与Dart相接, 而且每每要同边相接