
非线性物理:元胞自动机 简单系统模拟:Q2R规则 Q2R规则是Vichniac在1984年针对完全封闭二维类Ising模型元胞 自动机提出来的,体系与外界没有能量交换。 。g 针对一维正方晶格,s=0or1,自旋平行排列交互作用为-J,相 反时为J。每个自旋在并联同时即时必须满足能量不变规则。 ·这一条件不易满足,因为一个自旋翻转会影响其近邻。如: 时刻t:0一10—0一1一0—0一1一10=3J 时刻t+1:0一1—1一1一1一1一1000=-5J 可以看到,这种同时翻转导致系统能量变化了。怎么办?
非线性物理:元胞自动机 简单系统模拟:Q2R规则 • Q2R规则是Vichniac在1984 年针对完全封闭二维类Ising模型元胞 自动机提出来的,体系与外界没有能量交换。 • 针对一维正方晶格,si=0 or 1,自旋平行排列交互作用为-J,相 反时为J。每个自旋在并联同时flip时必须满足能量不变规则。 • 这一条件不易满足,因为一个自旋翻转会影响其近邻。如: • 时刻 t: 0—1—0—0—1—0—0—1—1—0=3J • 时刻t+1: 0—1—1—1—1—1—1—0—0—0=-5J • 可以看到,这种同时翻转导致系统能量变化了。怎么办?

非线性物理:元胞自动机 ·办法是分两步进行,这已经违反元胞自动机的规则了。可见法律 是可以改变的。 ·先固定偶数位自旋,按规则翻转奇数位自旋;再固定奇数位自旋 ,翻转偶数位自旋。如左侧按位置0计(每一步都不能改变能量): ·时刻t: 0-1—0-0—10-0—1-1—0=3J ·时刻什1/2:0一101一1一10—0-1一0=2J固定偶数位 时刻+1:.0一10一1一1一1一10一1一0=3J固定奇数位 可以看到,t时刻的能量与什1时刻能量相同。 挺好玩吧!
非线性物理:元胞自动机 • 办法是分两步进行,这已经违反元胞自动机的规则了。可见法律 是可以改变的。 • 先固定偶数位自旋,按规则翻转奇数位自旋;再固定奇数位自旋 ,翻转偶数位自旋。如左侧按位置0计(每一步都不能改变能量): • 时刻 t: 0—1—0—0—1—0—0—1—1—0=3J • 时刻t+1/2: 0—1—0—1—1—1—0—0—1—0=2J 固定偶数位 • 时刻t+1: 0—1—0—1—1—1—1—0—1—0=3J 固定奇数位 • 可以看到,t时刻的能量与t+1时刻能量相同。 • 挺好玩吧!

非线性物理:元胞自动机 。 对于二维或者高维,采取同样方法。还可以推广到Pots模型及其 它模型。例如,对于二维晶格,另外定义奇偶点阵b=0or1, 自旋翻转只发生在b=1的格点,因此有: S件)=1-S0ifb0=1且(Sws+w5t5+=2;否则 st什)=S。同时,bt什)=1-b)。 ·利用这种元胞自动机规则同样可以研究sig模型的一切性质。 。 问题是这种奇偶代数在动力学演化空间中不是各态历经的。存在 的问题是模拟未必能够得到体系整体能量最低状态。例如下列闭 合一维链:1001()→1100(t+1)-→0110(t+2)→0011(t+3)→1001(t+4) ,满足能量守恒,但是0111也是同样能量态,却无法被访问
非线性物理:元胞自动机 • 对于二维或者高维,采取同样方法。还可以推广到Potts模型及其 它模型。例如,对于二维晶格,另外定义奇偶点阵bij(t)=0 or 1, 自旋翻转只发生在 bij=1的格点,因此有: • sij(t+1)=1-sij(t) if bij(t)=1且(si-1,j+si+1,j+si,j-1+si,j+1)=2;否则 sij(t+1)=sij(t)。同时,bij(t+1)=1-bij(t)。 • 利用这种元胞自动机规则同样可以研究Ising模型的一切性质。 • 问题是这种奇偶代数在动力学演化空间中不是各态历经的。存在 的问题是模拟未必能够得到体系整体能量最低状态。例如下列闭 合一维链:1001(t)1100(t+1)0110(t+2)0011(t+3)1001(t+4) ,满足能量守恒,但是0111也是同样能量态,却无法被访问

非线性物理:元胞自动机 简单系统模拟:退火规则 如果点阵状态离散,例如s=0或1,退火规则的意思是说一个格位 的状态服从其近邻位大多数状态。 ·退火规则中最著名的还是算Vichniac规则。在二维空间,每个格 位的updating决定其Moore邻居状态(S,=0,I)之和: Sum:0123456789 S什:0000101111 与大多数普通规则不同,Sum,)=4,5的两个位置赋值规则作了交 换,从而令人诧异地展示了畴长大过程
非线性物理:元胞自动机 简单系统模拟:退火规则 • 如果点阵状态离散,例如si=0或1,退火规则的意思是说一个格位 的状态服从其近邻位大多数状态。 • 退火规则中最著名的还是算Vichniac规则。在二维空间,每个格 位的updating决定其Moore邻居状态(si=0, 1)之和: • Sumij(t): 0 1 2 3 4 5 6 7 8 9 • sij(t+1): 0 0 0 0 1 0 1 1 1 1 • 与大多数普通规则不同,Sumij(t)=4, 5的两个位置赋值规则作了交 换,从而令人诧异地展示了畴长大过程

非线性物理:元胞自动机
非线性物理:元胞自动机

非线性物理:元胞自动机 简单系统模拟:HPP规则 HPP由Hardy,de Pazzis,.Pomeau.三人在1976年提出的一种规则点 阵方法,来模拟分子动力学过程。格点状态为0o1,表示格点 是否为粒子占据,具有排它性,粒子运动沿格点主方向进行。 PP规则模拟粒子之间弹性碰撞,服从局部动量和能量守恒。但 粒子相互作用演化是完全确定的,过程也是严格时间反演的。 ·格位状态表示为s仁,)=(ESW,东南西北。例如sc,)=(1011)表 示此时有3个粒子沿东、西和北方向进入到此格位。 两个粒子碰撞的表达:(1010)-→(0-10-1),(0101)-→(-10-10)
非线性物理:元胞自动机 简单系统模拟:HPP规则 • HPP由Hardy, de Pazzis, Pomeau三人在1976年提出的一种规则点 阵方法,来模拟分子动力学过程。格点状态为0 or 1,表示格点 是否为粒子占据,具有排它性,粒子运动沿格点主方向进行。 • HPP规则模拟粒子之间弹性碰撞,服从局部动量和能量守恒。但 粒子相互作用演化是完全确定的,过程也是严格时间反演的。 • 格位状态表示为s(r, t)=(ESWN),东南西北。例如s(r, t)=(1011)表 示此时有3个粒子沿东、西和北方向进入到此格位。 • 两个粒子碰撞的表达:(1010)(0-10-1), (0101)(-10-10)
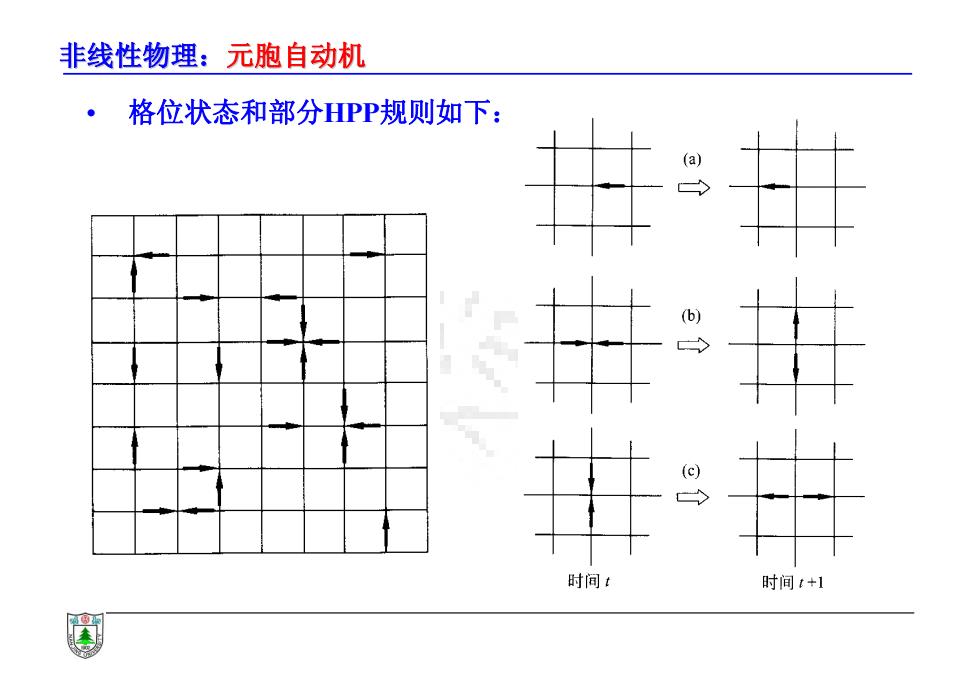
非线性物理:元胞自动机 ·格位状态和部分PP规则如下: 时间t 时间t+1
非线性物理:元胞自动机 • 格位状态和部分HPP规则如下:

非线性物理:元胞自动机 部分演化情况:冲击波问题(有各向异性,与实际不符),改进后 的结果
非线性物理:元胞自动机 • 部分演化情况:冲击波问题(有各向异性,与实际不符),改进后 的结果

非线性物理:元胞自动机 严格的时间反演对称性:
非线性物理:元胞自动机 • 严格的时间反演对称性:

非线性物理:元胞自动机 ·时间反演对称性破缺(右边只有一个粒子位置与左边不同):
非线性物理:元胞自动机 • 时间反演对称性破缺(右边只有一个粒子位置与左边不同):