
非线性物理:分形物理 标度对称性:分数维布朗运动 标度对称性是分形体重要的性质,它反映了分形结构的多尺度性 和自相似性。通过一些熟悉的物理过程还可分析此标度对称性。 ·从随机布朗运动开始。分子平均位移方差和自相关系数: (x)x1 Rfx)=≤小x1+z> =e7 · R(是指数函数,T为特征时间。R(的傅立叶变换就是布朗运动 的功率谱S0: Sf)=DR(r小edrf-
非线性物理:分形物理 标度对称性:分数维布朗运动 • 标度对称性是分形体重要的性质,它反映了分形结构的多尺度性 和自相似性。通过一些熟悉的物理过程还可分析此标度对称性。 • 从随机布朗运动开始。分子平均位移方差和自相关系数: • R()是指数函数,T为特征时间。R()的傅立叶变换就是布朗运动 的功率谱 S(f):

非线性物理:分形物理 。 S0属于噪声宽带谱,所以布朗运动也是褐色噪声。 如果有一噪声信号x,其傅立叶变换为x(f),则: )=」if小ed 2π ·功率谱S)就是其变换系数模的平方: S(f)=(f)a f- ·对布朗运动,指数2。上式微分一次得: (if )d dt 2π
非线性物理:分形物理 • S(f)属于噪声宽带谱,所以布朗运动也是褐色噪声。 • 如果有一噪声信号 x(t),其傅立叶变换为 ,则: • 功率谱 S(f)就是其变换系数模的平方: • 对布朗运动,指数 =2。上式微分一次得:
非线性物理:分形物理 对应的功率谱S0满足: Sfe=旅fxf?=f 对另外一类布朗运动,S0~f”,即白噪声,它可以产生于布朗运 动微分。一般噪声的功率谱指数B∈0,2引。 S(f】 ◆褐色噪声(或11f2噪声) 白噪声 w.e w (c)褐色噪声 (a)白噪声
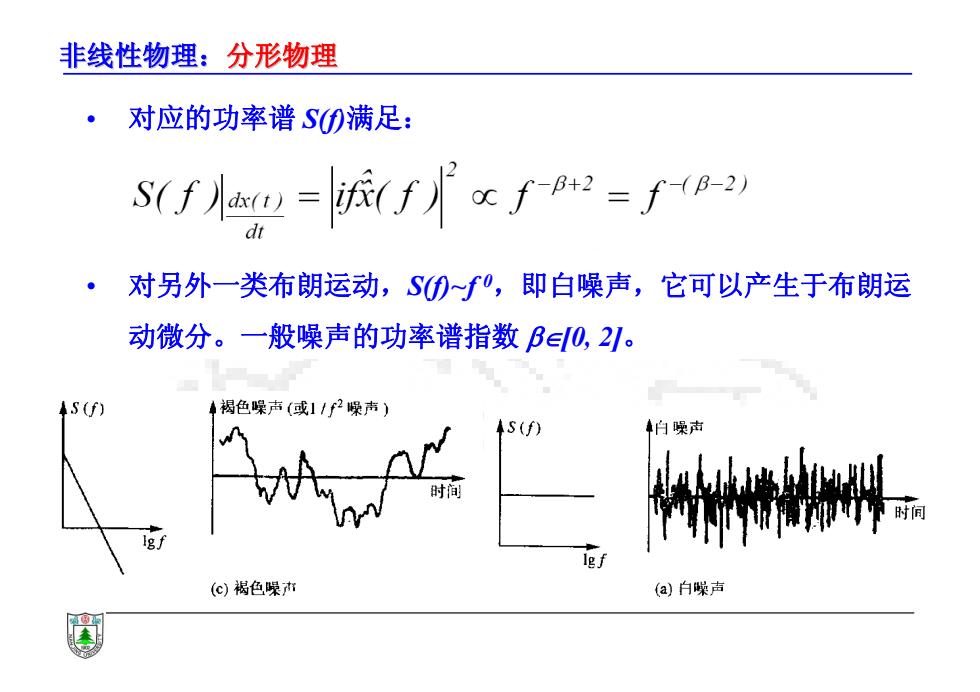
非线性物理:分形物理 • 对应的功率谱 S(f)满足: • 对另外一类布朗运动,S(f)~f 0,即白噪声,它可以产生于布朗运 动微分。一般噪声的功率谱指数 [0, 2]
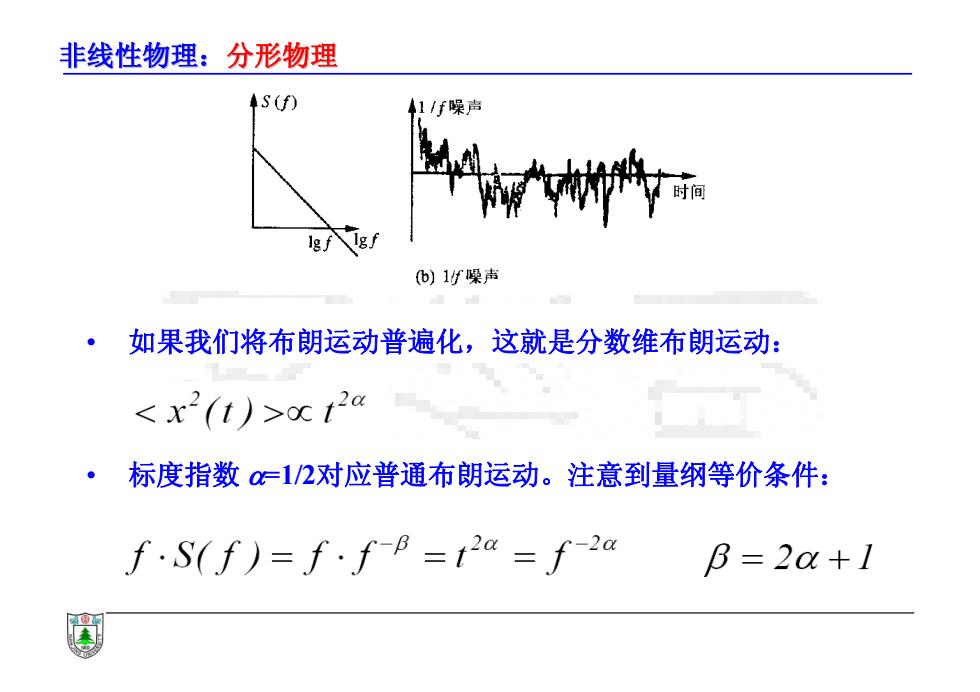
非线性物理:分形物理 ◆S(f) 41f噪声 产p g (b)1f噪声 ·如果我们将布朗运动普遍化,这就是分数维布朗运动: a12a ·标度指数1/2对应普通布朗运动。注意到量纲等价条件: f.S(f)=f·fB=12a=f2a B=2a+1
非线性物理:分形物理 • 如果我们将布朗运动普遍化,这就是分数维布朗运动: • 标度指数 =1/2对应普通布朗运动。注意到量纲等价条件:

非线性物理:分形物理 。 任意随机信号也可以表示为: x(t)octa x(t) in statistical sense x(At 28 上式证明很简单,但是表示了将原有信号的自变量t改变入倍, 则对应的振幅也要改变入倍,则信号彼此在统计上没有差别。 这就是标度不变性和自相似性
非线性物理:分形物理 • 任意随机信号也可以表示为: • 上式证明很简单,但是表示了将原有信号的自变量 t 改变 倍, 则对应的振幅也要改变 - 倍,则信号彼此在统计上没有差别。 这就是标度不变性和自相似性
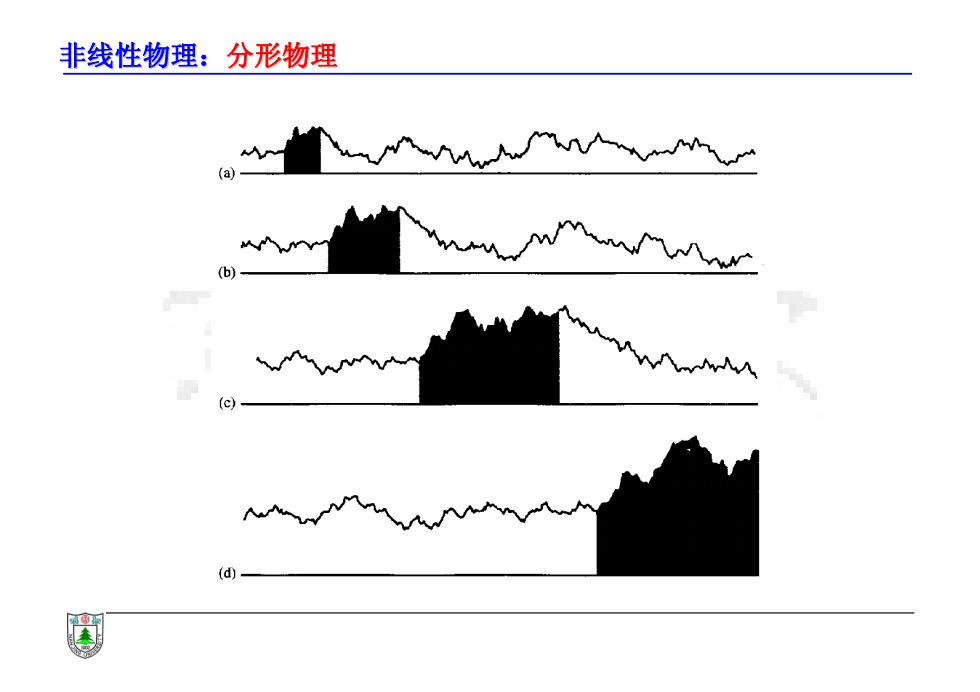
非线性物理:分形物理 (b) (c) (d)
非线性物理:分形物理

非线性物理:分形物理 以普通布朗运动为例说明其分维:因为x()和x(2)/2a自相似, 对t∈0,W区间,用尺度r去测量得到N个单元N=1/m)。 现在用尺度r2去测量t∈0,1/2区间内单元个数。因为指数标度的 缘故,t∈/0,1/2/区间内单元数变成t∈0,1/区间内单元数的1/2倍 ,再用r/2的尺度去测量,就会测得2N/2个单元。 对t∈1/2,1W区间也是一样,总共在t∈0,1区间测得22-N个单元。 依此类推,用尺度2测量,得到22yN个单元,维数D是: D=me-,-a B=2a+1=22-D)+1=5-2D
非线性物理:分形物理 • 以普通布朗运动为例说明其分维:因为 x(t) 和 x(2t)/2 自相似, 对 t[0,1]区间,用尺度 r 去测量得到 N 个单元(N=1/r)。 • 现在用尺度 r/2 去测量t[0,1/2]区间内单元个数。因为指数标度的 缘故, t[0,1/2]区间内单元数变成t[0,1]区间内单元数的1/2倍 , 再用 r/2 的尺度去测量,就会测得 2N/2个单元。 • 对t[1/2,1]区间也是一样,总共在t[0,1]区间测得22-N个单元。 • 依此类推,用尺度 r/2k 测量,得到(22-)kN个单元,维数D是:

非线性物理:分形物理 标度对称性:物理学实例 ·临界现象中的标度不变性: a(T-T) 5[(T-T1=入(T-T) 湍流体系中,相距为r的两点速度差)是随机信号, Kolmogorov证明: Av(r)a ra,a=- 3 B=2C+1 ((Av(r))cr3,s(k)k
非线性物理:分形物理 标度对称性:物理学实例 • 临界现象中的标度不变性: • 湍流体系中,相距为 r 的两点速度差 v(r) 是随机信号, Kolmogorov证明:

非线性物理:分形物理 。 对于湍流,标度不变性也是成立的: ()x(《arP% S(k)元3S(k》 ·对于双变量体系,幂指数标度不变性也成立。以布朗运动为例, x()的概率分布满足: px(i)1)= 2Vπ ·作变换后得到: 1 1 1 x→2x,t→tp(元2x,t)=元2p(x,t)
非线性物理:分形物理 • 对于湍流,标度不变性也是成立的: • 对于双变量体系,幂指数标度不变性也成立。以布朗运动为例, x(t)的概率分布满足: • 作变换后得到:

非线性物理:分形物理 1 1 p(x.t )dx=p(x d()=1 上式说明标度变换能够保持体系许多本征性质不变。 再一个双变量体系是铁磁相变。自由能f是温度t和外场的函 数,作如下变化可得到重整化标度不变性: t→t,h→hf't,2h)=f(t,h) 1 f(t,h)=haF 、hP
非线性物理:分形物理 • 上式说明标度变换能够保持体系许多本征性质不变。 • 再一个双变量体系是铁磁相变。自由能 f 是温度 t 和外场 h 的函 数,作如下变化可得到重整化标度不变性: