
非线性物理:元胞自动机 从最简单开始: 考虑Pascal三角形,也就是杨辉三角形了。 0 10.. 1 ..0110.. 121 ...01210. 1331 013310..」 146?1 .0146410.. ·简单说,三要素:形态pattern,演化规则rule,动力学dynamics 。Pascal三角形的演化规则如下: (a+b)2=a2+2ab+b2, (a+b)3=a3+3a2b+3ab2+b3 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
非线性物理:元胞自动机 从最简单开始: • 考虑Pascal三角形,也就是杨辉三角形了。 • 简单说,三要素:形态pattern,演化规则rule,动力学dynamics 。Pascal三角形的演化规则如下:
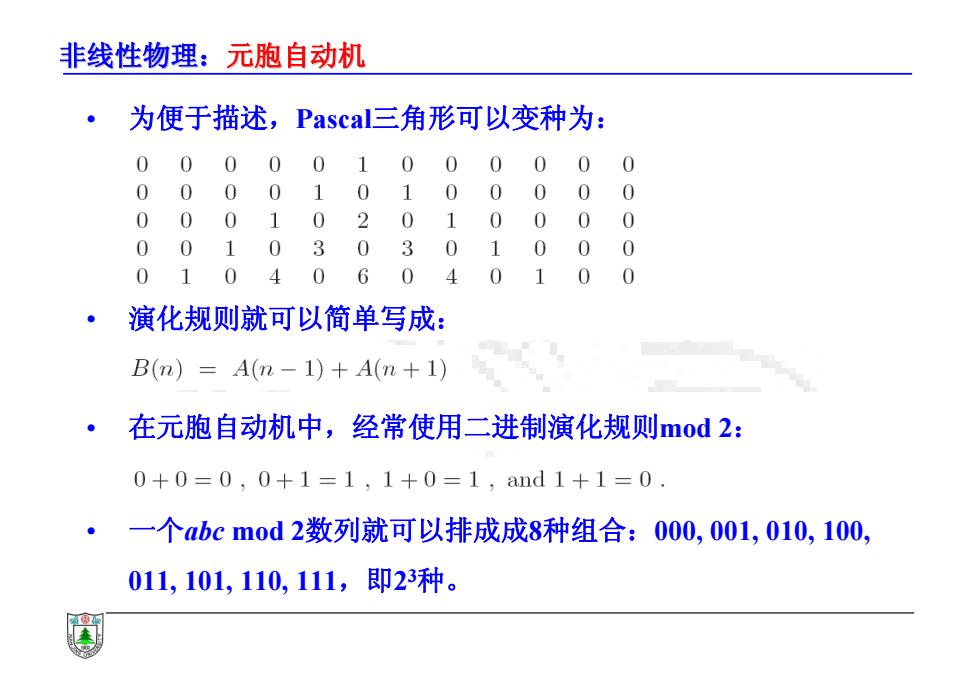
非线性物理:元胞自动机 。 为便于描述,Pascal3三角形可以变种为: 00000100000 0 000010100000 00010201000 0 0 0103030100 0 01040 604 0100 ·演化规则就可以简单写成: B(n)=A(n-1)+A(n+1) 。 在元胞自动机中,经常使用二进制演化规则mod2: 0+0=0,0+1=1,1+0=1,and1+1=0. 一个abcm0d2数列就可以排成成8种组合:000,001,010,100, 011,101,110,111,即23种
非线性物理:元胞自动机 • 为便于描述,Pascal三角形可以变种为: • 演化规则就可以简单写成: • 在元胞自动机中,经常使用二进制演化规则mod 2: • 一个abc mod 2数列就可以排成成8种组合:000, 001, 010, 100, 011, 101, 110, 111,即23种

非线性物理:元胞自动机 ·由此,二进制的Pascal三角形演化规则变成(A为行,B为+1行): 1 if n is odd B(n)=A(n-1)+A(n+1)mod2.A(n)= 0 if n is even ·应用上述规则,Pasca三角形的形态演化图示为: 00000100000
非线性物理:元胞自动机 • 由此,二进制的Pascal三角形演化规则变成(A为i行,B为i+1行): • 应用上述规则,Pascal三角形的形态演化图示为:

非线性物理:元胞自动机 ·就二进制杨辉△作一些游戏作业: (1)按行排列顺序,1的个数是1,2,3,4,5,4,4,8,2,3,3,8,4,8,8,16,2,4,4,8, 那么第50个数是多少? (2)对于第n+1行,1的数目是j个,这里j是此行数n以二进制表示 时的1数目
非线性物理:元胞自动机 • 就二进制杨辉△作一些游戏作业: • (1)按行排列顺序,1的个数是1,2,3,4,5,4,4,8,2,3,3,8,4,8,8,16,2,4,4,8, 那么第50个数是多少? • (2)对于第n+1行,1的数目是2j个,这里j是此行数n以二进制表示 时的1数目

非线性物理:元胞自动机 由Pascal三角形演化作一些推广,就是元胞自动机的雏形了。 给定一个演化规则,改变初始状态,看看演化的结果。注意一维 尺度的影响,是否应用周期边界条件: (a)(..000001001001000000...) (3 ones,3 apart) (b)(..000011001100000000..) (two pairs of ones) (c)(..111000111000111000..) (alternating triples of ones and zeros) (d)(..010001011010001101..) (random》 B(n)=A(n-1)+A(n+1)mod2. 上述规则称为101规则,意即B(n)=A(n-1)+0+A(n+1)
非线性物理:元胞自动机 • 由Pascal三角形演化作一些推广,就是元胞自动机的雏形了。 • 给定一个演化规则,改变初始状态,看看演化的结果。注意一维 尺度的影响,是否应用周期边界条件: • 上述规则称为101规则,意即B(n)=A(n-1)+0+A(n+1)

非线性物理:元胞自动机 或者给定初始状态,看看不同演化规则给出的演化结果。注意一 维尺度的影响,是否应用周期边界条件: B(n)=A(n-1)+A(n)+A(n+1)mod2. (a)(..000001001001000000..)(3ones,3 apart) (b)(..000011001100000000..)(two pairs of ones) (c)(...111000111000111000...)(alternating triples of ones and zeros) (d)(..010001011010001101.)andom) 上述规则成为111规则,意即B(n)=A(n-1)+A()+A(n+1)。 对应地,10101规则:B(n=A(n-2)+0+A(n)+0+A(n+2)
非线性物理:元胞自动机 • 或者给定初始状态,看看不同演化规则给出的演化结果。注意一 维尺度的影响,是否应用周期边界条件: • 上述规则成为111规则,意即B(n)=A(n-1)+A(n)+A(n+1)。 • 对应地,10101规则:B(n)=A(n-2)+0+A(n)+0+A(n+2)

非线性物理:元胞自动机 奇偶规则: ·讨论简单元胞自动机的演化规则,以便给出更严格的定义。 规则虽然简单,但形态却异彩纷呈!例如1970年代Fredkin:提出 的规则体系。 对于二维方格子,一个格位代表一个元胞r),函数)表示其 在t时刻的状态,服从mod2。 44)=卫yr),r'为r四最近临。+)=0,白色;=1,黑色: +)=+1⊕i-1⊕yj+)⊕ywj-1)。1⊕1=0⊕0=0, 1⊕0=0⊕1=1
非线性物理:元胞自动机 奇偶规则: • 讨论简单元胞自动机的演化规则,以便给出更严格的定义。 • 规则虽然简单,但形态却异彩纷呈!例如1970年代Fredkin提出 的规则体系。 • 对于二维方格子,一个格位代表一个元胞r(i,j),函数t(r)表示其 在 t 时刻的状态,服从mod 2。 • t+1(r)=t(r),r 为 r 四最近临。t+1(r)=0,白色;=1,黑色: • t+1(i,j)=t(i+1,j)t(i-1,j)t(i,j+1)t(i,j-1)。11=00=0, 10=01=1

非线性物理:元胞自动机 。 反复使用上述规则可以产生漂亮复杂的图形。 (a) (b) (c) 图1.2在256×256周期性网格上的④规则 (a】为初始构形:(b)和(c)分别为t。=93和t=110迭代后的构形
非线性物理:元胞自动机 • 反复使用上述规则可以产生漂亮复杂的图形

非线性物理:元胞自动机
非线性物理:元胞自动机

非线性物理:元胞自动机 这种演化有一个有趣的性质:迭代2次时,初始图形有可能被复 制;当点阵L=2时,L2次迭代导致初始元胞状态消失。 图形复制示于下图: Cellular Automata 妻 (a) (b) (c) 图1.3当迭代次数为2时,⊕规则复制任意初始图形 (a)表示时间t=0的初始图形;(b)和(c)表示时间t=16和t=t+32相继迭代的图形
非线性物理:元胞自动机 • 这种演化有一个有趣的性质:迭代2n次时,初始图形有可能被复 制;当点阵L=2n时,L/2次迭代导致初始元胞状态消失。 • 图形复制示于下图: