
非线性物理:孤波物理 物理学中的孤子: 孤波是物理世界中混沌的对立面,驱动与耗散竞争产生混沌,也 可以产生孤波。 ·已经有相当数量的非线性微分方程存在孤子解。与此同时,也在 若干物理现象中发现了孤波行为。 F.Calogero和A.Degasperisi在“Spectral Transform and Solitons'” (1982)一书中给出了四十多个具有孤波严格解的微分方程。 ·此处列出几个物理中的孤波效应
非线性物理:孤波物理 物理学中的孤子: • 孤波是物理世界中混沌的对立面,驱动与耗散竞争产生混沌,也 可以产生孤波。 • 已经有相当数量的非线性微分方程存在孤子解。与此同时,也在 若干物理现象中发现了孤波行为。 • F. Calogero和A. Degasperis在“Spectral Transform and Solitons” (1982)一书中给出了四十多个具有孤波严格解的微分方程。 • 此处列出几个物理中的孤波效应

非线性物理:孤波物理 time=2 tIme=0 time=4 time=4
非线性物理:孤波物理

非线性物理:孤波物理 ()KV方程:描述弱非线性与弱色散现象,如浅水波、固体中 热脉冲、纵向弹性色散波的传播、等离子体的离子声波等等: 4,±6ux+4ar=0 ·(2)非线性薛定谔NLS方程:描述弱非线性与强色散现象,如单模 光纤中的光孤子、一维海森堡磁体、电介质中强激光的自聚焦、 流体力学中的涡旋: i4,+ux±2uu=0
非线性物理:孤波物理 • (1) KdV方程:描述弱非线性与弱色散现象,如浅水波、固体中 热脉冲、纵向弹性色散波的传播、等离子体的离子-声波等等: • (2) 非线性薛定谔NLS方程:描述弱非线性与强色散现象,如单模 光纤中的光孤子、一维海森堡磁体、电介质中强激光的自聚焦、 流体力学中的涡旋:

非线性物理:孤波物理 3)sine-Gordon(SG)方程:描述如电荷密度波、自旋密度波、约 瑟夫逊结中的磁通量子、超离子导体、位错传播、铁磁体Bloch 畴壁、自旋传播等现象: ur±sinW=O,u≡u(5,t》 un-uxx+sinu =0,u=ulx,t) (4)p4方程:描述一维晶体的位移相变,是场论模型方程,因为 哈密顿K含有p4而得名。 Puxx+=0 k-3(gi+0i)-3o+io
非线性物理:孤波物理 • (3) sine-Gordon (SG)方程:描述如电荷密度波、自旋密度波、约 瑟夫逊结中的磁通量子、超离子导体、位错传播、铁磁体Bloch 畴壁、自旋传播等现象: • (4) 4 方程:描述一维晶体的位移相变,是场论模型方程,因为 哈密顿 K 含有 4 而得名

非线性物理:孤波物理 (⑤)Double sine-Gordon(DSG)方程:描述He中的B相,原子共振 跃迁等等现象: =0 ·上述(3)(⑤)同属于Kein-Gordon方程的特例,它可以表示为下述 一般形式: 4n-ua=F(u》 F(四=in()时为SG方程,F(=pp3时为p方程, F(=sin(⑩+in(/2)/时为DSG方程
非线性物理:孤波物理 • (5) Double sine-Gordon (DSG)方程:描述3He中的B相,原子共振 跃迁等等现象: • 上述(3)~(5)同属于Klein-Gordon方程的特例, 它可以表示为下述 一般形式: • F(u)=sin(u)时为SG方程,F(u)=-3时为4方程, F(u)=[sin(u)+sin(u/2)]时为DSG方程

非线性物理:孤波物理 孤子的基本性质: ·大致分析一下形成孤子的物理条件。先看微分方程: un a'us,x0 ·这是通常的弦振动方程,线性无色散,为任意函数,通解为: u fx+at)+g(x-at) g(-a表示t=0时波形gx的波 g(x-at) 在t时刻向右平移a距离,即右 行波;而f在+表示左行波
非线性物理:孤波物理 孤子的基本性质: • 大致分析一下形成孤子的物理条件。先看微分方程: • 这是通常的弦振动方程,线性无色散,u为任意函数,通解为: • g(x-at)表示t=0时波形g(x)的波 在t时刻向右平移at距离,即右 行波;而f(x+at)表示左行波

非线性物理:孤波物理 ·这一方程没有什么实际物理,相比较看微分方程: u,+uxe=0 也是线性方程,但是包含色散项4,其通解为: u(x,t)=expli(kx-ot) u(x,t=∑Cexpli(kx-ot刀 o为圆频率,k=2π九为波数,为波长,Fk3,相速为ok=k2与k 有关,即所谓色散。所以通解应该是求和表达式
非线性物理:孤波物理 • 这一方程没有什么实际物理,相比较看微分方程: • 也是线性方程,但是包含色散项uxxx,其通解为: • 为圆频率,k=2/为波数,为波长,=k3,相速为/k=k2与k 有关,即所谓色散。所以通解应该是求和表达式
非线性物理:孤波物理 再考虑一个非线性但是无色散的微分方程: u,+uu,=0 uw为非线性项,行波解是u=uc-v且波速=u,意即波形上不同 高度点的速度不同,波速与高度成正比,因此波形在传播过程中 一定发生变化: (大 w小 1=0 >0
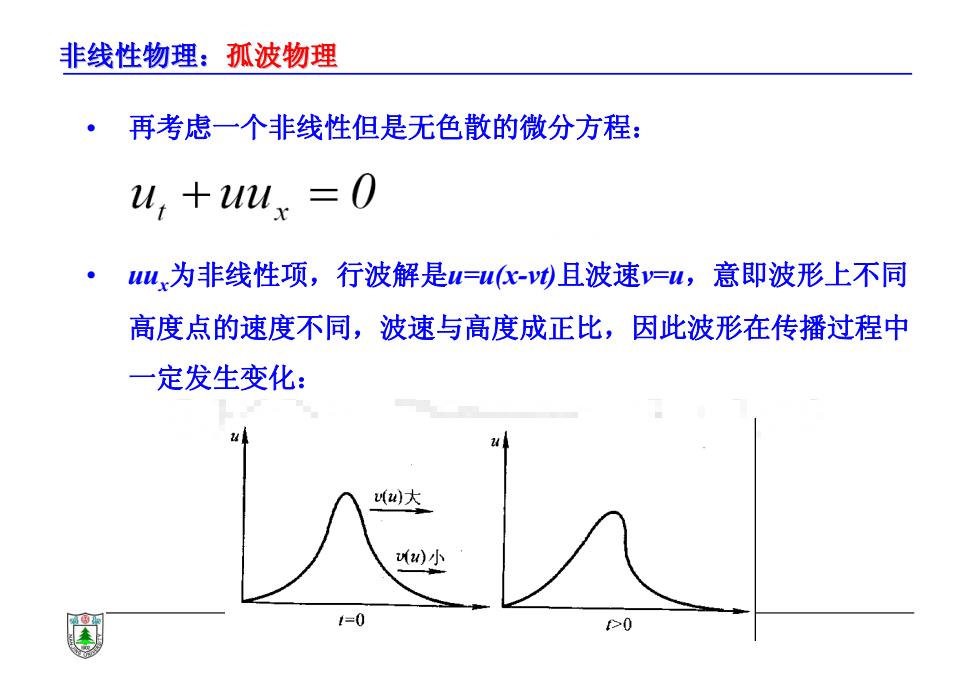
非线性物理:孤波物理 • 再考虑一个非线性但是无色散的微分方程: • uux为非线性项,行波解是u=u(x-vt)且波速v=u,意即波形上不同 高度点的速度不同,波速与高度成正比,因此波形在传播过程中 一定发生变化:
非线性物理:孤波物理 最后考虑KdV方程: u:ouux +ux0 4x为色散项,6uw为非线性项,两者相互抵消,得到孤波解: u(x,t)=-2k'sech'fk(x-4kt-x) 可见波幅与波速关联,导致波幅高 者波速大,典型孤波特征。 ·产生孤子的物理条件:色散与非线 性共存并微妙竞争
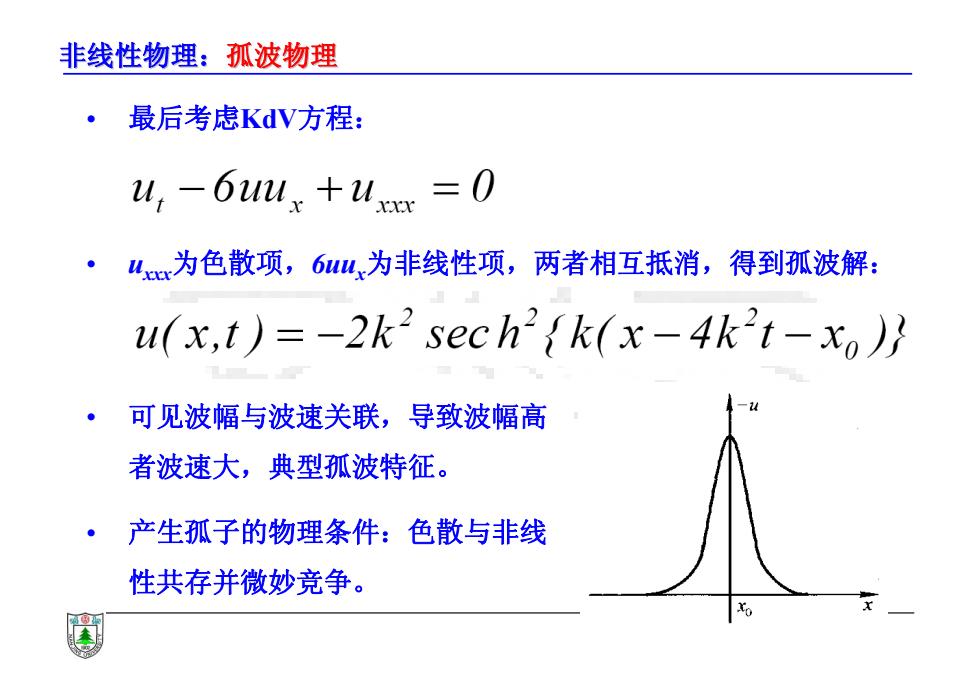
非线性物理:孤波物理 • 最后考虑KdV方程: • uxxx为色散项,6uux为非线性项,两者相互抵消,得到孤波解: • 可见波幅与波速关联,导致波幅高 者波速大,典型孤波特征。 • 产生孤子的物理条件:色散与非线 性共存并微妙竞争
非线性物理:孤波物理 孤子代表的物理过程有一些共同的性质: ()能量有限,且分布在有限的空间范围内。 (2)弹性碰撞。 孤波在传播过程中不会弥散,而波包会弥散。冲击波波形前段是 奇异的,也不是孤波。 波 冲击波
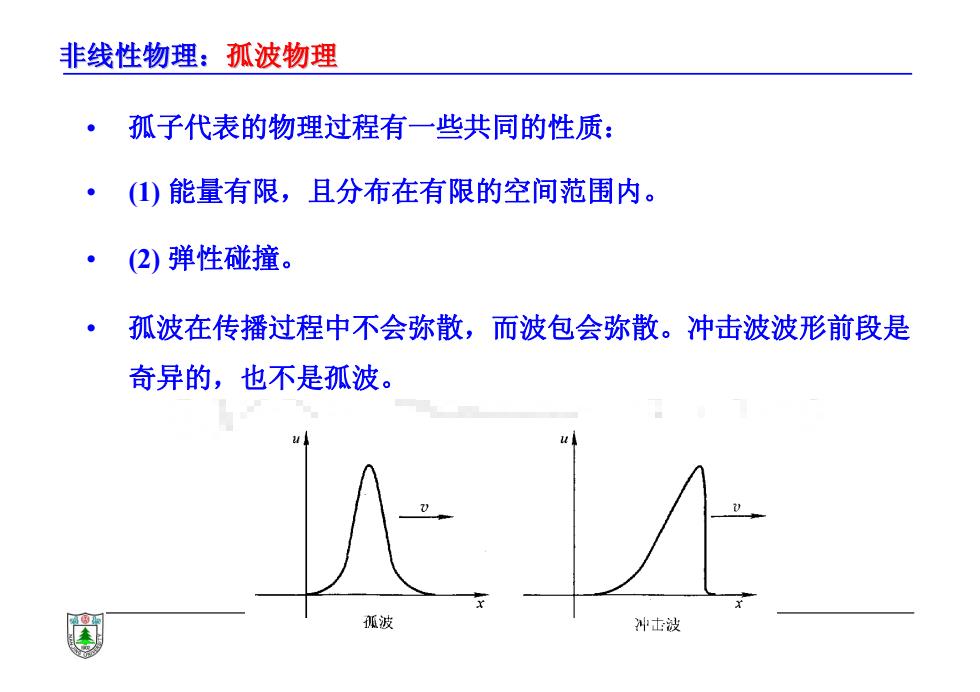
非线性物理:孤波物理 • 孤子代表的物理过程有一些共同的性质: • (1) 能量有限,且分布在有限的空间范围内。 • (2) 弹性碰撞。 • 孤波在传播过程中不会弥散,而波包会弥散。冲击波波形前段是 奇异的,也不是孤波