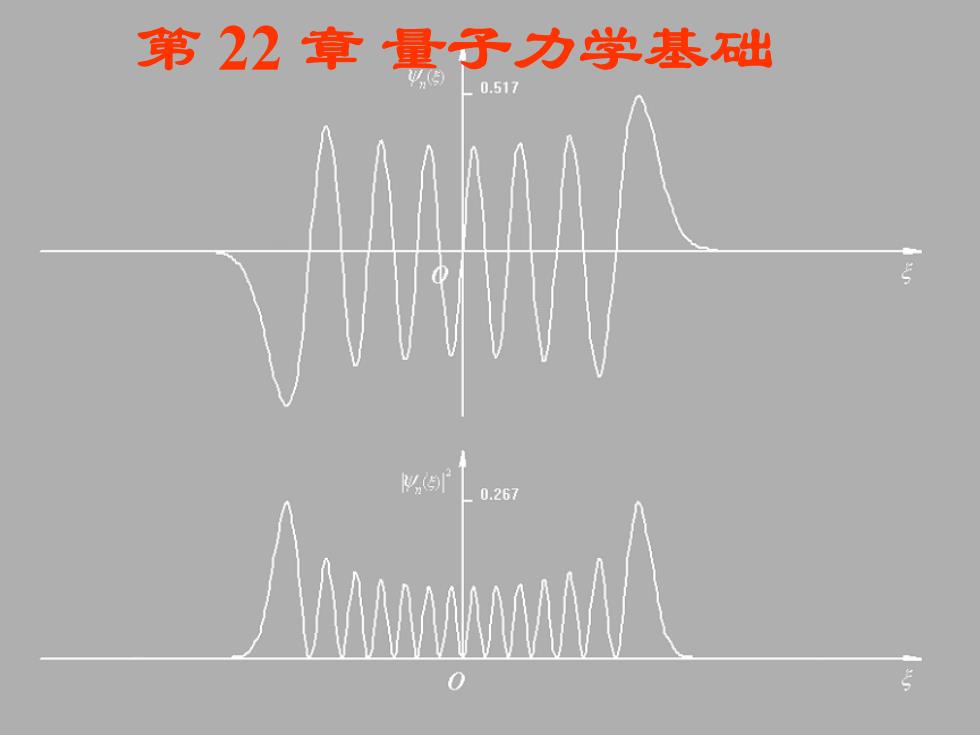
第22章量子力学基出 0.517 0.267
第 22 章 量子力学基础

第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.1实物粒子的波动性 光具有波粒二象性,那么实物粒子是否也应具有 波粒二象性?或实物粒子具有波动性吗? 一、 德布罗意物质波假设 德布罗意(L.V.de Broglie 1892一1986,法国)从光具 有波粒二象性出发,认为实 物粒子也应具有波动性。 1924年11月在巴黎大学提交的博士论文中提出: “我们因而倾向于假定,任何运动物体都伴随着一个 波动,而且不可能把物体的运动跟波的传播拆开
光具有波粒二象性,那么实物粒子是否也应具有 波粒二象性?或实物粒子具有波动性吗? 一、 德布罗意物质波假设 德布罗意(L.V. de Broglie 1892—1986,法国 )从光具 有波粒二象性出发,认为实 物粒子也应具有波动性。 1924 年11月在巴黎大学提交的博士论文中提出: §22.1 实物粒子的波动性 “我们因而倾向于假定,任何运动物体都伴随着一个 波动,而且不可能把物体的运动跟波的传播拆开。

具有能量E和动量D的实物粒子所联系的波的频率v 和波长入有关系: E=hv h 这种波既不是机械波也不是电磁波,称为物质波或德 布罗意波。 在答辩会上有人问:“这种波怎样用实验来证实呢?” 德布罗意答:“可以从电子在晶体上散射这样的实验 中检查到这样的波
这种波既不是机械波也不是电磁波,称为物质波或德 布罗意波。 = hE ν 具有能量 E和动量p的实物粒子所联系的波的频率 ν 和波长 λ有关系: p h λ = 在答辩会上有人问: “这种波怎样用实验来证实呢? ” 德布罗意答: “可以从电子在晶体上散射这样的实验 中检查到这样的波。

朗之万把德布罗意的文章寄给爱因斯坦,爱因斯坦说: “揭开了自然界巨大帷幕的一角”。 “瞧瞧吧,看来疯狂,可真是站得住脚呢”。 尽管此假说的真伪有待实验检验,但爱因斯坦还是推荐 德布罗意取得了博士学位。 虽然后来的实验验证由戴维孙和革末完成了,但当时 纯粹是理论推测。 [例22-1刂估算:m=1g,=1cm/s的实物粒子的波长 h=h=6.62×104 p mv 10-3x10-2=6.62×10-29m 粒子对应的波长太小,波动性无法表现出来!
虽然后来的实验验证由戴维孙和革末完成了,但当时 纯粹是理论推测。 朗之万把德布罗意的文章寄给爱因斯坦,爱因斯坦说: “揭开了自然界巨大帷幕的一角”。 “瞧瞧吧,看来疯狂,可真是站得住脚呢”。 尽管此假说的真伪有待实验检验,但爱因斯坦还是推荐 德布罗意取得了博士学位。 [ 例22-1] 估算 : m=1g ,v=1 cm/s的实物粒子的波长 p h λ = mv h = m1062.6 1010 1062.6 29 23 34 − −− − ×= × × = 粒子对应的波长太小,波动性无法表现出来!

对于电子,=9.1×10-31kg,设加速电压为U 1 mw2=eU→v= 2eU 2 m h = mv ,√2emU 12.25 A UJ=150V→2=1A 相当于晶格常数数量级,通过类似于晶体对X射线的 衍射,可以实现晶体对电子的衍射
对于电子, m= 9.1×10-31 kg,设加速电压为U = eUmv2 2 1 m eU v 2 =⇒ emU h mv h 2 λ == o U λ =⇒= A1V150 o A 25.12 U λ ≈ 相当于晶格常数数量级,通过类似于晶体对X射线的 衍射,可以实现晶体对电子的衍射

[例22-2)德布罗意把物质波假设用于氢原子认为:如 果电子在经典的圆轨道上运动,它对应于一个环形驻 波,满足 2πr=n2,(n=1,2,3,.…) h r=n 2元 2元mv h L=rmy =n 2元 玻尔量子化条件 德布罗意用物质波的概念成功地解释了玻尔提出的 轨道量子化条件
[例22-2] 德布罗意把物质波假设用于氢原子认为:如 果电子在经典的圆轨道上运动,它对应于一个环形驻 波,满足 2π = λ nnr = ),...3,2,1( , 2π λ = nr 2πmv h = n = rmvL 2π h = n ——玻尔量子化条件 德布罗意用物质波的概念成功地解释了玻尔提出的 轨道量子化条件
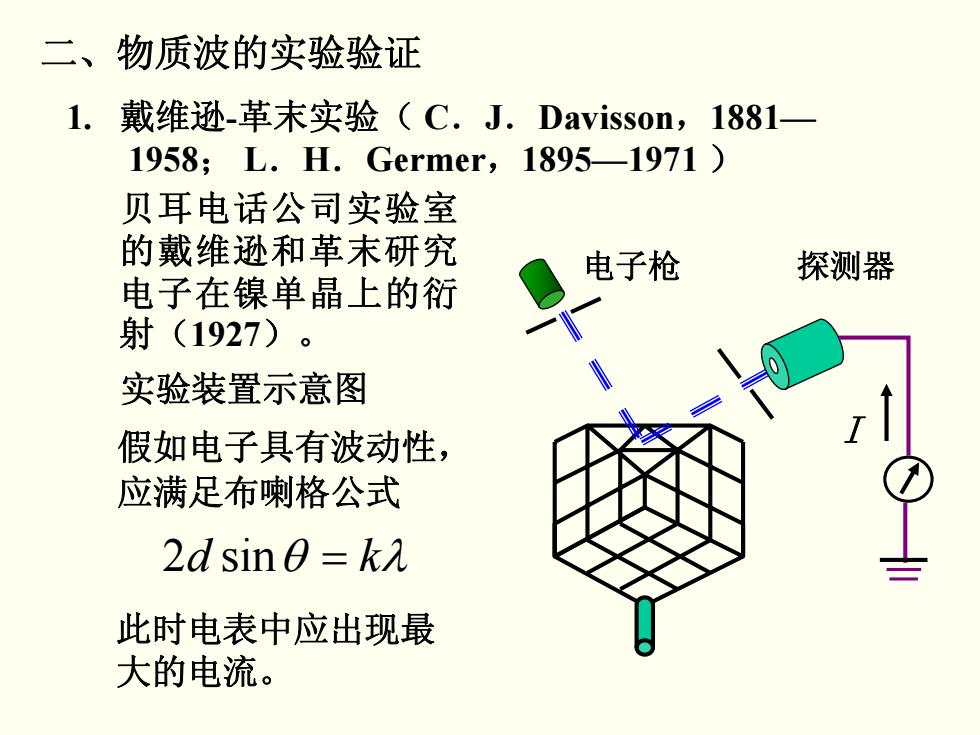
二、物质波的实验验证 1. 戴维逊-革末实验(C.J.Davisson,1881一 1958;L.H.Germer,18951971) 贝耳电话公司实验室 的戴维逊和革末研究 电子枪 探测器 电子在镍单晶上的衍 射(1927)。 实验装置示意图 假如电子具有波动性, 应满足布喇格公式 2dsin0=kλ 此时电表中应出现最 大的电流
二、物质波的实验验证 贝耳电话公司实验室 的戴维逊和革末研究 电子在镍单晶上的衍 射(1927)。 电子枪 1. 戴维逊 -革末实验( C.J.Davisson ,1881— 1958; L.H.Germer ,1895—1971 ) 实验装置示意图 假如电子具有波动性, 应满足布喇格公式 sin2 θ = kd λ 此时电表中应出现最 大的电流。 探测器 I

12.25 2dsin0=k U k=1,2,3,…) U=k 12.25 2d sin0 12.25 12.25 2× 3x- 12.25 2d sin0 2d sin0 2d sin 0 若固定0角,改变加速电压,会多次出现电流极大
θ d 若固定θ 角,改变加速电压,会多次出现电流极大。 (k = ,3,2,1 L) U kd 25.12 sin2 θ = sin2 θ 25.12 d = kU ,... sin2 25.12 3 , sin2 25.12 2 , sin2 25.12d θ d θ d θ = × ×
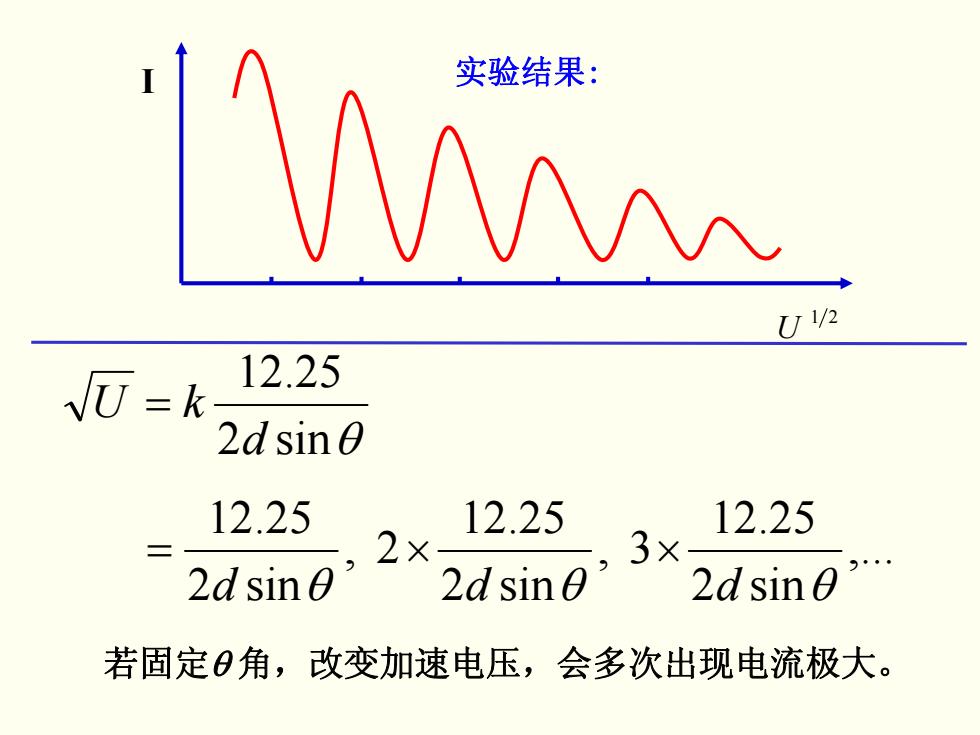
实验结果: U/2 √U=k 12.25 2dsin0 12.25 12.25 12.25 2× 3× 2d sin0 2d sin0 2d sin 0 若固定0角,改变加速电压,会多次出现电流极大
sin2 θ 25.12 d = kU ,... sin2 25.12 3 , sin2 25.12 2 , sin2 25.12d θ d θ d θ = × × 若固定θ 角,改变加速电压,会多次出现电流极大。 21 U I 实验结果: