
第21章量子光学基出 §21.0引言 §21.1热辐射黑体辐射 §21.2普朗克的能量子假说和黑体辐射公式 §21.3光的粒子性 §21.4康普顿散射 §21.5氢原子光谱 Bohr理论 §21.6光的辐射和吸收 §21.7激光
第 21 章 量子光学基础 §21.1 热辐射 黑体辐射 §21.2 普朗克的能量子假说和黑体辐射公式 §21.3 光的粒子性 §21.4 康普顿散射 §21.5 氢原子光谱 Bohr 理论 §21.6 光的辐射和吸收 §21.7 激光 §21.0 引言

§21.1热辐射黑体辐射 一、 基尔霍夫定律(Kirchhoff) 1.热辐射的基本概念 所有物体在任何温度下都要发射电磁 波,这种与温度有关的辐射称为热辐射 (heat radiation). 热辐射的电磁波的波长、强度与物体的温 度有关,还与物体的性质表面形状有关
所有物体在任何温度下都要发射 所有物体在任何温度下都要发射电磁 波,这种与温度有关的辐射称为 这种与温度有关的辐射称为热辐射 (heat radiation) (heat radiation) 。 热辐射的电磁波的波长、强度与物体的温 热辐射的电磁波的波长、强度与物体的温 度有关,还与物体的性质表面形状有关。 度有关,还与物体的性质表面形状有关。 §21.1 热辐射 黑体辐射 1. 热辐射的基本概念 热辐射的基本概念 一、基尔霍夫定律(Kirchhoff) (Kirchhoff)

单色辐出度M2:为了描述物体在温度为T时辐射能 量的能力,定义物体单位表面在单位时间内发出的波 长在入附近单位波长间隔内的电磁波的能量为单色辐 出度M2,即 M,(T)= dE d入 辐出度M():物体从单位面积上发射的所有各种波 长的辐射总功率称为物体的总辐出度M(T) M(T)=M(T)da 0
单色辐出度Mλ : 为了描述物体在温度为 为了描述物体在温度为 T 时辐射能 量的能力,定义物体单位表面在单位时间内发出的波 物体单位表面在单位时间内发出的波 长在λ附近单位波长间隔内的电磁波的能量为 附近单位波长间隔内的电磁波的能量为单色辐 出度Mλ,即 辐出度 M(T): 物体从单位面积上发射的所有各种波 物体从单位面积上发射的所有各种波 长的辐射总功率称为物体的总辐出度 长的辐射总功率称为物体的总辐出度 M(T) λ λ λ d d )( E TM = ∫ ∞ = 0 λ TMTM d)()( λ

吸收比:当辐射从外界入射到物体表面时,吸收能 量与入射总能量之比: E吸收 0(T)= E入射 吸收能力的量度 单色吸收比:当辐射从外界入射到物体表面时,在 2到2+d2的波段内吸收的能量“E吸收d2”与入射的 总能量“E,入射d2”之比: 0x(2,T)= E吸牧 E公
入射 吸收 E E α T )( = 单色吸收比: 当辐射从外界入射到物体表面时,在 当辐射从外界入射到物体表面时,在 λ到λ+dλ的波段内吸收的能量 的波段内吸收的能量 “ Eλ吸收 dλ”与入射的 总能量“ Eλ入射 dλ”之比: 吸收比: 当辐射从外界入射到物体表面时, 当辐射从外界入射到物体表面时,吸收能 量与入射总能量之比 量与入射总能量之比: 吸收能力的量度 吸收能力的量度 入射 吸收 λ λ λα E E T ),( =

2.基尔霍夫定律 同一个物体的发射本领和吸收本领有内在联 系。 基尔霍夫定律:实验发现,在温度一定时物体 在某波长入处的单色辐出度与单色吸收比的比 值与物体及其物体表面的性质无关,即 M,(2,T) M3(九,T) =…=M(2,T) a(元,T)a2(2,T)
同一个物体的发射本领和吸收本领有内在联 同一个物体的发射本领和吸收本领有内在联 系。 2. 基尔霍夫定律 基尔霍夫定律: 基尔霍夫定律:实验发现,在温度一定时物体 实验发现,在温度一定时物体 在某波长 λ处的单色辐出度与单色吸收比的比 处的单色辐出度与单色吸收比的比 值与物体及其物体表面的性质无关,即 值与物体及其物体表面的性质无关,即 ),( ),( ),( ),( ),( 0 2 2 1 1 TM T TM T TM λ λα λ λα λ = L ==
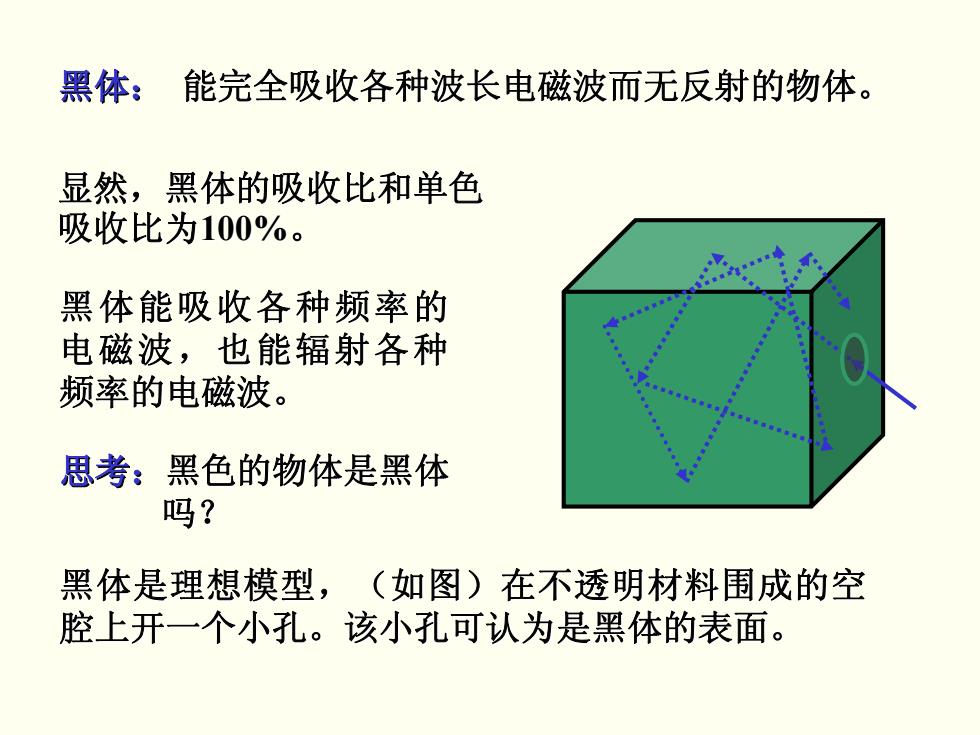
黑体: 能完全吸收各种波长电磁波而无反射的物体。 显然,黑体的吸收比和单色 吸收比为100%。 黑体能吸收各种频率的 电磁波,也能辐射各种 频率的电磁波。 思考:黑色的物体是黑体 吗? 黑体是理想模型,(如图)在不透明材料围成的空 腔上开一个小孔。该小孔可认为是黑体的表面
黑体: 能完全吸收各种波长电磁波而无反射的物体。 能完全吸收各种波长电磁波而无反射的物体。 显然,黑体的吸收比和单色 吸收比为100%。 黑体是理想模型,( 黑体是理想模型,(如图)在不透明材料围成的空 如图)在不透明材料围成的空 腔上开一个小孔。该小孔可认为是黑体的表面。 一个小孔。该小孔可认为是黑体的表面。 黑体能吸收各种频率的 黑体能吸收各种频率的 电磁波,也能辐射各种 电磁波,也能辐射各种 频率的电磁波。 频率的电磁波。 思考:黑色的物体是黑体 黑色的物体是黑体 吗?

二 黑体辐射的基本规律 M/(1010 W/m) 实验规律发现: 70 在温度一定时 60 2200K 黑体的单色辐 出度与波长有 50 关,并存在 一 2000K 40以 极大值,所对 应的极值点九m 30 1800K 有关系 20 1600K T个→↓ 10 上述全波段的黑体辐射 2.0 3.0/m 规律是基于以下几个实 图21-2 验规律逐步建立的:
二、 黑体辐射的基本规律 实验规律发现: 实验规律发现: λ m T λm ↓↑→ 在温度一定时 黑体的单色辐 出度与波长有 关,并存在一 极大值,所对 应的极值点 λ m 有关系 上述全波段的黑体辐射 上述全波段的黑体辐射 规律是基于以下几个实 规律是基于以下几个实 验规律逐步建立的: 验规律逐步建立的:

L.斯特藩一玻耳兹曼定律(J.Stefan&L.Boltzmann) 实验证明,黑体的总辐出度M(T)(每条曲 线下的面积)与温度的四次方成正比 M(T)=oT o=5.67X108W/(m2K4)一Stefan恒量
1. 斯特藩—玻耳兹曼定律( 玻耳兹曼定律(J. Stefan & L. Boltzmann J. Stefan & L. Boltzmann) σ =5.67×10- 8 W/(m2K4)—— Stefan 恒量。 4 )( = σTTM 实验证明,黑体的总辐出度 实验证明,黑体的总辐出度M0(T)(每条曲 线下的面积)与温度的四次方成正比 与温度的四次方成正比

2.维恩位移定律(W.Wien) 黑体辐射中单色辐出度的极值 波长2m与黑体温度T之积为常 数 T九m=b 其中b=2.898×103mK为 Wien常数。 以上两个实验定律是遥感、高温测量和红外追踪等 技术的物理基础
2. 维恩位移定律(W. Wien W. Wien) 黑体辐射中单色辐出度的极值 黑体辐射中单色辐出度的极值 波长λ m与黑体温度T 之积为常 数 其中b= 2.898 = 2.898×10-3 m·K 为 Wien 常数。 λ m = bT 以上两个实验定律是 以上两个实验定律是遥感、高温测量和红外追踪等 技术的物理基础。 技术的物理基础

3.维恩公式(非前面的维恩位移定律) 假定电磁波能量分布服从类似于经典的麦克斯韦速 度分布律,可得 M(T)=v3eBv7 式中、B为常量。 4.瑞利一金斯公式 瑞利一金斯从经典的能量均分定理出发,得到 M(T) 2vk灯 c2 式中k为波耳兹曼常量
3. 维恩公式(非前面的维恩位移定律) 维恩公式(非前面的维恩位移定律) 4. 瑞利—金斯公式 ( ) T TM /3e βν ν αν − = ( ) kT c TM 2 3 2πν ν = 瑞利—金斯从经典的能量均分定理出发,得到 经典的能量均分定理出发,得到 式中 k 为波耳兹曼常量。 为波耳兹曼常量。 假定电磁波能量分布服从类似于经典的麦克斯韦速 假定电磁波能量分布服从类似于经典的麦克斯韦速 度分布律,可得 度分布律,可得 式中α、β为常量